A rope passess over a pulley which is sufficiently high . Two monkeys of equel mass climb the rope from opposite ends , one of them climbing quickly than the other , relative to the rope . Assuming that the pulley and the rope are weightless and the rope is in extensible , which of monkeys will reach the top first?
Both will reach the top at the same time because the length of the two segments of the rope on the two sides of the pulley are always equal.
Similar Questions
A rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View SolutionA rope thrown over a pulley has a on one of its ends and a counterbalancing mass M on its other end. The man whose mass is m, climbs upwards by →△r relative to the ladder and then stops. Ignoring masses of the pulley and the rope, as well as the friction the pulley axis, find the displacement of the centre of mass of this system.
View Solution
Knowledge Check
A rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
AmMvrBm2MvrCMmvrD2MmvrTwo persons of equal weight are hanging by their hands from the ends of a rope hung over a frictionless pulley. They begin to climb the rope. One person can climb twice the speed of the other (with respect to the tope) Who will get to the top first?
AThe faster climberBThe slower climberCBoth will get to the top simultaneouslyDNothing can be said as it is indeterminateAs shown in figure a monkey of 20g mass is holding a light rope that passes over a frictionless pulley. A bunch of bananas of the same mass is tied to the other end of rope. Inorder to get access to the bunch the monkey starts climbing the rope. The distance between the monkey and the bananas is
 ADecreasingBIncreasingCUnchangedDNothing can be stated
ADecreasingBIncreasingCUnchangedDNothing can be stated
A rope thrown over a pulley has a on one of its ends and a counterbalancing mass M on its other end. The man whose mass is m, climbs upwards by →△r relative to the ladder and then stops. Ignoring masses of the pulley and the rope, as well as the friction the pulley axis, find the displacement of the centre of mass of this system.
View SolutionA light rope is passed over a pulley such that at its one end a block is attached , and on the other end a boy is climbing up with acceleration g2 relative to rope. Mass of the block is 30 kg and that of the boy is 40 kg. Find the tension and acceleration of the rope .
View SolutionA light rope is passed over a pulley such that at its one end a block is attached , and on the other end a boy is climbing up with acceleration g2 relative to rope. Mass of the block is 30 kg and that of the boy is 40 kg. Find the tension and acceleration of the rope .
View SolutionA monkey is climbing on a rope that goes over a smooth light pulley and supports a block of equal mass at the other end. Show that whatever force the monkey exerts on the rope, the monkey and the block move in the same direction with
View SolutionA Monkey is Climbing on a Rope that Goes Over a Smooth Light Pulley and Supports a Block of Equal Mass at the Other End in the Following
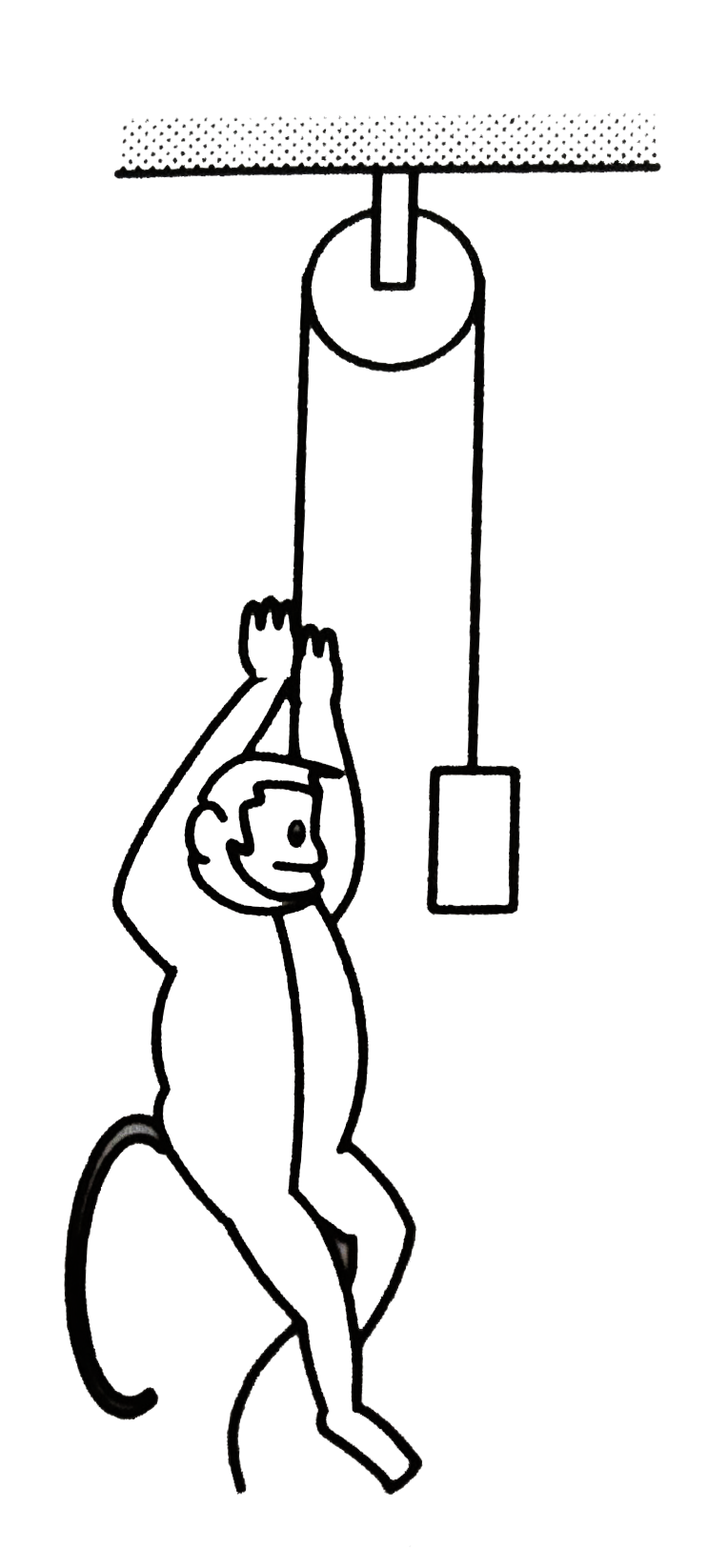
View Solution

