The sum of infinite terms of the series cot−1(22+12)+cot−1(23+122)+cot−1(24+123)+…=cot−1k then k = Solution in Telugu
The correct Answer is:2
Step by step video, text & image solution for The sum of infinite terms of the series cot^(-1)(2^(2)+1/2)+cot^(-1)(2^(3)+1/2^(2))+cot^(-1)(2^(4)+1/2^(3))+…=cot^(-1)k then k = by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INVERSET TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSET TRIGONOMETRIC FUNCTIONSEXERCISE - LECTURE SHEET (EXERCISE -III LEVEL -I (MAIN) SINGLE ANSWER TYPE QUESTIONS)
15 Videos
- INVERSET TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSET TRIGONOMETRIC FUNCTIONSEXERCISE - LECTURE SHEET (EXERCISE -III LEVEL -II (ADVANCED) SINGLE ANSWER TYPE QUESTIONS)1
1 Video
- INVERSET TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSET TRIGONOMETRIC FUNCTIONSEXERCISE - LECTURE SHEET (EXERCISE -II LEVEL -I (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
1 Video
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - PRACTICE EXERCISE
37 Videos
- LIMITSBOOK - AAKASH SERIESCHAPTER - LIMITSEXERCISE - PRACTICE EXERCISE
143 Videos
Similar Questions
The solution set of the equation sin−1x=2tan−1x is
View SolutionThe sum of the solutions of the equation 2sin−1√x2+x+1+cos−1√x2+x=3π2 is
View SolutionLet (x,y) be such that sin−1(ax)+cos−1(y)+cos−1(bxy)=π/2. Match the statements in column I which statements in column II.
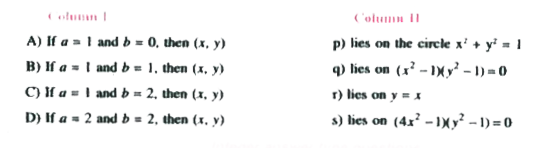
View SolutionThe value of cot−1(cot(5π6))=
View SolutionLtx→0x2−5x+72x2+3x−1=
View SolutionIf the sum of first 16 terms of the series s=cot−1(22+12)+cot−1(23+122)+cot−1(24+123)+ up to terms is cot−1(1+2n2(216−1)) , then find the value of n.
View SolutionThe value of 2(cot^(-1))(1)/(2)-(cot^(-1))(4)/(3) is
View SolutionThe sum to infinite terms of the series cot^(-1)(2^(2)+(1)/(2))+cot^(-1)(2^(3)+(1)/(2^(2)))+cot^(-1)(2^(4)+(1)/(2^(3)))+
View SolutionSum to infinite terms the series: cot−1(12+34)+cot−1(22+34)+cot−1(32+34)+….
View SolutionSum of infinite terms of the series cot−1(12+34)+cot−1(22+34)+cot−1(32+34)+... is
View SolutionFind the sum to n terms of the series Sn=cot−1(22+12)+cot−1(23+122)+cot−1(24+123)+..... upto n terms ?
View SolutionValue of 2cot−112−cot−143is-
View Solution2cot−1.12−cot−1.43 का मान है -
View SolutionThe sum of the infinite series cot−12+cot−18+cot−118+cot−132+..... is equal to
View SolutionSum of infinite terms of the series cot−1(12+34)+cot−1(22+34)+cot−1(32+34)+….. is
View SolutionThe sum of infinite terms of the series cot−1(22+12)+cot−1(23+122)+cot−1(24+123)+…=cot−1k then k =
View Solution

