Two vectors →pand →Q are having their magnitudes in the ratio √3:1. Further ∣∣→P+→Q∣∣=∣∣→P−→Q∣∣, then the angle between the vectors (→P+→Q)and (→P−→Q) is
The correct Answer is:60∘
Topper's Solved these Questions
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER
10 Videos
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - Numerical Exercise( Level 1)
13 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Questions for Descriptive Answers
10 Videos
- EXPANSION OF GASESBOOK - AAKASH SERIESCHAPTER - EXPANSION OF GASESEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
Similar Questions
Find the components of vector →A=2ˆi+3ˆj along the directions of ˆi+ˆj and ˆi−ˆj.
View SolutionDerive the dimensions of Planck.s constant. Which other quantity has simA body of mass 5kg moves under a force of 10ˆi+10ˆj−20ˆk. What is the acceleration produced?
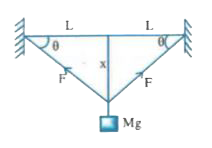
View SolutionA steel wire of area of cross-section A and length 2L is clamped firmly between two points seperated by a distance .2L.. A body is hung from the middle point of the wire such that the middle point sags by a distance X. Calculate the mass of the body and the angle made by the string with the horizontal. (Young.s modulus of Steel = y)
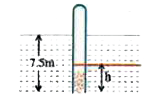
View SolutionA thin uniform tube of length 9 m closed at one end is immersed in water to a depth of 7.5 m. Find the height h to which water rises in the tube. Ignore any temperature change and take atmosphere pressure as 10 mg water column.
View SolutionIf vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
View SolutionIf |vecP + vecQ|= | vecP| -|vecQ| , the angle between the vectors vecP and vecQ is
View Solutionif |vecP + vecQ| = |vecP| + |vecQ| , the angle between the vectors vecP and vecQ is
View SolutionIf |vecP + vecQ| = |vecP -vecQ| the angle between vecP and vecQ is
View Solutionif vecP +vecQ = vecP -vecQ , then
View SolutionMagnitude of resultant of two vectors vecP and vecQ is equal to magnitude of vecP . Find the angle between vecQ and resultant of vec2P and vecQ .
View SolutionIf |vecP+vecQ|=|vecP|+|vecQ| . The angle between the vectors vecPandvecQ is
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P∣∣−∣∣→Q∣∣, the the angle between the vectors →Pand→Q
View SolutionThere vectors vecP, vecQ and vecR are such that vecP+vecQ+vecR=0 Vectors vecP and vecQ are equal in , magnitude . The magnitude of vector vecR is sqrt2 times the magnitude of either vecP or vecQ . Calculate the angle between these vectors .
View SolutionTwo vectors →P and →Q are having their magnitudes in the ratio √3:1.Further।→P+→Q।=।→P−→Q। then the angle between the vectors (→P+→Q) and (→P−→Q) is
View Solution→P+→Q=→P−→Q है
View Solution

