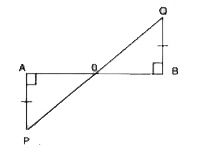
दिए गए आकृति में, AP और BQ रेखाखण्ड AB पर लम्ब है और AP=BQ तो सिद्ध करें कि बिन्दु O रेखाखण्ड AB और PQ का मध्य - बिन्दु है।
The correct Answer is:अतः O, रेखाखण्ड AB और PQ का मध्य-बिन्दु है।
Step by step video, text & image solution for दिए गए आकृति में, AP और BQ रेखाखण्ड AB पर लम्ब है और AP=BQ तो सिद्ध करें कि बिन्दु O रेखाखण्ड AB और PQ का मध्य - बिन्दु है। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023समान प्रश्न
Match the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn the following figure, if O is the center of the circle and ¯¯¯¯¯¯AB is the diameter, then find ∠ACB.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E02_009_Q01.png" width="80%"gt
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solution
