Let f(x)=ax2+bx+c,a,b,c∈Randa≠0 suppose f(x)>0 for all x∈R Let g(x)=f(x)+f(x)+f'(x) thenSolution in Telugu
g(x)>0∀x∈R
g(x)<0∀x∈R
g(x)=0 has no real complex roots
sum of the roots of g(x)=0 is -3 if ω,ω2 are roots of f(x)=0 where ω is the cube roots of unity
The correct Answer is:A, C, D
Step by step video, text & image solution for Let f(x)=ax^(2)+bx+c,a,b,c in Randa ne0 suppose f(x)gt0 for all x in R Let g(x)=f(x)+f(x)+f'(x) then by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAXIMA AND MINIMA Book:AAKASH SERIESChapter:MAXIMA AND MINIMA Exercise:LECTURE SHEET (EXERCISE -II) (MATRIX MATCHING TYPE QUESTIONS)
Explore 3 Videos
- MAXIMA AND MINIMA Book:AAKASH SERIESChapter:MAXIMA AND MINIMA Exercise:LECTURE SHEET (EXERCISE -II) (LINKED COMPREHENSION TYPE QUESTIONS)
Explore 5 Videos
- MAXIMA AND MINIMA Book:AAKASH SERIESChapter:MAXIMA AND MINIMA Exercise:LECTURE SHEET (EXERCISE -II) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
Explore 54 Videos
- MAXIMA & MINIMABook:AAKASH SERIESChapter:MAXIMA & MINIMAExercise:EXERCISE-III
Explore 35 Videos
- MEAN VALUE THEOREMSBook:AAKASH SERIESChapter:MEAN VALUE THEOREMSExercise:PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )
Explore 2 Videos
Similar Questions
Match the max l min value of function in Column I with corresponding values in Column -II

View Solutionf(x) is continous and differentiable function .Given , f(x) assumes valus of the form ±√I where I denotes set of whole numbers whenever x=a or b , otherwise f(x) assumes real values. Also , f(c)=−32and|f(a)|≤|f(b)|
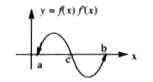
The number of rational values that f(a) +f(b)+f(c ) can assume is /are
View SolutionThe absolute maximum of y=x3−3x+2in0≤x≤2 is
View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )
View SolutionLet a,b,c in R. If f(x)=ax^(2)+bx+c is such that a +b+c=3. If f(x)=ax^(2)+bx+c is such f(x+y)=f(x)+f(y)+xy AA x,y in R then sum_(n=1)^(10)f(n) is equal to
View SolutionLet a,b,c in R. If f(x)=ax^(2)+bx+c and a+b+c=3 and f(x+y)=f(x)+f(y)+xy then sum_(n=1)^(10)f(n) is
View SolutionLet f(x)=ax^(2)+bx+c, where a,b,c in R,a!=0. Suppose |f(x)|<=1,x in[0,1], then
View SolutionA function f(x) is differentiable at x=c(c∈R). Let g(x)=|f(x)|,f(c)=0 then
View SolutionLet f(x) be polynomial function of defree 2 such that f(x)>0 for all x∈R. If g(x)=f(x)+f'(x)+f''(x) for all x, then
View SolutionLet g(x)=f(x)−2{f(x)}2+9{f(x)}3 for all x∈R Then
View SolutionLet f(x)=ax2−bx+c2,b≠0andf(x)≠0 for all x∈R. Then
View SolutionLet f(x)=eaxsin(bx+c)and f''(x)=r2eaxsin(bx+θ),then-
View SolutionLet f(x)=ax2−bx+c2,b≠0andf(x)≠0 for all x∈R. Then
View SolutionLet a fiunction f defined by f(x)=x−|x|xforx≠0 and f(0) =2 then f is
View Solution
