In △ABC, point M is midpoint of side BC. If AB2+AC2=290cm2 and AM=8 cm, find BC.Solution in Marathi
Step by step video & image solution for In triangle ABC, point M is midpoint of side BC. If AB^2+AC^2=290cm^2 and AM=8 cm, find BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Out of the following which is a Pythagorean triplet? a) (1,5,10) b) (3,4,5) c) (2,2,2) d) (5,5,2)
View SolutionWhich number cannot represent a probability? a)23 b)1.5 c)0.15 d)0.7
View SolutionWhich one of the following is a quadratic equation? a)5x−3=x2 b)x(x+5)=2 c)n−1=2n d)1x2(x+2)=x
View Solutionयदि ΔABC की भुजा BC का मध्य बिन्दु D है तब सिद्ध कीजिये कि
AB2+AC2=2(AD2+BD2)
View Solutionएक △ABC में, AB = AC तथा D, AC का मध्य बिंदु है और BC2=AC×CD हो तो सिद्ध कीजिए कि BD = BC
View Solutionत्रिभुज ABC के अंदर एक वृत्त है जो भुजा AB , BC और AC को क्रमशः बिंदु D , E और F पर स्पर्श करती है। अगर AB = 12 सेमी, BC = 8 सेमी और AC = 10 सेमी हो तो AD , BE और CF की लम्बाई ज्ञात करें।
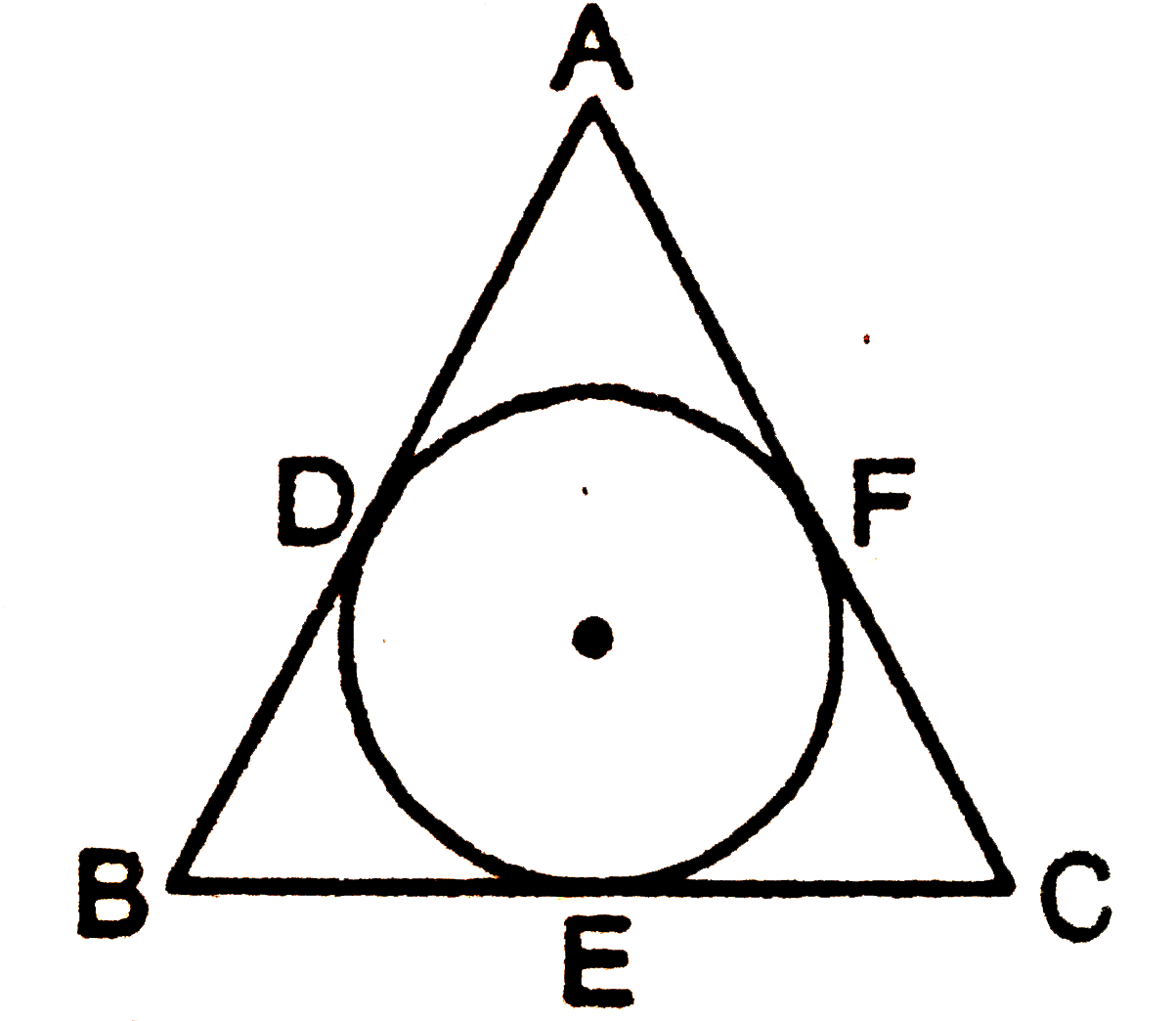
View Solutionयदि O, त्रिभुज ABC के भुजा BC का मध्यबिन्दु है तो दिखाएँ कि
AB2+AC2=2(AD2+BD2).
View Solutionत्रिभुज ABC की भुजाओं AB तथा AC पर क्रमशः बिंदु D तथा E इस प्रकार है की DE∣∣BC है|यदि AD = 2 .4 सेमि., AE =3 .2 सेमि., DE =2 सेमि., तथा BC = 6 सेमि,हो तो BD तथा CE का मान ज्ञात करो|
View SolutionIn ΔABC, point M is the midpoint of BC,AB2+AC2=290cm,AM=8cm,find BC.
View SolutionIn ΔABC, with ∠B=90∘, BC=6 cm and AB=8 cm, D is a point on AC such that AD=2 cm and E is the midpoint of AB. Join D to E and extend it to meet at F. Find BF.
View SolutionIn a triangle ABC the angle A is twice the angle C, the side BC is 2 cm longer than the side AB, and AC=5 cm. Find AB and BC.
View SolutionIn Delta ABC ,point M is midpoint of side BC. If AB^(2) + AC^(2) = 290 cm^(2) = 290 cm ^(@) and AM = 8 cm, find BC.
View SolutionIn ΔABC,AB2+AC2=122andBC=10 Find the length of the median on side BC.
View SolutionDelta ABC In (AB + BC) (AB-BC) = AC^(2) Who
View SolutionIf D is the midpoint of the side BC of a triangle ABC then ¯¯¯¯¯¯AB2+¯¯¯¯¯¯AC2=
View Solution
