In question 3 of the same exercise, the radius of the sphere is a. The length of the string is also a. Find tension in the string.
The correct Answer is:B, C
To find the tension in the string when the radius of the sphere is a and the length of the string is also a, we can follow these steps:
Step 1: Understand the Setup
We have a sphere with radius a and a string of length a attached to it. The sphere is in a position where the string makes an angle of 30∘ with the vertical.
Step 2: Identify Forces Acting on the Sphere
The forces acting on the sphere are:
- The gravitational force mg acting downward.
- The tension T in the string acting at an angle of 30∘ to the vertical.
Step 3: Resolve the Tension into Components
The tension T can be resolved into two components:
- The vertical component Tcos(30∘), which acts upward.
- The horizontal component Tsin(30∘), which acts towards the wall.
Step 4: Apply Equilibrium Conditions
Since the sphere is at rest, the forces must balance:
1. In the vertical direction:
Tcos(30∘)=mg
2. In the horizontal direction:
Tsin(30∘)=N
where N is the normal force exerted by the wall on the sphere.
Step 5: Solve for Tension
From the vertical force balance, we can express T:
T=mgcos(30∘)
We know that cos(30∘)=√32, so:
T=mg√32=2mg√3
Final Answer
Thus, the tension in the string is:
T=2mg√3
We have a sphere with radius a and a string of length a attached to it. The sphere is in a position where the string makes an angle of 30∘ with the vertical.
The forces acting on the sphere are:
- The gravitational force mg acting downward.
- The tension T in the string acting at an angle of 30∘ to the vertical.
The tension T can be resolved into two components:
- The vertical component Tcos(30∘), which acts upward.
- The horizontal component Tsin(30∘), which acts towards the wall.
Since the sphere is at rest, the forces must balance:
1. In the vertical direction:
Tcos(30∘)=mg
2. In the horizontal direction:
Tsin(30∘)=N
where N is the normal force exerted by the wall on the sphere.
From the vertical force balance, we can express T:
T=mgcos(30∘)
We know that cos(30∘)=√32, so:
T=mg√32=2mg√3
Thus, the tension in the string is:
T=2mg√3
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Exercise 8.2
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Exercise 8.3
Explore 8 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Miscellaneous Examples
Explore 9 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
Knowledge Check
In the question number 66, the tension in the string is
A30NB36NC34ND32NForce of friction and tension in a string are
AGravitational forcesBElectromagnetic forcesCNuclear forcesDWeal forces
In the previous question the tension in the string is
View SolutionFor the system shown in figure, the tensions in the string
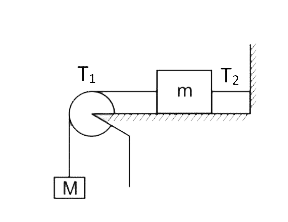
View SolutionIn the arrangement shown, all the surface are smooth, strings and pulleys are light. Find the tension in the string.
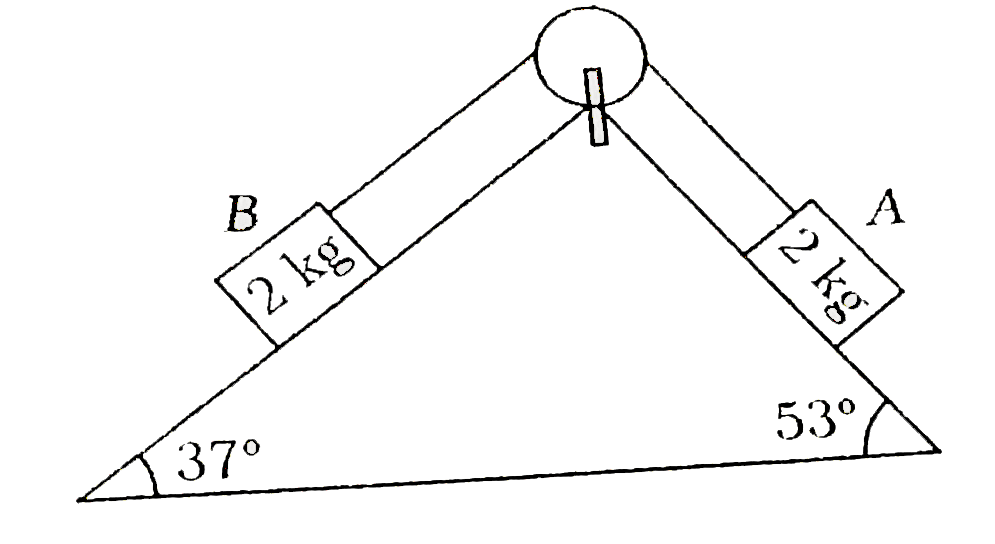
View SolutionDraw the free body diagram of following also find the tension in each string
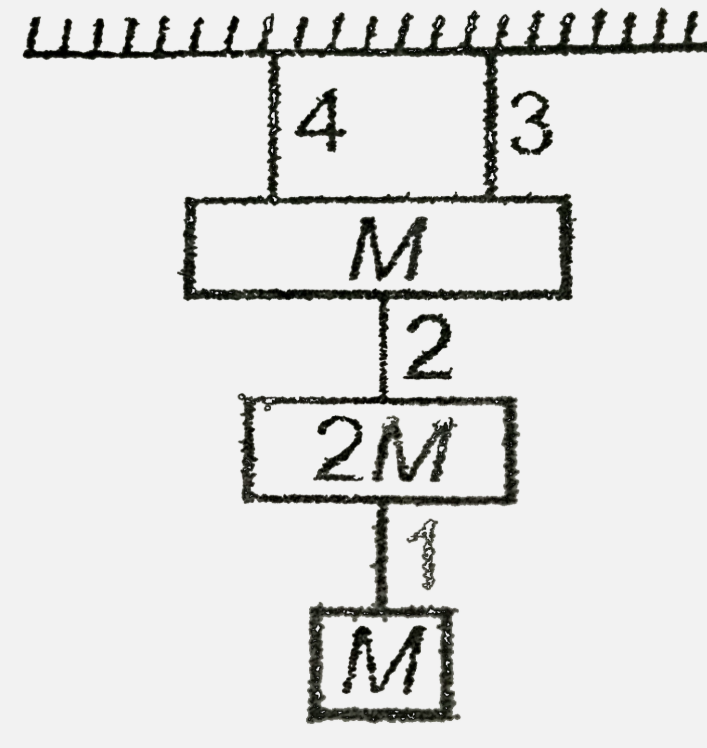
View SolutionA stone is tied to one end of a string and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the length of the string is halved and its angular velocity is doubled , the tension in the string will be
View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

View Solution


