Magnitude of focal length of a spherical mirror is f and magnitude of linear magnification is 12
If image is inverted, it is a concave mirror
If image is erect, it is a convex mirror
Object distance from the mirror may be 3f
Object distance from the mirror may be f.
The correct Answer is:A, B, C, D
To solve the problem, we need to analyze the situation for both types of spherical mirrors: concave and convex. We will use the mirror formula and the magnification formula to derive the object distance and determine the type of mirror based on the given conditions.
1. Understanding the Given Information:
- Magnitude of focal length of a spherical mirror: f
- Magnitude of linear magnification: 12
2. Determine the Type of Mirror:
- If the image is inverted, it indicates a concave mirror.
- If the image is erect, it indicates a convex mirror.
3. Case 1: Convex Mirror
- For a convex mirror, the object distance u is negative, so we can denote it as u=−x.
- The magnification m for a convex mirror is given by:
m=h′h=vu
where v is the image distance. Given m=12, we have:
v−x=12⟹v=−x2
- The focal length f for a convex mirror is positive.
4. Using the Mirror Formula:
- The mirror formula is:
1f=1v+1u
- Substituting the values:
1f=1−x2+1−x
- Simplifying:
1f=−2x−1x=−3x
- Therefore, we get:
f=−x3
- Since f is positive for a convex mirror, this case is valid if x=3f.
5. Case 2: Concave Mirror
- For a concave mirror, the object distance u is again negative, so we denote it as u=−x.
- The image distance v for a concave mirror, given the image is inverted (real), is:
v=−x2
- The focal length f for a concave mirror is negative.
6. Using the Mirror Formula Again:
- Substituting into the mirror formula:
1−f=1−x2+1−x
- Simplifying:
−1f=−2x−1x=−3x
- Therefore:
f=x3
- Since f is negative for a concave mirror, this case is valid if x=3f.
Conclusion:
- If the image is erect, it is a convex mirror with object distance x=f.
- If the image is inverted, it is a concave mirror with object distance x=3f.
Final Answer:
- The statements are correct for both types of mirrors:
- For a convex mirror: Object distance may be f.
- For a concave mirror: Object distance may be 3f.
- Magnitude of focal length of a spherical mirror: f
- Magnitude of linear magnification: 12
- If the image is inverted, it indicates a concave mirror.
- If the image is erect, it indicates a convex mirror.
- For a convex mirror, the object distance u is negative, so we can denote it as u=−x.
- The magnification m for a convex mirror is given by:
m=h′h=vu
where v is the image distance. Given m=12, we have:
v−x=12⟹v=−x2
- The focal length f for a convex mirror is positive.
- The mirror formula is:
1f=1v+1u
- Substituting the values:
1f=1−x2+1−x
- Simplifying:
1f=−2x−1x=−3x
- Therefore, we get:
f=−x3
- Since f is positive for a convex mirror, this case is valid if x=3f.
- For a concave mirror, the object distance u is again negative, so we denote it as u=−x.
- The image distance v for a concave mirror, given the image is inverted (real), is:
v=−x2
- The focal length f for a concave mirror is negative.
- Substituting into the mirror formula:
1−f=1−x2+1−x
- Simplifying:
−1f=−2x−1x=−3x
- Therefore:
f=x3
- Since f is negative for a concave mirror, this case is valid if x=3f.
- If the image is erect, it is a convex mirror with object distance x=f.
- If the image is inverted, it is a concave mirror with object distance x=3f.
- The statements are correct for both types of mirrors:
- For a convex mirror: Object distance may be f.
- For a concave mirror: Object distance may be 3f.
Topper's Solved these Questions
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Level 2 Comprehensive Based
Explore 4 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Level 2 Single Correct
Explore 16 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Medical entrance gallary
Explore 73 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Level 2 Subjective
Explore 21 Videos
Similar Questions
A plane mirror (M1) and a concave mirror (M2) of focal length 10 cm are arranged as shown in figure. An object is kept at origin. Answers the following questions. (consider image formed by single reflection in all cases).
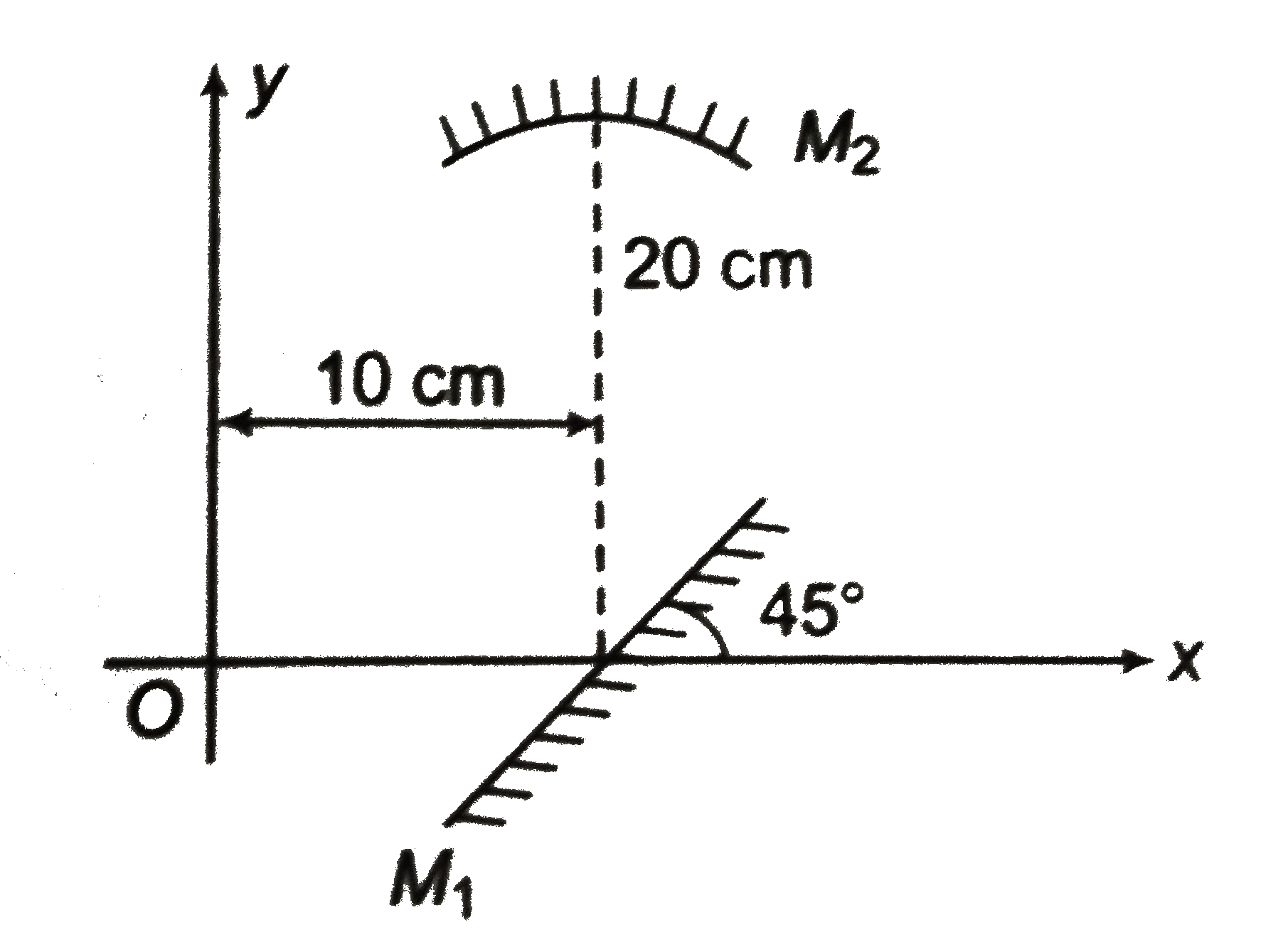
The coordination of image formed by plane mirror are
View SolutionA point source of light S is placed at a distance 10 cm in front of the centre of a mirror of width 20 cm suspended vertically on a wall. An insect walks with a speed 10cm/s in front of the mirror along a line parallel to the mirror at a distance 20 cm from it as shown in figure. find the maximum time during which the insect can see the image of the source S in the mirror.
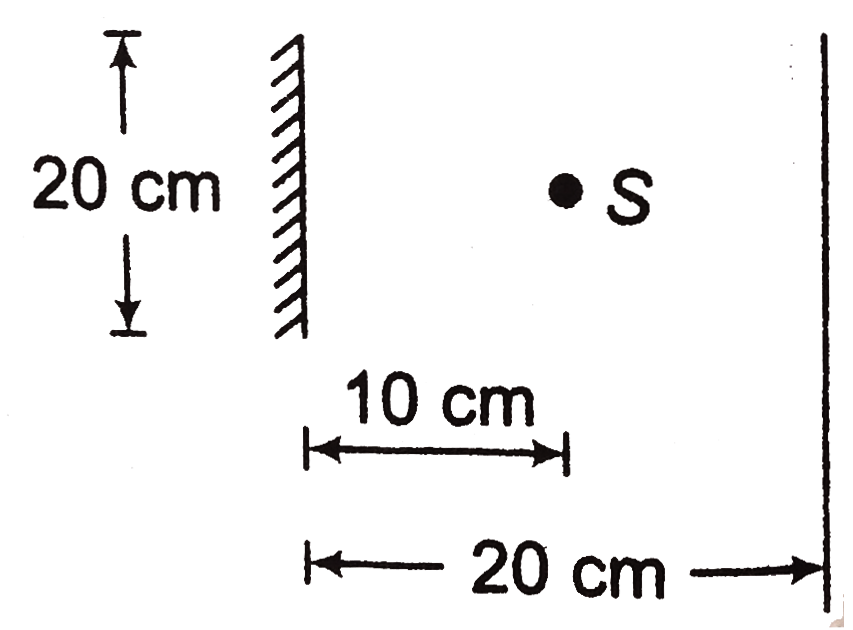
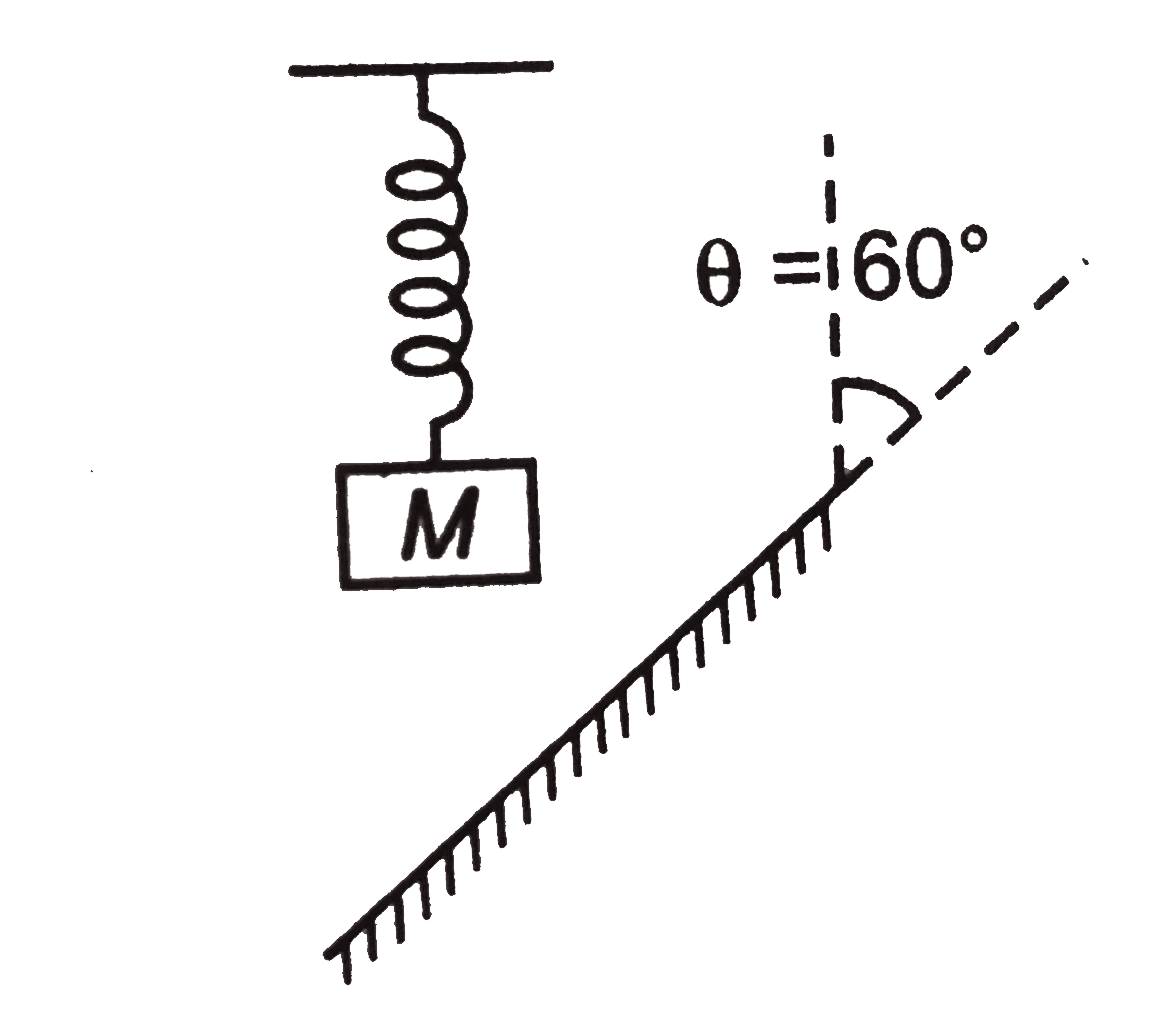
View SolutionAn insect of negligible mass is sitting on a block of mass M, tied with a spring of force cosntant k. The block performs simple harmonic motion with amplitude A in front of aplane mirror as shown, teh maximum speed of insect relative to its image will be
View SolutionTwo identical glass (μg=3/2) equi- convex lenses of focal length f each are kept in contact. The space between the two lenses is also filled with water (μg=4/3). The focal length of the combination is
View Solutiona. Figure (a) shows the optical axis of a lens, the point source of light A, and its virtual image A′ . Trace the rays to find the position of the lens and of its focuses. What type of lens is it?

b. Solve the problem similar to the previous one using Figure.
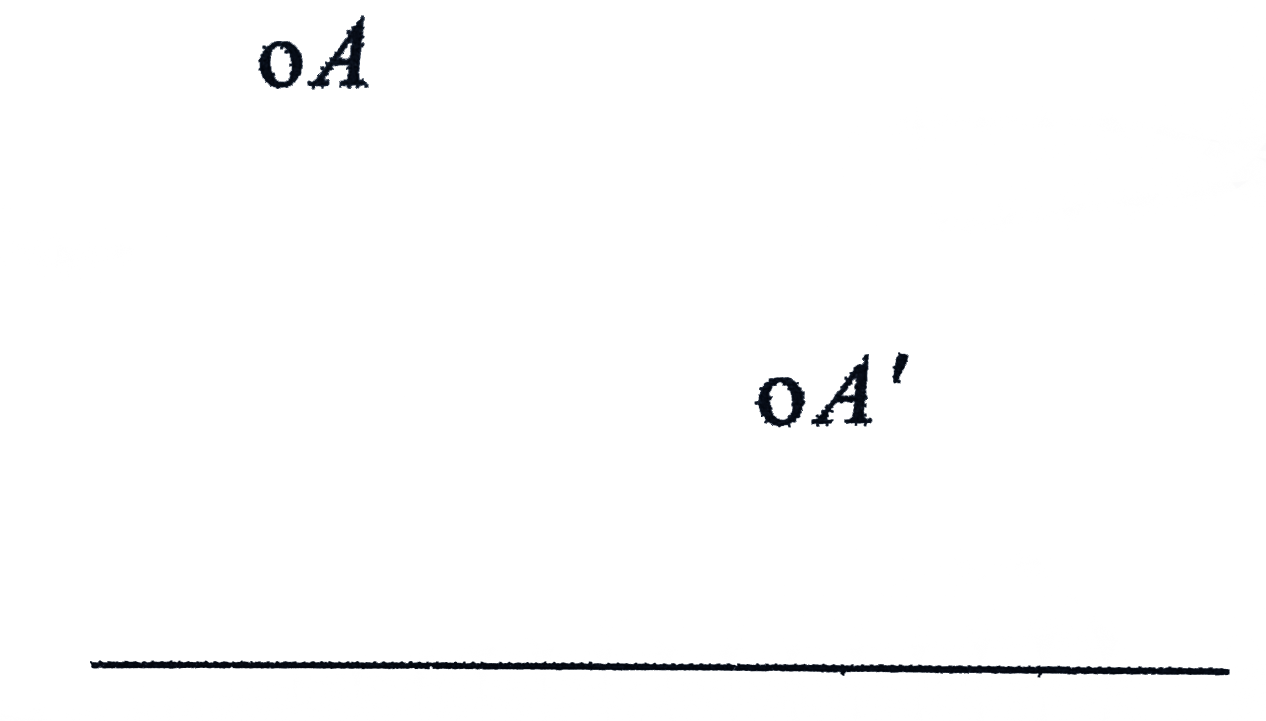
View SolutionMagnitude of focal length of a spherical mirror is f and magnitude of linear magnification is 12
View SolutionThe linear magnification of a convex mirror of focal length 15 cm is 1/3 . What is the distance of the object from the focus of the mirror ?
View SolutionAn obejct is placed at a distance 2f from the pole of a convex mirror of focal length f . The linear magnification is
View Solutionरेखीय आवर्धन से क्या तात्पर्य है ? गोलीय दर्पण के लिए रेखीय आवर्धन के सूत्र लिखिए।
View SolutionIn case of a spherical mirror show how magnification (m) depends on focal length (f) of the mirror and image distance (v).
View SolutionAn object is placed at a distance x from the principal focus of a spherical mirror of focal length f. The magnification of the image will be
View SolutionFor a spherical mirror if the linear magnification of the image be m what will be its lateral magnification ?
View SolutionAn object is placed at a distance x from the principal focus of a spherical mirror of focal length f. Calculate the magnification of the image.
View SolutionA short linear object of length L lies on the axis of a spherical mirror of focal length f at a distance K from the mirror. Calculate the axial length of the image.
View SolutionThe focal length of spherical mirror is
View Solution
