An optical system consists of a thin convex lens of focal length 30cm and a plane mirror placed 15cm behind the lens. An object is placed 15cm in front of the lens. The distance of the final image from the object is
60cm
30cm
75cm
45cm
The correct Answer is:B
To solve the problem step by step, we will follow these instructions:
Step 1: Identify the given data
- Focal length of the convex lens (F) = +30 cm (positive for convex lens)
- Distance of the plane mirror from the lens = 15 cm
- Object distance from the lens (U) = -15 cm (negative as per sign convention)
Step 2: Use the lens formula to find the position of the first image
The lens formula is given by:
1F=1V−1U
Substituting the known values:
130=1V1−1−15
This simplifies to:
130=1V1+115
To solve for V1, we first find a common denominator:
130=1V1+230
Rearranging gives:
1V1=130−230=−130
Thus, we find:
V1=−30 cm
This means the first image is formed 30 cm to the left of the lens.
Step 3: Determine the object distance for the mirror
The distance from the lens to the mirror is 15 cm. Since the first image is 30 cm to the left of the lens, the distance from the image to the mirror (acting as a new object for the mirror) is:
Distance from image to mirror=30 cm+15 cm=45 cm
Thus, the object distance for the mirror (U2) is:
U2=−45 cm
Step 4: Use the mirror formula to find the position of the second image
The mirror formula is similar to the lens formula:
1F=1V−1U
For a plane mirror, the focal length (F) is considered infinite, thus:
0=1V2−1−45
This simplifies to:
1V2=145
Thus, we find:
V2=+45 cm
This means the second image is formed 45 cm behind the mirror.
Step 5: Determine the object distance for the lens again
The second image (acting as an object for the lens) is now 45 cm behind the mirror. Since the mirror is 15 cm behind the lens, the total distance from the lens to the new object is:
Distance from lens to new object=15 cm+45 cm=60 cm
Thus, the object distance for the lens (U3) is:
U3=−60 cm
Step 6: Use the lens formula again to find the final image position
Using the lens formula again:
130=1V3−1−60
This simplifies to:
130=1V3+160
Finding a common denominator gives:
130=260+1V3
Rearranging gives:
1V3=130−260=130−130=0
Thus, we find:
V3=+60 cm
This means the final image is formed 60 cm to the right of the lens.
Step 7: Calculate the distance between the object and the final image
The object is located 15 cm in front of the lens, and the final image is located 60 cm behind the lens. Therefore, the distance between the object and the final image is:
Distance=60 cm−(−15 cm)=60+15=75 cm
Final Answer
The distance of the final image from the object is 75 cm.
- Focal length of the convex lens (F) = +30 cm (positive for convex lens)
- Distance of the plane mirror from the lens = 15 cm
- Object distance from the lens (U) = -15 cm (negative as per sign convention)
The lens formula is given by:
1F=1V−1U
Substituting the known values:
130=1V1−1−15
This simplifies to:
130=1V1+115
To solve for V1, we first find a common denominator:
130=1V1+230
Rearranging gives:
1V1=130−230=−130
Thus, we find:
V1=−30 cm
This means the first image is formed 30 cm to the left of the lens.
The distance from the lens to the mirror is 15 cm. Since the first image is 30 cm to the left of the lens, the distance from the image to the mirror (acting as a new object for the mirror) is:
Distance from image to mirror=30 cm+15 cm=45 cm
Thus, the object distance for the mirror (U2) is:
U2=−45 cm
The mirror formula is similar to the lens formula:
1F=1V−1U
For a plane mirror, the focal length (F) is considered infinite, thus:
0=1V2−1−45
This simplifies to:
1V2=145
Thus, we find:
V2=+45 cm
This means the second image is formed 45 cm behind the mirror.
The second image (acting as an object for the lens) is now 45 cm behind the mirror. Since the mirror is 15 cm behind the lens, the total distance from the lens to the new object is:
Distance from lens to new object=15 cm+45 cm=60 cm
Thus, the object distance for the lens (U3) is:
U3=−60 cm
Using the lens formula again:
130=1V3−1−60
This simplifies to:
130=1V3+160
Finding a common denominator gives:
130=260+1V3
Rearranging gives:
1V3=130−260=130−130=0
Thus, we find:
V3=+60 cm
This means the final image is formed 60 cm to the right of the lens.
The object is located 15 cm in front of the lens, and the final image is located 60 cm behind the lens. Therefore, the distance between the object and the final image is:
Distance=60 cm−(−15 cm)=60+15=75 cm
The distance of the final image from the object is 75 cm.
টপার এই প্রশ্নগুলো সমাধান করেছে
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions
1 Video
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Subjective
29 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Assertion And Reason
13 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
সম্পর্কিত প্রশ্ন
In Fig.(i), a lens of focal length 10cm is shown. It is cut into two parts and placed as shown in Fig.(ii). An object AB of light 1cm is placed at a distance of 7.5cm. The height of the image will be

View SolutionThe laws of reflection or refraction are the same for sound as for light. The index of refraction of a medium (for sound) is defind as the ratio of the speed of sound in air 343m/s to the speed of sound in the medium.
What is the index of refraction (for sound) of water (v=1498m/s)?
What is the critical angle θ, for total reflection of sound from water?
View SolutionAssertion: Therefore is a glass slab between Ram and Anoop. Then, Ram appears nearer to Anoop as compared to the actual distance between them.
Reason: Ray of light starting from Ram will undergo two times refraction before reaching Anoop.
View SolutionA point source of light S is placed at a distance 10 cm in front of the centre of a mirror of width 20 cm suspended vertically on a wall. An insect walks with a speed 10cm/s in front of the mirror along a line parallel to the mirror at a distance 20 cm from it as shown in figure. find the maximum time during which the insect can see the image of the source S in the mirror.
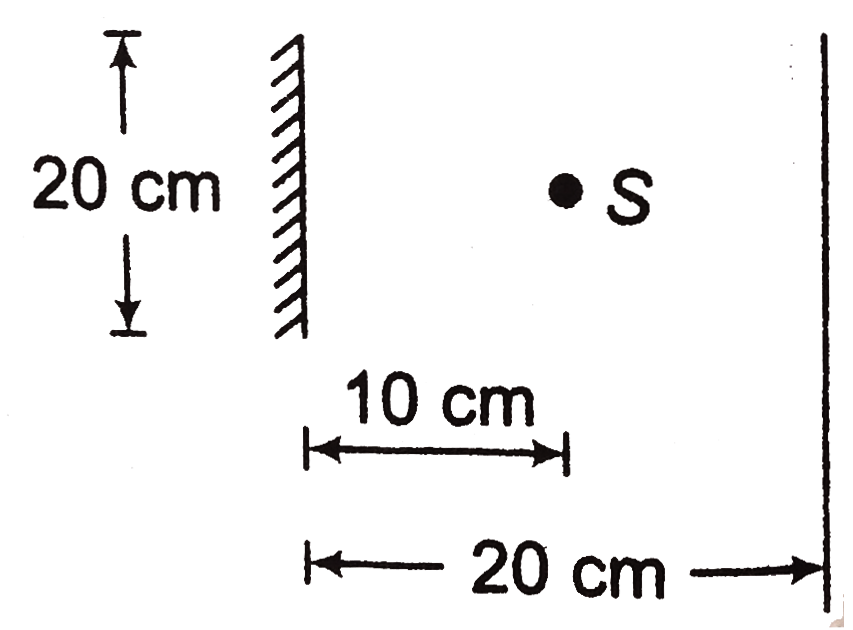
View SolutionCan the potential barrier across a p-n junction be measured by simply connecting a voltmeter across the junction ?
View SolutionA biconvex lens of focal length 15 cm is in front of a plane mirror. The distance between the lens and the mirror is 10 cm. A small object is kept at a distance of 30 cm from the lens. The final image is
View SolutionAn optical system consists of a thin convex lens of focal length 30 cm and a plane mirror placed 15 cm behind the lens. An object is placed 15 cm in front of the lens. The distance of the final image from the object is
View SolutionA thin convex lens of focal length 30cm is placed in front of a plane mirror. An object is placed at a distance x from the lens (not in between lens and mirror ) so that its final image coincides with itself. Then, the value of x is
View SolutionA point object is placed 60 cm in front of a convex lens of focal length 15 cm . A plane mirror is placed 10 cm behind the convex lens. Where is the image formed by the system ?
View SolutionA convex lens of focal length 15 cm is placed on a plane mirror. An object is placed 20 cm from the lens. The image is formed
View SolutionA convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
View Solution15 सेमी फोकस-दूरी वाला एक द्वि-उत्तल लेन्स समतल दर्पण के सामने रखा है | लेन्स तथा दर्पण की बीच दूरी 10 सेमी है | लेन्स से 30 सेमी की दूरी पर एक छोटी वस्तु रखी गयी है | इसका अंतिम प्रतिबिम्ब :
View SolutionAn object is placed at a distance of 15 cm from a convex lens. If the focal length of the lens is 60 cm, find the image distance.
View SolutionA biconvex lens of focal length 15 cm is in front of a plane mirror. The distance between the lens and the mirror is 10 cm. A small object is kept at a distance of 30 cm from the lens. The final image is
View SolutionA biconvex lens of focal length 15 cm is in front of a plane mirror. The distance between the lens and the mirror is 10 cm. A small object is kept at a distance of 30 cm from the lens. The final image is
View Solution

