A taut string for which mass per unit length μ=5.0×10−2kg/m is under tension of 80N. How much power in watt upto one decimal points must be supplied to the string to generate siusodial be supplied to the string to generate sinusoidal wave at a frequency of 6.0Hz and amplitude of 6.00cm
5.2W
10.4W
2.6W
7.8W
The correct Answer is:A
To find the power that must be supplied to the string to generate a sinusoidal wave, we can use the formula for power in a wave on a string:
P=2πf2μA2v
where:
- P is the power,
- f is the frequency,
- μ is the mass per unit length,
- A is the amplitude,
- v is the velocity of the wave on the string.
Step 1: Calculate the velocity of the wave on the string
The velocity v of a wave on a string under tension T is given by:
v=√Tμ
Given:
- T=80N
- μ=5.0×10−2kg/m
Substituting the values:
v=√805.0×10−2
v=√1600
v=40m/s
Step 2: Convert amplitude to meters
The amplitude A is given in centimeters, so we need to convert it to meters:
A=6.00cm=6.00×10−2m
Step 3: Substitute values into the power formula
Now we can substitute the values into the power formula:
P=2πf2μA2v
Given:
- f=6.0Hz
- μ=5.0×10−2kg/m
- A=6.00×10−2m
- v=40m/s
Substituting these values:
P=2π(6.0)2(5.0×10−2)(6.00×10−2)2(40)
Calculating each part step by step:
1. Calculate (6.0)2:
(6.0)2=36
2. Calculate (6.00×10−2)2:
(6.00×10−2)2=36×10−4
3. Now substitute back into the equation:
P=2π(36)(5.0×10−2)(36×10−4)(40)
4. Combine the constants:
P=2π×36×5.0×36×40×10−6
5. Calculate the numerical value:
P=2π×36×5.0×36×40
P=2π×7200
P≈45238.934
6. Finally, multiply by 10−6:
P≈0.0452W
7. Rounding to one decimal point:
P≈5.2W
Final Answer:
The power that must be supplied to the string is approximately 5.2 W.
- P is the power,
- f is the frequency,
- μ is the mass per unit length,
- A is the amplitude,
- v is the velocity of the wave on the string.
The velocity v of a wave on a string under tension T is given by:
- T=80N
- μ=5.0×10−2kg/m
v=√1600
v=40m/s
The amplitude A is given in centimeters, so we need to convert it to meters:
Now we can substitute the values into the power formula:
- f=6.0Hz
- μ=5.0×10−2kg/m
- A=6.00×10−2m
- v=40m/s
(6.0)2=36
(6.00×10−2)2=36×10−4
P=2π(36)(5.0×10−2)(36×10−4)(40)
P=2π×36×5.0×36×40×10−6
P=2π×36×5.0×36×40
P=2π×7200
P≈45238.934
P≈0.0452W
P≈5.2W
The power that must be supplied to the string is approximately 5.2 W.
Topper's Solved these Questions
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:ONLY ONE OPTION IS CORRECT
Explore 62 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:More Than One Option is Correct
Explore 23 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Subjective Questions
Explore 2 Videos
- VECTORSBook:DC PANDEY ENGLISHChapter:VECTORSExercise:Medical enrances gallery
Explore 9 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
Similar Questions
The frequency of sonometer wire is f. The frequency becomes f/2 when the mass producing the tension is completely immersed in water and on immersing the mass in a certain liquid, frequency becomes f/3. The relative density of the liquid is
View SolutionA stationary observer receiver a sound of frequency f0=2000Hz .Sourece is moving with constant velocity on a road at some non-zero prependicular distance from observer . The apparent frequncy f varies with times as show in figure . Speed of sound =300m/s. Find the maximum apparent frequency.
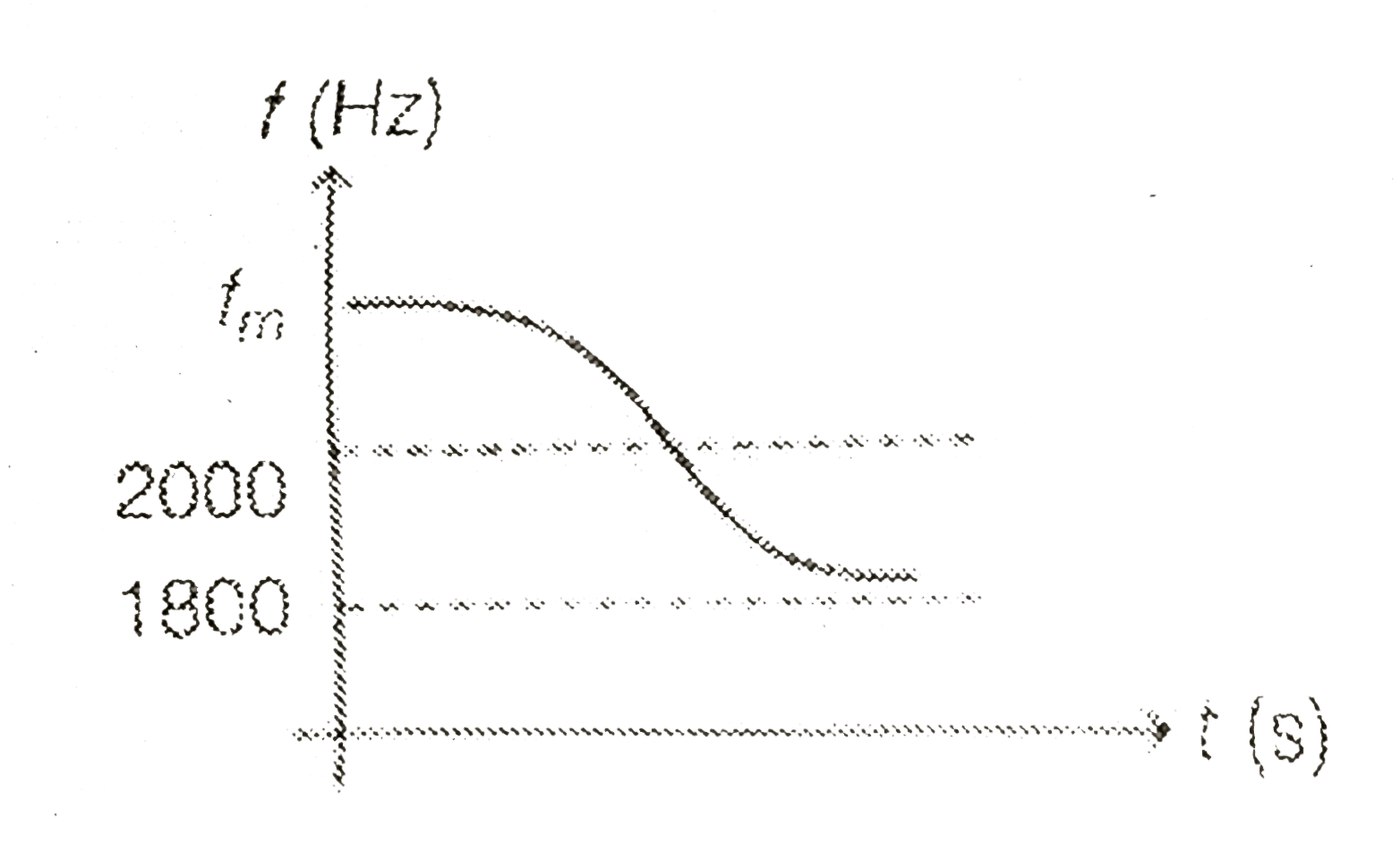
View SolutionTwo long strings A and B, each having linear mass density 1.2×10−2kgm−1, are stretched by different tensions 4.8 N and 7.5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A ?
View SolutionIf the magnitude of sum of two vectors is equal to the magnitude of difference of the two vector, the angle between these Vector is
View SolutionThe figure shows the variation of potential energy of a particle as a function pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
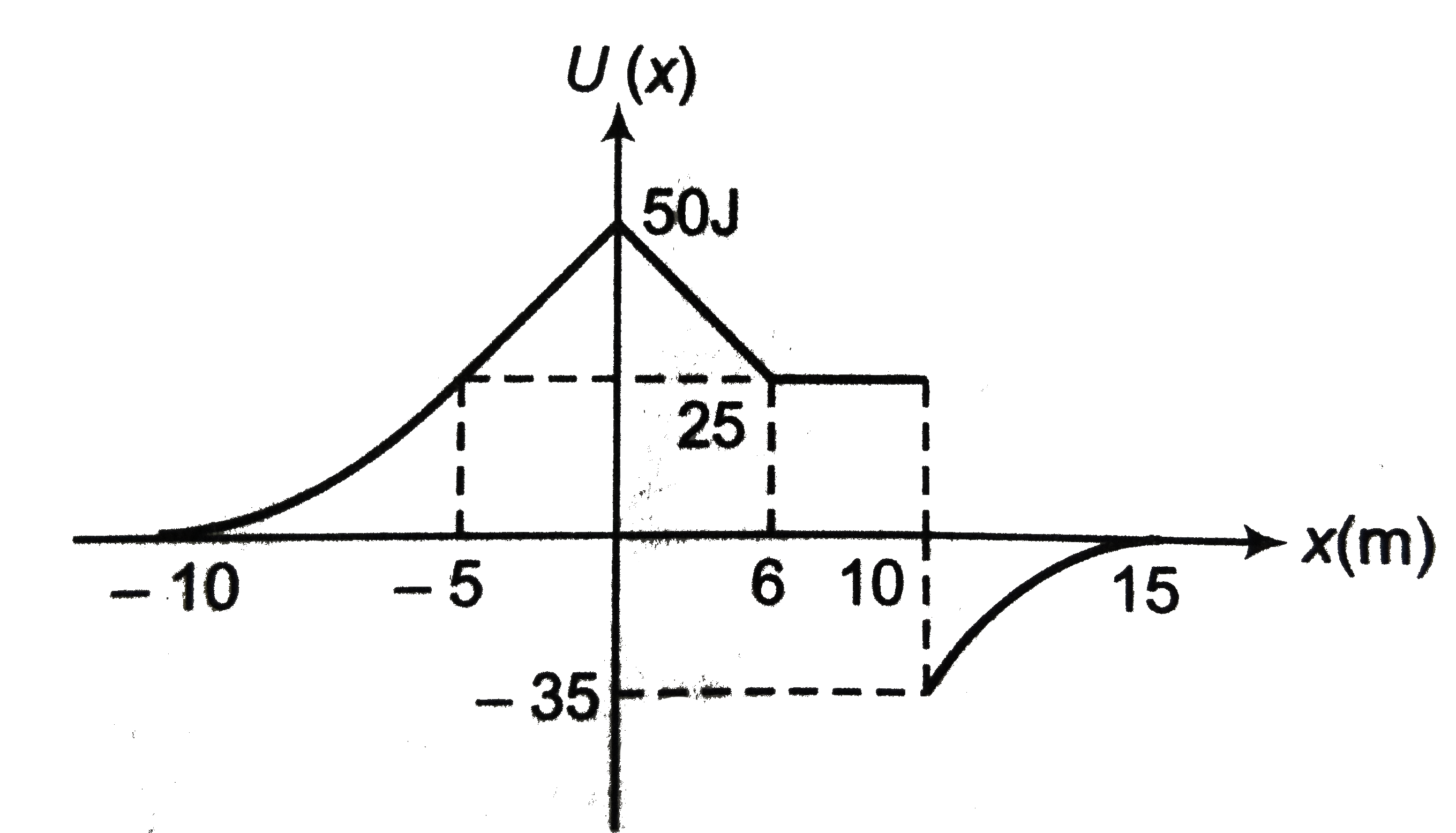
If total mechanical energy of the particle is 25J, then it can found in the region
View SolutionThe frequency (f) of a stretched string depends upen the tension F (dimensions of form ) of the string and the mass per unit length mu of string .Derive the formula for frequency
View SolutionA taut string for which mu = 5.00 xx 10^(-2) kg//m under a tension of 80.0N . How much power must be supplied to the string to generate sinusoidal waves at a frequency of 60.0 Hz and an amplitude of 6.00 cm ?
View SolutionPower supplied to a vibrating string: A string with linear mass density μ=5.00×10−2kg/m is under a tension of 80.0 N. how much power must be supplied to the string to generate sinusoidal waves at a frequency of 60.0 HZ and an amplitude of 6.00 cm?
View SolutionA taut string for which mass per unit length mu=5.0xx10^(-2)kg//m is under tension of 80N. How much power in watt upto one decimal points mus be supplied to the string to generate siusodial be supplied to the string to generate sinusoidal wave at a frequency of 6.0Hz and amplitude of 6.00cm
View SolutionA string of mass 0.250 kg is under a tension of 2 N. The length of the stretched string is 2 m. A transverse wave disturbance starts at one end of the string . How long will the disturbance take to reach the other end ?
View SolutionString-1 is connected with string-2 The mass per unit length in string-1 is μ1 and mass per unit length in string-2 is 4μ1. The tension in the strings is T .A travelling wave is coming from the left .What fraction of the energy in the incident wave goes into string-2?
View SolutionA string of total mass 100g & total length 2m is under tension due to the weight of an object of mass 8kg .If the resulting sinusoidal wave in the string has an amplitude of 6cm and frequency 60Hz the power that must be supplied to the string is
View SolutionThe frequency ( nu ) of transverse wave on a string may depend upon (i) length L of string (ii) tension T in the string and (iii) mass per unit length m of the string Derive the formula for frequency with the help of dimensions.
View SolutionA taut string from which mu= 5.0 xx 10^(-2) kg/m is under tension of 80 N. How much power in watt upto one decimal point must be supplied to the string to generated sinusoidal waves at a frequency of 6.0 Hz and amplitude of 6.00 cm .
View SolutionConsider a harmonic wave travelling on a string of mass per unit length μ The wave has a velocity v, amplitude A and frequency f. The power transmitted by a harmonic wave on the string is proportional to (take constant of proportionality as 2π2)
View Solution
