An air column in a pipe, when is closed at one end, is in resonance with a vibrating tuning fork of frequency 264HZ. If υ=330m/s, the length of the column in cm is (are)
31.25
62.5
93.75
125
The correct Answer is:A, C
To find the length of the air column in a pipe closed at one end that is in resonance with a vibrating tuning fork, we can use the formula for the fundamental frequency of a closed organ pipe.
1. Identify the Given Values:
- Frequency (f) = 264 Hz
- Speed of sound in air (v) = 330 m/s
2. Use the Formula for the Fundamental Frequency:
The fundamental frequency (f) of a closed organ pipe is given by the formula:
f=v4L
where L is the length of the air column.
3. Rearranging the Formula:
To find the length L, we can rearrange the formula:
L=v4f
4. Substituting the Values:
Now substitute the values of v and f into the equation:
L=330m/s4×264Hz
5. Calculating the Length:
Calculate the denominator:
4×264=1056
Now, calculate L:
L=3301056≈0.3125m
6. Convert to Centimeters:
To convert the length from meters to centimeters, multiply by 100:
L=0.3125×100=31.25cm
7. Conclusion:
The length of the air column in the pipe is 31.25cm.
Additional Options:
- To find other possible lengths for higher harmonics, we can use the odd harmonics (n = 1, 3, 5, ...):
- For n = 3:
L=v4×3f=3304×792≈0.09375m=93.75cm
- For n = 5, similar calculations can be done.
Final Answer:
The correct options for the length of the column are:
- 31.25cm (for n = 1)
- 93.75cm (for n = 3)
- Frequency (f) = 264 Hz
- Speed of sound in air (v) = 330 m/s
The fundamental frequency (f) of a closed organ pipe is given by the formula:
f=v4L
where L is the length of the air column.
To find the length L, we can rearrange the formula:
L=v4f
Now substitute the values of v and f into the equation:
L=330m/s4×264Hz
Calculate the denominator:
4×264=1056
Now, calculate L:
L=3301056≈0.3125m
To convert the length from meters to centimeters, multiply by 100:
L=0.3125×100=31.25cm
The length of the air column in the pipe is 31.25cm.
- To find other possible lengths for higher harmonics, we can use the odd harmonics (n = 1, 3, 5, ...):
- For n = 3:
L=v4×3f=3304×792≈0.09375m=93.75cm
- For n = 5, similar calculations can be done.
The correct options for the length of the column are:
- 31.25cm (for n = 1)
- 93.75cm (for n = 3)
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions
20 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Matrix Matching
16 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - ONLY ONE OPTION IS CORRECT
62 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
[Q.Nos. 1-2] y(x, t) equation of a lingiutudinal wave is given as
y=10−22(π)[1000t+5017x] (All Si units
At t = 0 Change in pressure is maximum at x=……….m.
View SolutionA sound source has frequency f. Source and observer both have same speed.For the apparent frequency observed by observer match the following.

View SolutionThe frequency of sonometer wire is f. The frequency becomes f/2 when the mass producing the tension is completely immersed in water and on immersing the mass in a certain liquid, frequency becomes f/3. The relative density of the liquid is
View SolutionIf the magnitude of sum of two vectors is equal to the magnitude of difference of the two vector, the angle between these Vector is
View SolutionThe figure shows the variation of potential energy of a particle as a function pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
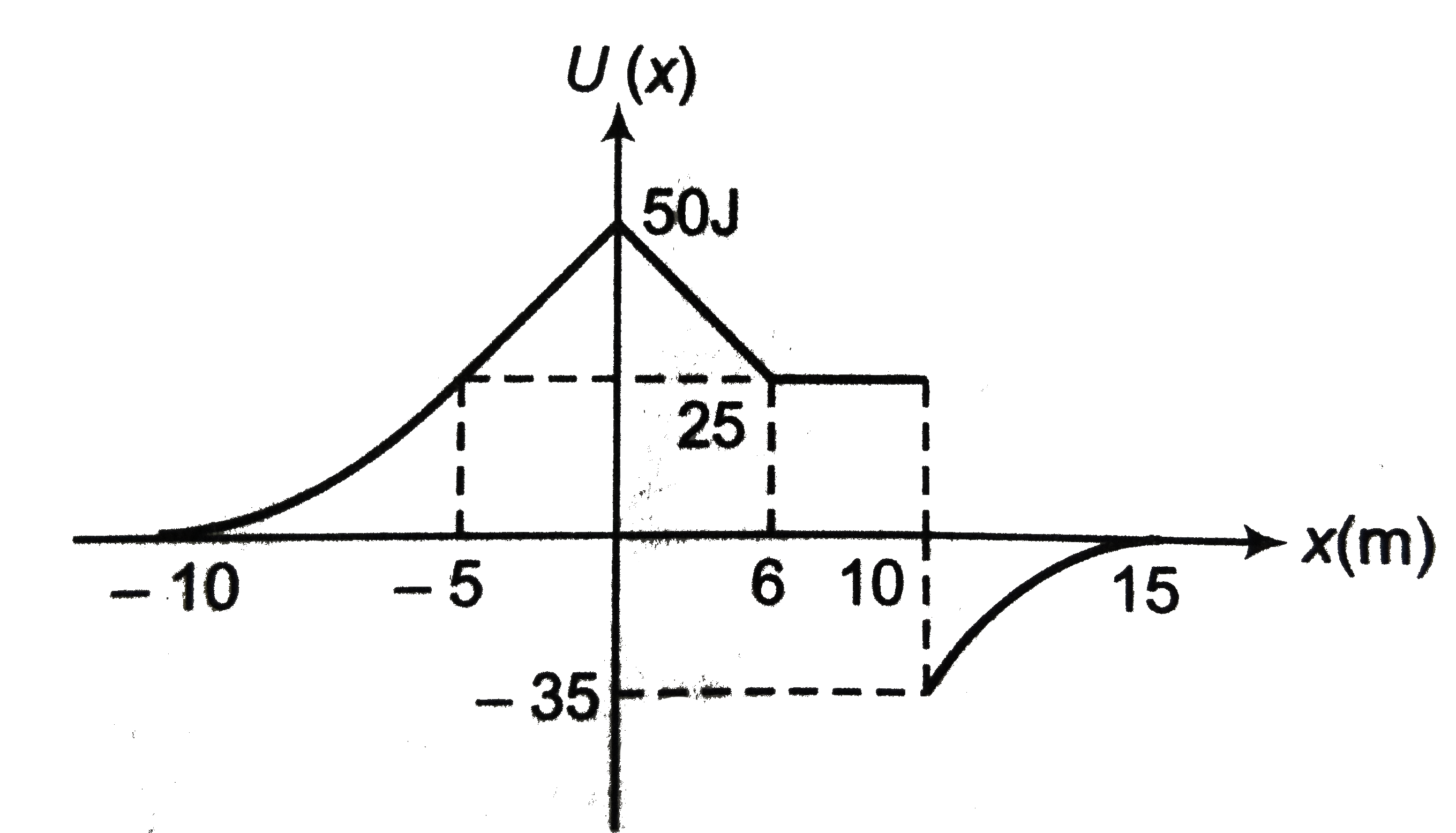
If total mechanical energy of the particle is 25J, then it can found in the region
View SolutionAn air columbn in pipe, which is closed at one end, will be in resonance with a vibrating tuning fork of frequency 264 Hz if the length of the column in cm is :
View SolutionAn air column in a pipe, when is closed at one end, is in resonance with a vibrating tuning fork of frequency 264HZ. If υ=330m/s, the length of the column in cm is (are)
View SolutionAn air column in a pipe which is closed at one end will be in resonance with a vibrating tuning fork of frequency 264 Hz if the length of the air column in cm is (Speed of sound in air = 340 m/s)
View SolutionThe air column in a pipe closed at one end is made to vibrate in its second overtone by a tuning fork of frequency 440 Hz. The speed of sound in air is 330 m/s. find the length of air column.
View SolutionAn air column in a pipe of length 1 m and closed at one end, will be in resonace with a vibrating tuning fork of frequency 250 Hz, if the length of the column is [v = 330 m/s]
View SolutionAn air column in a pipe, which is closed at one end will be in resonace with a vibrating tuning fork of frequency 264 Hz for various lengths. Which one of the following lengths is not possible ? [v = 330 m/s]
View SolutionAn air column in a pipe, which is closed at one end will be in resonance with a vibrating tunning fork of frequency 264 Hz, If the length of column is :-
View SolutionAn air column in a pipe which is closed at one end will be in resonance with a vibrating tuning fork of frequency 264 Hz if the length of the air column in cm is (Speed of sound in air = 340 m/s)
View Solutionएक बन्द ऑर्गन पाइप 264 हार्ट्ज आवृत्ति के कम्पित स्वरित्र , द्विभुज के साथ अनुनाद में होगा यदि स्तम्भ की लम्बाई है (वायु में ध्वनि की चाल =330 मी/से )
View SolutionThe air column in a pipe which is closed at one end will be in resonance with a vibrating tuning fork at a frequency 250 Hz. If the length of the air column is :
View Solution

