A car is negotiating a curved road of radius R. The road is banked at angle θ. The coefficeint of friction between the tyres of the car and the road is μs. The maximum safe velocity on this road is
4.5m/w
5.0 m/s
5.7 m/s
6.2m/s
The correct Answer is:C
To find the maximum safe velocity of a car negotiating a banked curve, we can follow these steps:
1. Understanding the Forces Acting on the Car:
- When a car is negotiating a banked curve, the forces acting on it include gravitational force (mg), normal force (N), and frictional force (f).
- The gravitational force acts vertically downward, while the normal force acts perpendicular to the surface of the road.
2. Setting Up the Equations:
- The car moves in a circular path, so we can analyze the forces in both horizontal and vertical directions.
- In the horizontal direction, the net force provides the centripetal force required for circular motion:
Nsinθ+fcosθ=mv2R
- In the vertical direction, the forces must balance:
Ncosθ=mg+fsinθ
3. Expressing Frictional Force:
- The frictional force can be expressed in terms of the coefficient of static friction (μs):
f=μsN
- Substituting this into the horizontal force equation gives:
Nsinθ+μsNcosθ=mv2R
4. Substituting for Normal Force:
- From the vertical force balance, we can express N:
N=mg+μsNsinθcosθ
- Rearranging gives:
Ncosθ=mg+μsNsinθ
5. Combining the Equations:
- We can substitute the expression for N from the vertical balance into the horizontal balance:
(mg+μsNsinθ)sinθcosθ+μs(mg+μsNsinθ)cosθcosθ=mv2R
6. Solving for Maximum Velocity:
- After simplifying and rearranging the equations, we arrive at:
v2max=Rg(tanθ+μs)÷(1−μstanθ)
- Taking the square root gives:
vmax=√Rg(tanθ+μs)÷(1−μstanθ)
Final Result:
The maximum safe velocity vmax is given by:
vmax=√Rg(tanθ+μs)÷(1−μstanθ)
- When a car is negotiating a banked curve, the forces acting on it include gravitational force (mg), normal force (N), and frictional force (f).
- The gravitational force acts vertically downward, while the normal force acts perpendicular to the surface of the road.
- The car moves in a circular path, so we can analyze the forces in both horizontal and vertical directions.
- In the horizontal direction, the net force provides the centripetal force required for circular motion:
Nsinθ+fcosθ=mv2R
- In the vertical direction, the forces must balance:
Ncosθ=mg+fsinθ
- The frictional force can be expressed in terms of the coefficient of static friction (μs):
f=μsN
- Substituting this into the horizontal force equation gives:
Nsinθ+μsNcosθ=mv2R
- From the vertical force balance, we can express N:
N=mg+μsNsinθcosθ
- Rearranging gives:
Ncosθ=mg+μsNsinθ
- We can substitute the expression for N from the vertical balance into the horizontal balance:
(mg+μsNsinθ)sinθcosθ+μs(mg+μsNsinθ)cosθcosθ=mv2R
- After simplifying and rearranging the equations, we arrive at:
v2max=Rg(tanθ+μs)÷(1−μstanθ)
- Taking the square root gives:
vmax=√Rg(tanθ+μs)÷(1−μstanθ)
The maximum safe velocity vmax is given by:
vmax=√Rg(tanθ+μs)÷(1−μstanθ)
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Match the columns
Explore 3 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
Three balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O.find the tensions .
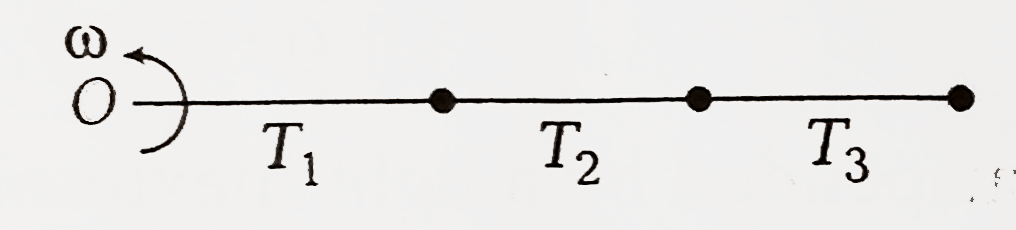
View SolutionA ladder AP of length 5m inclined to a vertical wall is slipping over a horizontal surface with velocity of 2m/s, when A is at distance 3m from ground. What is the velocity of COM at this moment?

View SolutionMajor parts of communications systems are:
View SolutionA car is negotisting a curved road of radius R . The road is banked at an angle theta. The coefficient of friction between the tyres of the car and the road is mu_(s) . The maximum safe velocity on this road is:
View SolutionA car is negotiating a curved road of radius R. The road is banked at angle θ. The coefficeint of friction between the tyres of the car and the road is μs. The maximum safe velocity on this road is
View Solutionएक कार R त्रिज्या की वकृत ( curved ) सड़क पर गतिमान है। वह सड़क θ कोण पर झुकी है । कार के टायरों व् सड़क के बिच घर्षण गुणांक μs है । इस सड़क पर कार का अधिकतम सुरक्षा वेग है :
View SolutionA car is negotiating a curved road of radius R. The road is banked at an angle theta . The coefficient of friction between the types of the car and the road is mu_s . The maximum safe velocity on this road is
View SolutionA car is negotiating a curved road of radius R. The road is banked at an angle theta . The coefficient of friction between the types of the car and the road is mu_(s) . The maximum safe velocity on this road is
View SolutionA car is negotiating a curved road of radius R. The road is banked at an angle. The coefficient of friction between the types of the car and the road is μs. The maximum safe velocity on this road is
View SolutionA car is negotiating a curved road of radius R. The road is banked at an angle θ. The coefficient of friction between the tyres of the car and the road is μs. The maximum safe velocity on this road is
View SolutionA car is negotiating a curved road of radius R. The road is banked at an angle theta . The coefficient of friction between the types of the car and the road is mu_(s) . The maximum safe velocity on this road is
View SolutionA car is negotiating a curved road of radius R. The road is banked at an angle theta . The coefficient of friction between the types of the car and the road is mu_(s) . The maximum safe velocity on this road is
View SolutionA car is negotiating a curved road of radius R. The road is banked at angle theta . The coefficeint of friction between the tyres of the car and the road is mu_(s) . The maximum safe velocity on this road is
View Solutionएक कार त्रिज्या R की एक वक्रीय सड़क पर चल रही है। सड़क के बंकन का कोण θ है । कार के पहियों और सड़क के बीच घर्षण गुणांक μS है। इस सड़क पर अधिकतम सुरक्षित वेग है :
View SolutionA car is negotiating a curved road of radius R. banked at an angle theta . The coefficient of frictie the tyres of the car and the road is mu_(s) . The man velocity on this road is:
View Solution
