The magnetic flux density applied in a cyclotron is 3⋅5T. What will be the frequency of electric field that must be applied between the dees in order (a) to accelerate protons (b) α-particles? mass of proton 1⋅67×10−27kg.
To solve the problem, we need to find the frequency of the electric field that must be applied between the dees of a cyclotron to accelerate protons and alpha particles. We will use the following formulas related to magnetic fields and circular motion.
1. Understanding the Cyclotron:
- A cyclotron accelerates charged particles using a magnetic field and an alternating electric field. The magnetic field causes the particles to move in circular paths, while the electric field accelerates them.
2. Given Data:
- Magnetic flux density, B=3.5T
- Mass of proton, mp=1.67×10−27kg
- Charge of proton, qp=1.6×10−19C
- Mass of alpha particle, mα=4×mp
- Charge of alpha particle, qα=2×qp
3. Finding the Frequency for Protons:
- The centripetal force required for circular motion is provided by the magnetic force:
qpvB=mpv2r
- Rearranging gives us:
r=mpvqpB
- The time period T for one complete revolution is given by:
T=2πrv
- Substituting for r:
T=2π(mpvqpB)v=2πmpqpB
- The frequency f is the reciprocal of the time period:
f=1T=qpB2πmp
4. Substituting Values for Protons:
fp=(1.6×10−19C)(3.5T)2π(1.67×10−27kg)
- Calculating:
fp=5.6×10−192×3.14×1.67×10−27≈5.35×107Hz
5. Finding the Frequency for Alpha Particles:
- Using the same formula for frequency, but substituting the mass and charge of the alpha particle:
fα=qαB2πmα=(2×1.6×10−19C)(3.5T)2π(4×1.67×10−27kg)
- Calculating:
fα=11.2×10−192×3.14×6.68×10−27≈2.67×107Hz
Final Answers:
- (a) Frequency for protons: fp≈5.35×107Hz
- (b) Frequency for alpha particles: fα≈2.67×107Hz
- A cyclotron accelerates charged particles using a magnetic field and an alternating electric field. The magnetic field causes the particles to move in circular paths, while the electric field accelerates them.
- Magnetic flux density, B=3.5T
- Mass of proton, mp=1.67×10−27kg
- Charge of proton, qp=1.6×10−19C
- Mass of alpha particle, mα=4×mp
- Charge of alpha particle, qα=2×qp
- The centripetal force required for circular motion is provided by the magnetic force:
qpvB=mpv2r
- Rearranging gives us:
r=mpvqpB
- The time period T for one complete revolution is given by:
T=2πrv
- Substituting for r:
T=2π(mpvqpB)v=2πmpqpB
- The frequency f is the reciprocal of the time period:
f=1T=qpB2πmp
fp=(1.6×10−19C)(3.5T)2π(1.67×10−27kg)
- Calculating:
fp=5.6×10−192×3.14×1.67×10−27≈5.35×107Hz
- Using the same formula for frequency, but substituting the mass and charge of the alpha particle:
fα=qαB2πmα=(2×1.6×10−19C)(3.5T)2π(4×1.67×10−27kg)
- Calculating:
fα=11.2×10−192×3.14×6.68×10−27≈2.67×107Hz
- (a) Frequency for protons: fp≈5.35×107Hz
- (b) Frequency for alpha particles: fα≈2.67×107Hz
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Check point
Explore 54 Videos
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Taking it together
Explore 75 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Level 2 Subjective
Explore 5 Videos
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:MCQ_TYPE
Explore 1 Video
Similar Questions
The magnetic field applied in a cyclotron is 3.5 T. What will be the frequency of electric field that must be applied between the does in order to accelerate protons ?
View SolutionMagnetic field applied on a cyclotron is 0⋅7T and radius of its dees is 1⋅8m. What will be the energy of the emergent protons in MeV? Mass of proton=1⋅67×10−27kg.
View SolutionMagnetic field applied on a cyclotron is 0⋅7T and radius of its dees is 1⋅8m. What will be the energy of the emergent protons in MeV? Mass of proton=1⋅67×10−27kg.
View SolutionFind (a) the total number and (b) the total mass of protons in 34 mg of NH3 at S.T.P. (Assume the mass of proton =1.6726×10−27kg)
View Solution(a) Draw a schematic sketch of a cyclotron. Explain clearly the role of crossed electric and magnetic field in accelerating the charge. Hence derive the expression for the kinetic energy acquired by the particles.
(b) An α-particle and a proton are relased form the centre of the cyclotron and made to accelerate.
(i) Can both be accelerated at the same cyclotron frequency? Give reason to justify your answer.
(ii) When they are accelerated in turn, which of the two will have higher velocity at the exit slit of the dees ?
View SolutionIf the cyclotron oscillator frequency is 16 MHz, then what should be the operating magnetic field for accelerating the proton of mass 1.67×10−27kg?
View SolutionAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.
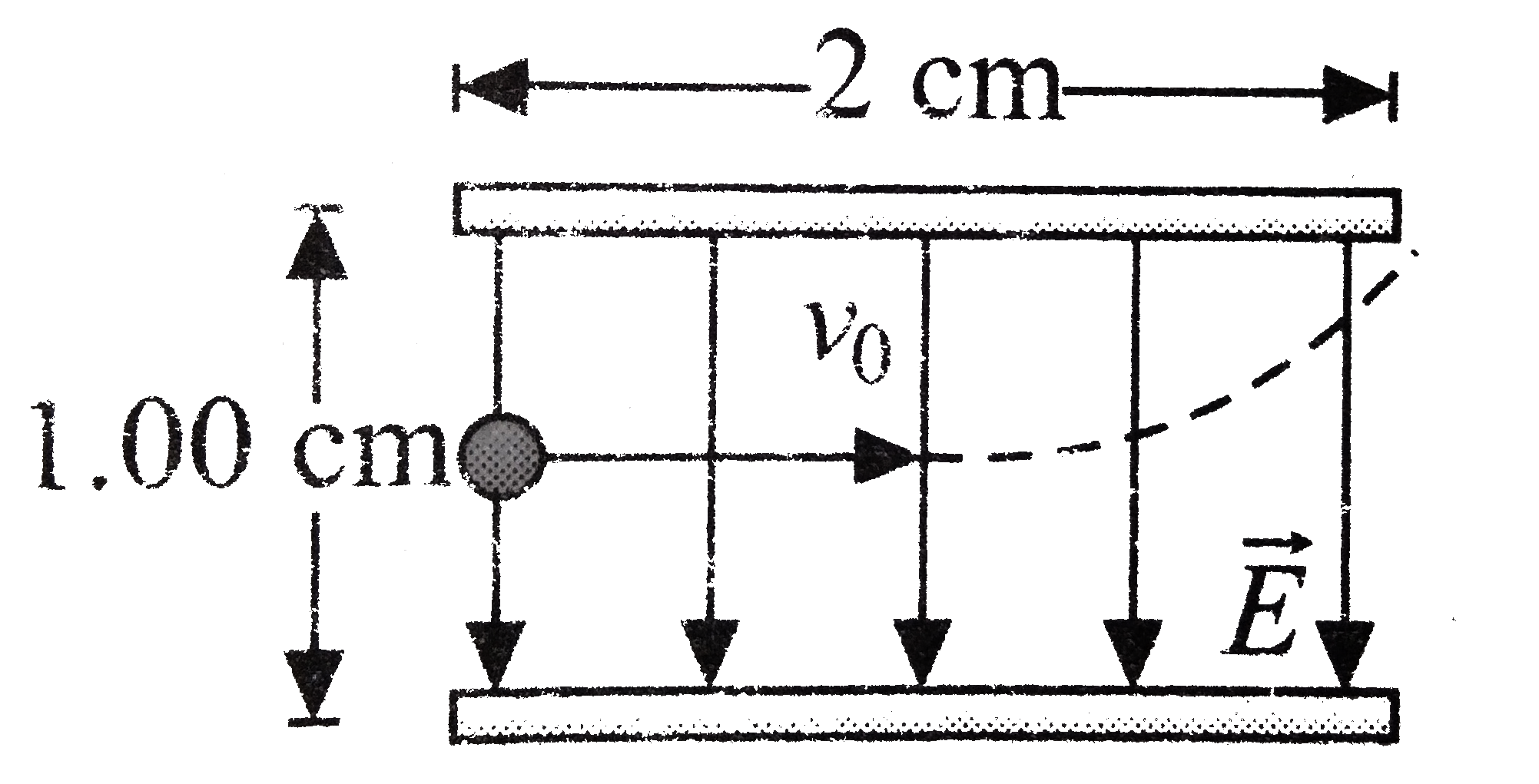
The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).
View SolutionAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.

The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).
View SolutionA proton projected in a magnetic field of 0.020 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton=1.6X10−27kg.
View SolutionA cyclotron is device for accelerating ions and charged particles. It was developed by Lawerence in 1932.
The heart of the appritus consists of a split metal pillbox. Figure sHOws top and front views of the halves called dees. A rapidly oscilating potential difference is applied between the Dees. This produces an oscilating electric field in the gap between the dees, the region inside each dee being essentially free of electric field. The Dees are enclosed in an evaccutaed container, and the entire unit is placed in a uniform magnetic field B whose direction is normal to the plane Of Dees, A charged particle of mass 'm' and charge 'q' in the gap between the dees, it moves with constant speed in a semi-circle.
The period of uniform circular motion is T=2πmqB and is independant of speed. If the time-period of the oscilating elctric field is equal to this time, then the charged particle will be accelerated again and again

Answer the following questions (consider the mass of particles remains constant during motion):
A cyclotron has been adjusted to accelereted deutrons. It is now to be adjusted to accelerate other particles , for this following changes may be made:
(a) In order to keep the frequency of oscillating electric field same, the magnetic field is halved for proton
(b) If the magnetic field remain unchanged, the oscillation frequency of electric field should be halved for α particle
(c ) If the magnetic field remain unchanged, the oscillation frequency of electric field should be double for proton
(d) If the frequency of oscillating electric field is kept same, the magnetic field should be kept same for α particle
View Solution
