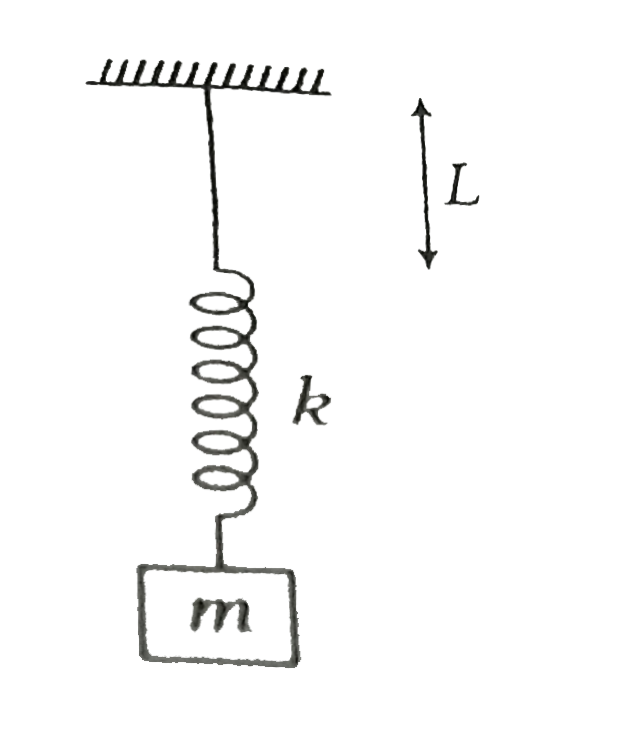
One end of a long metallic wire of length L is tied to the ceiling. The other end is tied to massless spring of spring constant k. A mass m hangs freely from the free end of the spring . The area of cross-section and Young's modulus of the wire are A and Y respectively . If the mass is slighty pulled down and released , it will oscillate with a time period T equal to
2π√mk
2π√m(YA+kL)YAK
2π√mYAkL
2π√mLYA
The correct Answer is:B
(b) Wire is equivalent to a spring of spring constant, k'=AYL
k' and k are in series
keq=k'kk'+k=(AY/L)+k(AYL)+k=AYkAY+kL
T=2π√mkeq=2π√m(AY+kL)AYk
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Match the columns
4 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.3
15 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
Match the following
∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣ Table-1 Table-2(A) Steel(P) Young's modulus of elasticity(B) Water(Q) Bulk modulus of elasticity(C) Hydrogen gas filled(R) sheer modulus of in a chamber elasticity∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionThe length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. Then natural length of the wire is
View SolutionIf the volume of a wire remains constant when subjected to tensile stress, the value of Poisson's ratio of the material of the wire is
View SolutionThe current density in a wire is 10A/cm2 and the electric field in the wire is 5 V/cm. If p = resistivity of material, σ= conductivity of the material then (in SI unit)
View SolutionThe centres of two identical small conducting sphere are 1 m apart. They carry charge of opposite kind and attract each other with a force F. when they connected by conducting thin wire they repel each other with a force F/3. The ratio of magnitude of charges carried by the spheres initially in n:1. Find value of n
View SolutionOne end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
View SolutionA metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
View SolutionOne end of a long mettalic wire of length L is tied to the ceiling. The other end is tied to massless spring of spring constant K. A mass M hangs freely from the free end of the spring. The area of cross-section and Young's modulus of the wire are A and Y respectively. If the mass is slightly pulled down and released, it will oscillate with a time period T equal to
View SolutionL लम्बाई के लम्बे धात्विक तार का एक सिरा छत से बंधा है। इसका दूसरा सिरा एक द्रव्यमानहीन स्प्रिंग से बंधा है जिसका बल नियतांक k है। स्प्रिंग के मुक्त सिरे से एक द्रव्यमान m स्वतंत्रतापूर्वक लटका है। तार के परिच्छेद का क्षेत्रफल तथा यंग गुणांक क्रमशः A तथा Y है। यदि द्रव्यमान को थोड़ा नीचे खींचकर छोड़ दे, तो इसके दोलनों का आवर्तकाल होगा।
View SolutionA spring of spring constant 'k' is supported from one end and tied by a mass 'm' at the other end. Write the formula to find the period of oscillation of the mass body. (Ignore the mass of the spring).
View SolutionOne end of a long metallic wire of length L, area of cross-section A and Young's modulus Y is tied to the ceiling. The other end is tied to a massless spring of force constant k and a mass m is hung from the free end of the spring. If m is slightly pulled down and released, then its time period of oscillation is
View SolutionA metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
View SolutionOne end of a long metallic wire of length L is tied to the ceiling. The other end is tied to a spring of spring constant K. A mass m hangs from the free end of the spring. The area of cross-section and Young.s modulus of the wire are A and Y respectivley. Find the time period with which the mass m will oscillate if it is slightly pulled down and released?
View SolutionOne end of a long metallic wire of length L is tied to the ceiling. The other end is tied to massless spring of spring constant K. A mass (m) hangs freely from the free end of the spring. The area of cross-section and young's modulus of the wire are A and Y respectively. If the mass is slightly pulled down and released it will oscillate with a time period T equal to
View SolutionOne end of a long metallic wire of length L is tied to the ceiling. The other end is tied to massless spring of spring constant K. A mass (m) hangs freely from the free end of the spring. The area of cross-section and young's modulus of the wire are A and Y respectively. If the mass is slightly pulled down and released it will oscillate with a time period T equal to
View SolutionOne end of a long mettalic wire of length L is tied to the ceiling. The other end is tied to massless spring of spring constant K. A mass M hangs freely from the free end of the spring. The area of cross-section and Young's modulus of the wire are A and Y respectively. If the mass is slightly pulled down and released, it will oscillate with a time period T equal to
View Solution

