If Poission's ratio σ is −12 for a material, then the material is
elastic fatigue
incompressible
compressible
None of these
The correct Answer is:B
To determine the nature of the material given that Poisson's ratio σ is −12, we can follow these steps:
1. Understanding Poisson's Ratio:
Poisson's ratio σ is defined as the negative ratio of transverse strain to axial strain. It indicates how much a material deforms in the lateral direction when subjected to axial stress.
2. Given Value:
We are given that σ=−12.
3. Relation Between Poisson's Ratio and Volume Change:
The change in volume dVV can be expressed in terms of Poisson's ratio as:
dVV=1+2σdLL
where dLL is the strain.
4. Substituting the Given Value:
Substitute σ=−12 into the equation:
dVV=1+2(−12)dLL
This simplifies to:
dVV=1−dLL
5. Analyzing the Expression:
If we assume that the material is undergoing a uniform deformation, we can set dLL=1 (which would imply maximum elongation):
dVV=1−1=0
This indicates that the volume change dV is zero, meaning the volume remains constant.
6. Bulk Modulus Relation:
The bulk modulus K is defined as:
K=−pdVV
Since dVV=0, this implies that:
K→∞
Therefore, the material is incompressible.
7. Conclusion:
Since the bulk modulus is infinite, we conclude that the material is incompressible.
Final Answer:
The material is incompressible.
---
Poisson's ratio σ is defined as the negative ratio of transverse strain to axial strain. It indicates how much a material deforms in the lateral direction when subjected to axial stress.
We are given that σ=−12.
The change in volume dVV can be expressed in terms of Poisson's ratio as:
dVV=1+2σdLL
where dLL is the strain.
Substitute σ=−12 into the equation:
dVV=1+2(−12)dLL
This simplifies to:
dVV=1−dLL
If we assume that the material is undergoing a uniform deformation, we can set dLL=1 (which would imply maximum elongation):
dVV=1−1=0
This indicates that the volume change dV is zero, meaning the volume remains constant.
The bulk modulus K is defined as:
K=−pdVV
Since dVV=0, this implies that:
K→∞
Therefore, the material is incompressible.
Since the bulk modulus is infinite, we conclude that the material is incompressible.
The material is incompressible.
Topper's Solved these Questions
Similar Questions
A: Lateral strain is directly proportional to the longitudinal strain within the elastic limit.
R:Poission ratio for a given material at a constant temperature is constant.
View SolutionWhen the length of a wire is increased by 5%, its radius decreases by 1%. The Poission's ratio for the material of the wire is
View Solution
Knowledge Check
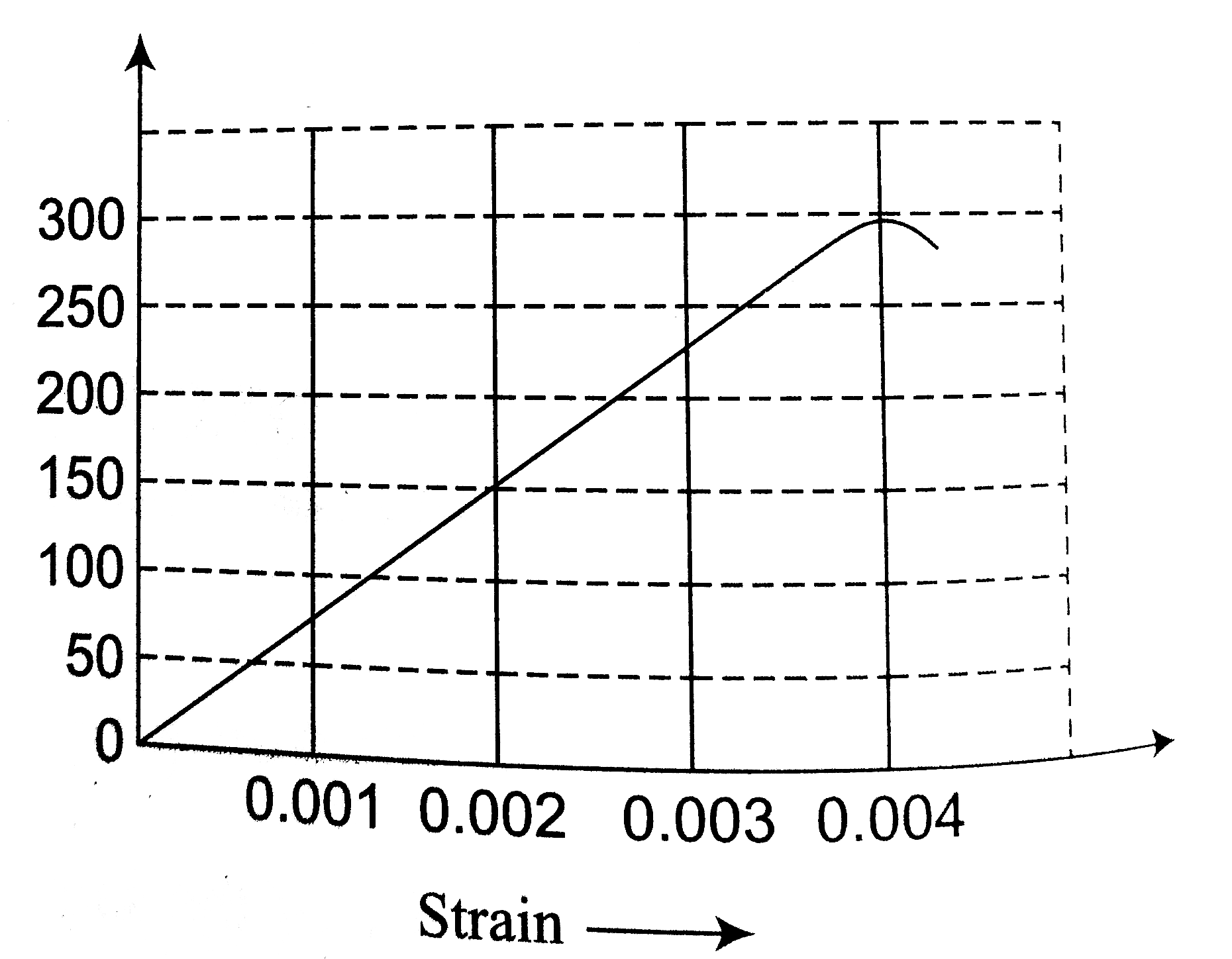
Figure shows the strain stress curve for a given material. The Young's modulus of the material isA5×109Nm−2B5×1010Nm−2C7.5×109Nm−2D7.5×1010Nm−2The Poisson's ratio of a material is 0.4. If a force is applied to a wire of this material, there is a decrease of cross-sectional area by 2%. The percentage increase in its length is
A3%B2.5%C1%D0.5%
If Young's modulus of elasticity Y for a material is one and half times its rigidity coefficient η,the Poisson's ratio σ will be
View SolutionThe intensity of magnetisation of a magnetic material is l . Now material is the cut such that volume of the material is halved, then new intensity of magnetization is
View SolutionIf a material loses electrons from its outermost shell, the material acquires a :
View SolutionThe speed of longitudinal mechanical wave in a material is 4300 m/s. young's modulus of the material is 15×109N/m2. What is the density of the material?
View SolutionThe temperature coefficient of resistivity of material is 0.0004/k. When the temperature of the material is increased by 50∘C, its resistivity increases by 2×10−8 ohm-m. The initial resistivity of the material in ohm-m is
View SolutionIn a radioactive material the activity at time t1 is R1 and at a later time t2, it is R2. If the decay constant of the material is λ, then
View Solution
