Two identical containers joned by a small pipe initially contain the same gas at pressue po and abosolute temperature To. One container is now mantained at the same temperature while the other is heated to 2T0. The commmon pressure of the gases will be
32po
43po
35po
2po
The correct Answer is:B
To solve the problem, we will use the ideal gas law and the concept of conservation of moles. Let's break down the solution step by step.
1. Identify the Initial Conditions:
- Both containers have the same gas with initial pressure P0 and absolute temperature T0.
- Let the volume of each container be V0.
2. Determine Moles in Each Container Initially:
- For Container 1 (maintained at T0):
n1=P0V0RT0
- For Container 2 (heated to 2T0):
n2=P0V0R(2T0)=P0V02RT0
3. Total Moles in the System:
- The total number of moles ntotal in the system is:
ntotal=n1+n2=P0V0RT0+P0V02RT0
- Simplifying this gives:
ntotal=P0V0RT0(1+12)=P0V0RT0⋅32=3P0V02RT0
4. Final Condition After Equilibrium:
- After reaching equilibrium, let the common pressure be P and the temperature of Container 1 remains T0 while Container 2 is at 2T0.
- The moles in each container at equilibrium can be expressed as:
- For Container 1:
n′1=PV0RT0
- For Container 2:
n′2=PV0R(2T0)=PV02RT0
5. Equating Total Moles:
- At equilibrium, the total moles must remain the same:
n′1+n′2=ntotal
- Substituting the expressions:
PV0RT0+PV02RT0=3P0V02RT0
6. Simplifying the Equation:
- Factor out V0RT0:
(P+P2)=3P02
- This simplifies to:
3P2=3P02
7. Solving for Common Pressure P:
- Multiply both sides by 23:
P=P0⋅43
Final Answer:
The common pressure of the gases after equilibrium is:
P=4P03
- Both containers have the same gas with initial pressure P0 and absolute temperature T0.
- Let the volume of each container be V0.
- For Container 1 (maintained at T0):
n1=P0V0RT0
- For Container 2 (heated to 2T0):
n2=P0V0R(2T0)=P0V02RT0
- The total number of moles ntotal in the system is:
ntotal=n1+n2=P0V0RT0+P0V02RT0
- Simplifying this gives:
ntotal=P0V0RT0(1+12)=P0V0RT0⋅32=3P0V02RT0
- After reaching equilibrium, let the common pressure be P and the temperature of Container 1 remains T0 while Container 2 is at 2T0.
- The moles in each container at equilibrium can be expressed as:
- For Container 1:
n′1=PV0RT0
- For Container 2:
n′2=PV0R(2T0)=PV02RT0
- At equilibrium, the total moles must remain the same:
n′1+n′2=ntotal
- Substituting the expressions:
PV0RT0+PV02RT0=3P0V02RT0
- Factor out V0RT0:
(P+P2)=3P02
- This simplifies to:
3P2=3P02
- Multiply both sides by 23:
P=P0⋅43
The common pressure of the gases after equilibrium is:
P=4P03
Topper's Solved these Questions
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - B medical entrance special format questions
14 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Match the columns
5 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Check point 14.4
25 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective
9 Videos
Similar Questions
Two idential container joined by a small pipe initially contain the same gas at pressure p0 and absolute temperature T0. One container is now maintained at the same temperature while the other is heated to 2T0. The common pressure of the gas
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionA cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless position. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is po and temperature is To, atmospheric pressure is also po Now the temperature of the gas is increased to 2T0, the tension in the wire will be

View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View SolutionTwo identical vessels contain helium and hydrogen gases at same temperature, then
View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure Pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below . The temperature of one of the bulbs is then raised to T2 . the final pressure Pf is
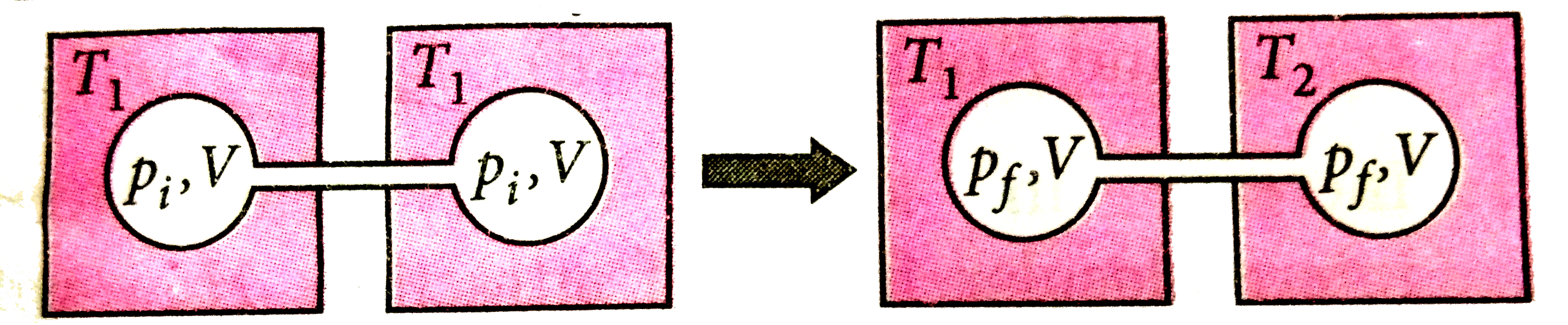
View Solution
A cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless pistons. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is P0 and temperature is T0, atmospheric pressure is also P0. Now the temperature of the gas is increased to 2T0, the tension in the wire will be
View SolutionConsider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas is container B is compressed to half of its original vlue adiabatically. The ratio of final pressure of gas of B to that of gas in A is
View SolutionTwo closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
View Solution

