The distance of moon form the earth is 3.8×105 km. Supposing that the eye is most sensitive to the ight of wavelength 550nm, the separation of two points on the moon that can be resolved by a 500cm
50m
55m
51m
60m
The correct Answer is:B
To solve the problem of determining the separation of two points on the moon that can be resolved by the human eye, we will use the formula for resolving power. Here are the step-by-step calculations:
Step 1: Understand the Given Data
- Distance of the moon from Earth, D=3.8×105 km
- Wavelength of light, λ=550 nm
Step 2: Convert Units
1. Convert the distance from kilometers to meters:
D=3.8×105 km=3.8×105×1000 m=3.8×108 m
2. Convert the wavelength from nanometers to meters:
λ=550 nm=550×10−9 m
Step 3: Use the Resolving Power Formula
The formula for the minimum resolvable separation d is given by:
d=1.22⋅D⋅λD
Substituting the values we have:
d=1.22⋅(3.8×108)⋅(550×10−9)D
Step 4: Calculate the Resolving Power
Now we can calculate d:
d=1.22⋅(3.8×108)⋅(550×10−9)1
Calculating the product:
d=1.22⋅3.8⋅550×10−1=1.22⋅3.8⋅0.00000055
Calculating this gives:
d≈55 meters
Conclusion
The separation of two points on the moon that can be resolved by the human eye is approximately 55 meters.
- Distance of the moon from Earth, D=3.8×105 km
- Wavelength of light, λ=550 nm
1. Convert the distance from kilometers to meters:
D=3.8×105 km=3.8×105×1000 m=3.8×108 m
2. Convert the wavelength from nanometers to meters:
λ=550 nm=550×10−9 m
The formula for the minimum resolvable separation d is given by:
d=1.22⋅D⋅λD
Substituting the values we have:
d=1.22⋅(3.8×108)⋅(550×10−9)D
Now we can calculate d:
d=1.22⋅(3.8×108)⋅(550×10−9)1
Calculating the product:
d=1.22⋅3.8⋅550×10−1=1.22⋅3.8⋅0.00000055
Calculating this gives:
d≈55 meters
The separation of two points on the moon that can be resolved by the human eye is approximately 55 meters.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
22 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
Assertion The formula connecting u, v and f for a spherical mirror is valid only for mirrors sizes which are very small compared to their radii of curvature.
Reason Laws of reflection are stricity valid for plane surface, but not for large spherical.
View SolutionThe half-life of a radioactive substance is 30 minutes, The time (in minutes) taken between 40% decay and 85% decay of the same radioactive substance is.
View SolutionA point source of light S is placed at a distance 10 cm in front of the centre of a mirror of width 20 cm suspended vertically on a wall. An insect walks with a speed 10cm/s in front of the mirror along a line parallel to the mirror at a distance 20 cm from it as shown in figure. find the maximum time during which the insect can see the image of the source S in the mirror.
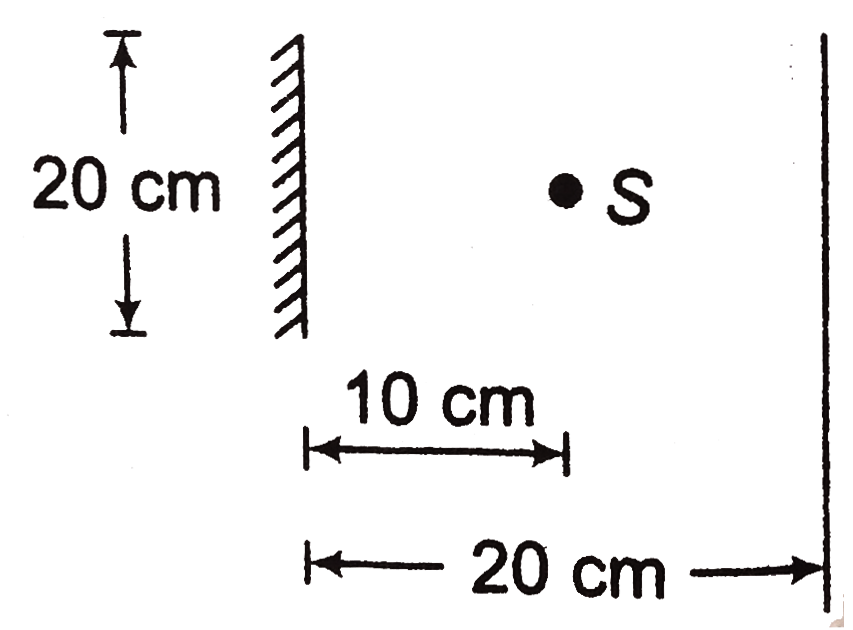
View SolutionCalculate the separation of two points on moon that can be resolve using 600cm telescope. Given distance of moon from earth =3.8×1010cm. The wavelength most sensitive to eye is 5.5×10−5cm.
View SolutionThe distance between earth and moon is about 3.8×105km. At what point or points will the gravitational field strength of earth-moon system be zero? Given mass of earth is 81 times the moon's mass.
View SolutionThe diameter of the moon is 3.5xx10^(3)km and its distance from the earth is 3.8xx10^(5) km . It is seen by a telescope having the focal length of the objective and the eye-piece as 4m and 10cm respectively. The diameter of the image of the moon will be approximately
View SolutionThe distance of the moon from earth is 3.8 xx 10^(5) km . The eye is most sensitive to light of wavelength 5500 Å . The separation of two points on the moon that can be resolved by a 500 cm telescope will be
View SolutionThe distance of moon form the earth is 3.8xx10^(5) km. Supposing that the eye is most sensitive to the ight of wavelength 550nm, the separation of two points on the moon that can be resolved by a 500cm
View Solutionचंद्रमा का द्रव्यमान 7.36×1022 kg तथा धरती का द्रव्यमान 6×1024 kg है | इनके बीच की दूरी 3.8×105 km है | चंद्रमा का भार बताएँ |
View Solutionएक अवतल दर्पण की फोकस-दुरी 7.6m है। इसके द्वारा चंद्रमा के प्रतिबिंब का व्यास निकाले। चंद्रमा का व्यास 3450km है तथा धरती से इसकी दुरी 3.8×105km है।
View Solutionमाना पृथ्वी की चन्द्रमा से दुरी 38400 किमी है तथा चन्द्रमा द्वारा पृथ्वी पर किसी व्यक्ति की आँख पर मापा गया कोण 31' है । चन्द्रमा की त्रिज्या ज्ञात कीजिए ।
View SolutionThe diameter of the moon is 3450 km and its distance from the earth is 3.8xx10^(5)km. What will be the diameter of the image of the moon formed by a convex mirror of focal length 7.6 m ?
View SolutionIf aperture diameter of telescope is 10m and distance Moon and Earth is 4 xx 10^(5) Km . With wavelength of lightis 5500 Å . The minimum separation between objects on surface of Moon, so that they are just resolved is close to :
View SolutionA telescope of diameter 500 cm is used to resolve two points on the moon. Calculate the separation between the points . Take distance of the moon from the Earth =4×1010cm, and wavelength of light most sensitive to eye =5.5×10−5cm.
View Solutionपृथ्वी से चन्द्रमा 3.8×105 किमी. है। यदि पृथ्वी का द्रव्यमान 6×1024 किग्रा. है तो चन्द्रमा की कक्षीय चाल क्या है ?
View Solution

