According to Bohrr model of hydrogen atom, only those orbit are permissible which satisfy the condition
mv=nh
mv2r=n(h2π)
mvr=n(h2π)
mvr2=n(h2π)
The correct Answer is:C
To solve the question regarding the permissible orbits in the Bohr model of the hydrogen atom, we follow these steps:
1. Understanding the Bohr Model:
- The Bohr model of the hydrogen atom states that electrons move in fixed orbits around the nucleus and that these orbits are quantized.
2. Angular Momentum Quantization:
- According to Bohr's theory, the angular momentum (L) of an electron in a hydrogen atom is quantized. This means that it can only take on certain discrete values.
3. Expression for Angular Momentum:
- The angular momentum (L) of an electron in orbit is given by the formula:
L=mvr
where:
- m is the mass of the electron,
- v is the velocity of the electron,
- r is the radius of the orbit.
4. Quantization Condition:
- Bohr postulated that the angular momentum is quantized and can be expressed as:
L=nh2π
where:
- n is a positive integer (principal quantum number),
- h is Planck's constant.
5. Setting the Equations Equal:
- By equating the two expressions for angular momentum, we have:
mvr=nh2π
6. Conclusion:
- Thus, the condition that must be satisfied for permissible orbits in the hydrogen atom according to the Bohr model is:
mvr=nh2π
- Therefore, the correct option is:
Option 3: mvr=nh2π
- The Bohr model of the hydrogen atom states that electrons move in fixed orbits around the nucleus and that these orbits are quantized.
- According to Bohr's theory, the angular momentum (L) of an electron in a hydrogen atom is quantized. This means that it can only take on certain discrete values.
- The angular momentum (L) of an electron in orbit is given by the formula:
L=mvr
where:
- m is the mass of the electron,
- v is the velocity of the electron,
- r is the radius of the orbit.
- Bohr postulated that the angular momentum is quantized and can be expressed as:
L=nh2π
where:
- n is a positive integer (principal quantum number),
- h is Planck's constant.
- By equating the two expressions for angular momentum, we have:
mvr=nh2π
- Thus, the condition that must be satisfied for permissible orbits in the hydrogen atom according to the Bohr model is:
mvr=nh2π
- Therefore, the correct option is:
Option 3: mvr=nh2π
Topper's Solved these Questions
Similar Questions
In Column I physical quantities corresponding to hydrogen and hydrogen like atom are given. In column II, powers of principal quantum number n are givem on which thosee physical quantities depend. Match the two columns.
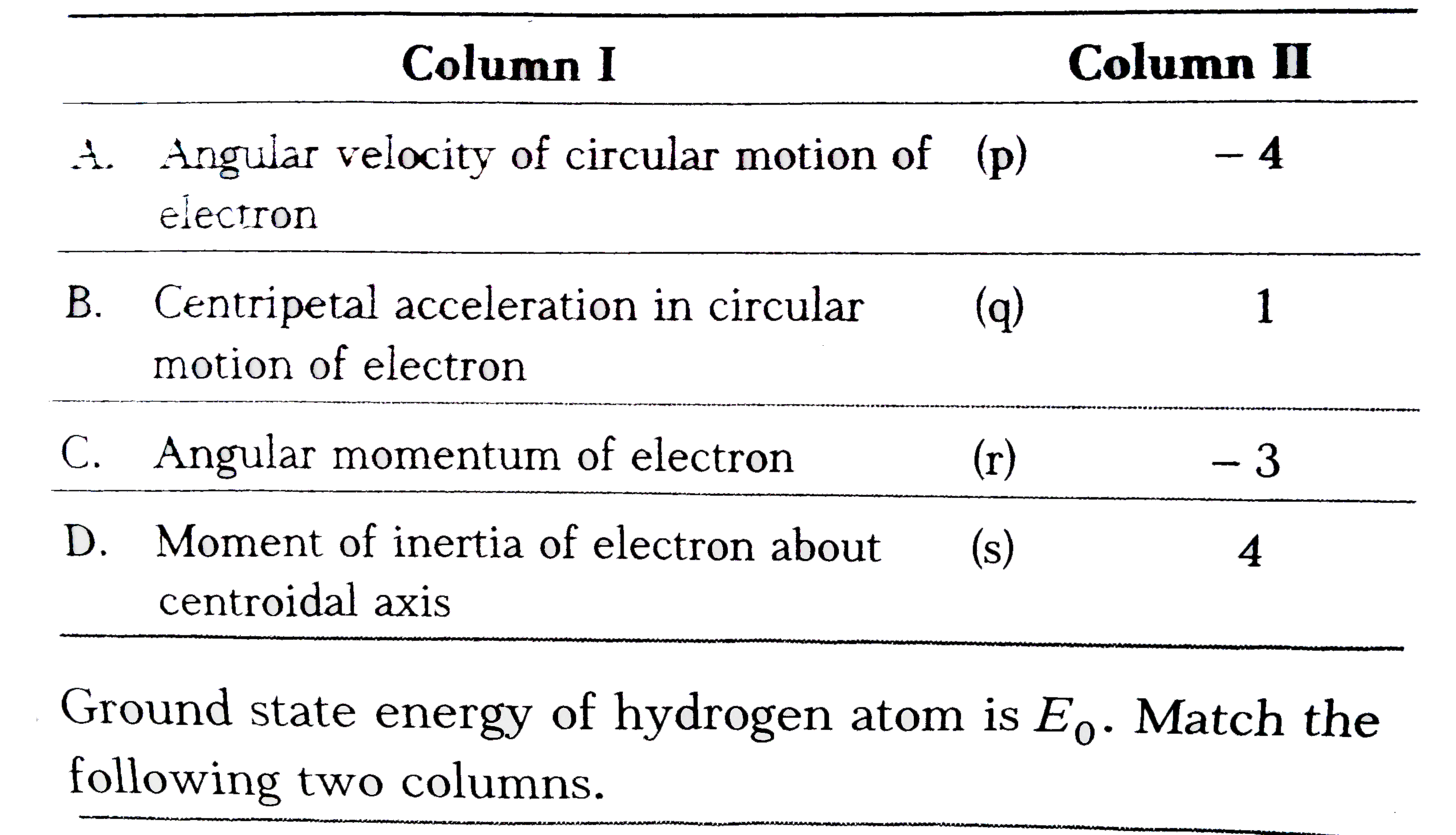
View SolutionIn the given arrangement, the loop is moved with consisant velocity in uniform magnetic field B in a restricted a region of width a. The time for which the emf is induced in the cirucit is

View SolutionIn the circuit shown as potential difference of 60V is appliled across AB. The potential difference between the points M and N is
View SolutionIn Bohr model of the hydrogen atom, the lowest orbit corresponds to
View SolutionAccording to bohr model, the diameter or first orbit of hydrogen atom will be
View SolutionAccording to Bohr's Model of hydrogen atom
View SolutionAccording to Bohrr model of hydrogen atom, only those orbit are permissible which satisfy the condition
View SolutionAccording to Bohr's atomic model, electrons revolve in ______ orbits.
View SolutionAccording to Bohr's model , the ratio of the energies of the electron in the first orbit of hydrogen atom and He^(+) atom is
View Solutionबोर मॉडल के अनुसार हाइड्रोजन परमाणु की स्थायी कक्षाओं के लिये त्रिज्या के लिये सूत्र स्थापित कीजिये तथा सिध्द कीजिये कि हाइड्रोजन परमाणु में स्थायी कक्षाओं की त्रिज्याओं का अनुपात 1 : 4 : 9 होता है ।
View SolutionAccording to Bohr model , radius of the first orbit of hydrogen atom is r1 then the radii of second , third and fouth orbitals in term of r1 are
View SolutionAccording to Bohr's theory, hydrogen atom for an electron in the nth permissible orbit
View SolutionAccording to Bohr's quantum condition an electron in hydrogen and hydrogen like atoms can revolve in those stable orbits in which its momentum is an integer multiple of Planck's constant.
View SolutionIn Bohr model of the hydrogen atom, the lowest orbit corresponds to
View SolutionAccording to Bohr only those orbit are permissible for which the angular momentum of an electron is integral multiple of:
View Solution

