एक सरल रेखा के अनुदि । संचरित तीन तरंगे निम्न है -
2Asin(kx−ωt+π3),√3Acos(kx−ωt−π3)2√3Acos(kx−ωt+π3)
(2+3√3A)
√31A
√19A
(2−√3A)A
The correct Answer is:C
तरंगो को फेजर आरेख का उपयोग करते हुए जोड़ा जा सकता है।
टॉपर्स ने हल किए ये सवाल
समान प्रश्न
दो सरल ऊर्जा गतियों के समीकरण x1=5sin(2πt+π/4),x2=5.√2(sin2πt+cos2πt) है| इनके आयामों का अनुपात और कालांतर होगा-
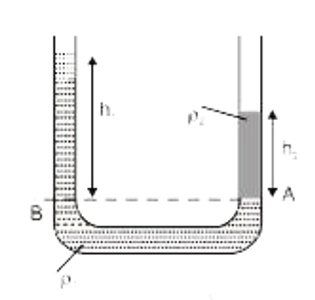
View SolutionU-नलिका में दो अमिश्रणीय द्रव जिनके घनत्व p1=1.0×103kg/m3 तथा p2=3.0×103kg/m3 है, भरे हुए हैं। उभयनिष्ठ अन्तः पृष्ठ से द्रवों की ऊँचाईयों का अनुपात h1h2 ज्ञात कीजिए।
View SolutionWhich of the following equations can form stationary waves? (i) y= A sin (omegat - kx) (ii) y= A cos (omegat - kx) (iii) y= A sin (omegat + kx) (iv) y= A cos (omegat - kx) .
View SolutionWhich two of the given transverse waves will give stationary wave when get superimposed? z_(1) = a cos (kx-omegat) " "(A) z_(2) = a cos (kx +omegat) " "(B) z_(3) = a cos (ky - omegat) " "(C )
View SolutionTwo SHM's are represented by y = a sin (omegat - kx) and y = b cos (omegat - kx) . The phase difference between the two is :
View SolutionThe phase difference between the waves y=acos(ωt+kx)andy=asin(ωt+kx+π2) is
View Solutionचार प्रगामी तरंगों W1,W2,W3 एवं W4 के समीकरण हैं, क्रमश: y=A0sin(kx−ωt),y=A0sin(kx+ωt),y=A0cos(kx−ωt) तथा y=A0cos(kx+ωt0) । अप्रगामी तरंग बन सकती है
View SolutionTwo waves are represented by Y_1=a_1 cos (omegat-kx) and Y-2 =a_2 sin (omegat-kx+pi//3) Then the phase difference between them is-
View Solutionदो तरंगो y=acos(ωt+kx) तथा y=asin(ωt+kx) में कलांतर बताइये।
View SolutionTwo waves y_(1) = a sin (omegat - kx) and y_(2) = a cos(omegat - kx) superimpose at a point :
View SolutionOn the superposition of the two waves given as y1=A0sin(ωt−kx) and y2=A0cos(ωt−kx+π6) , the resultant amplitude of oscillations will be
View Solutiony1=4sin(ωt+kx)y2=−4cos(ωt+kx) எனில் கட்ட வேறுபாடு?
View SolutionWhich of the following equations can form stationary waves? (i) y= A sin (omegat - kx) (ii) y= A cos (omegat - kx) (iii) y= A sin (omegat + kx) (iv) y= A cos (omegat - kx) .
View SolutionY1=10sin(ωt−kx) तथा Y2=5[sin(ωt–kx)+√3cos(kx−ωt)] एक ही माध्यम में संचरित यांत्रिक तरंगे है तो इनकी तीव्रताओं का अनुपात क्या होगा।
View SolutionWhich two of the given transverse waves will give stationary wave when get superimposed?
z1=acos(kx−ωt) (A)
z2=acos(kx+ωt) (B)
z3=acos(ky−ωt) (C)
View Solution

