In a ΔABC , Median AD perpendicular to side BC . Find the value of tanA/tanB
1
3
0
-2
To solve the problem, we will follow these steps:
Step 1: Understand the Geometry
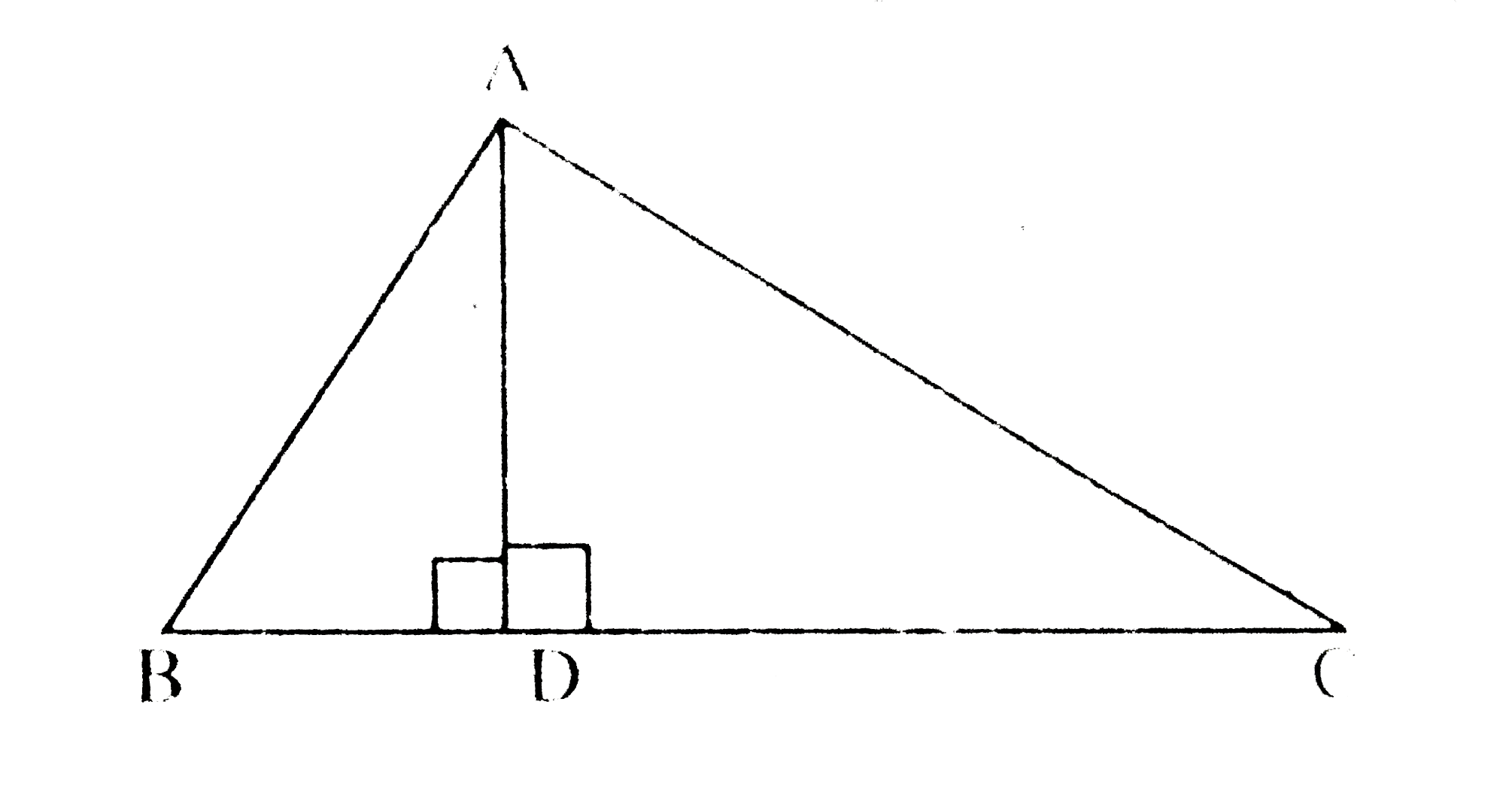
In triangle ABC, median AD is perpendicular to side BC. This means that AD divides BC into two equal segments, BD and DC.
Step 2: Label the Angles
Let ∠A=A, ∠B=B, and ∠C=C. Since AD is perpendicular to BC, we have ∠ADB=90∘.
Step 3: Use the Exterior Angle Theorem
In triangle ABD, we can express ∠ADB as 90∘. Therefore, the angle ∠BAD can be expressed as A−90∘ (let's denote this angle as θ).
Step 4: Apply the Pythagorean Theorem
In triangle ABD:
AB2+AD2=BD2
Since AD is a median, we can express BD as BC2.
Step 5: Set Up the Equation
Using the median length formula:
BD2=14(2AC2+2AB2−BC2)
Substituting BD=BC2:
AB2+AD2=BC24
Step 6: Rearranging the Equation
Rearranging gives:
AB2+AD2=14(2AC2+2AB2−BC2)
This leads to:
4AB2+4AD2=2AC2+2AB2−BC2
Step 7: Simplifying
Combining like terms leads to:
2AB2+4AD2+BC2=2AC2
Step 8: Find the Value of tanAtanB
Using the definitions of tangent:
tanA=sinAcosA,tanB=sinBcosB
Thus,
tanAtanB=sinA⋅cosBsinB⋅cosA
Step 9: Substitute Values
Using the sine rule:
sinAsinB=BCAC
And for cosines, we can use the cosine rule.
Step 10: Final Calculation
After substituting and simplifying, we find that:
tanAtanB=−2
Conclusion
The value of tanAtanB is −2.
---
In triangle ABC, median AD is perpendicular to side BC. This means that AD divides BC into two equal segments, BD and DC.
Let ∠A=A, ∠B=B, and ∠C=C. Since AD is perpendicular to BC, we have ∠ADB=90∘.
In triangle ABD, we can express ∠ADB as 90∘. Therefore, the angle ∠BAD can be expressed as A−90∘ (let's denote this angle as θ).
In triangle ABD:
AB2+AD2=BD2
Since AD is a median, we can express BD as BC2.
Using the median length formula:
BD2=14(2AC2+2AB2−BC2)
Substituting BD=BC2:
AB2+AD2=BC24
Rearranging gives:
AB2+AD2=14(2AC2+2AB2−BC2)
This leads to:
4AB2+4AD2=2AC2+2AB2−BC2
Combining like terms leads to:
2AB2+4AD2+BC2=2AC2
Using the definitions of tangent:
tanA=sinAcosA,tanB=sinBcosB
Thus,
tanAtanB=sinA⋅cosBsinB⋅cosA
Using the sine rule:
sinAsinB=BCAC
And for cosines, we can use the cosine rule.
After substituting and simplifying, we find that:
tanAtanB=−2
The value of tanAtanB is −2.
Topper's Solved these Questions
Similar Questions
The LCM of two numbers is 864 and their HCF is 144.If one of the number is 288,the other number is:
View SolutionRam can do a work in 15 days, while Ram and Shiva work together they can complete the work in 10 days, in how many days Shiva can alone do the same work?
View SolutionIn a ΔABC, prove that : tanA+tanB+tanC=tanAtanBtanC
View SolutionIn ΔABC,
tanA+tanB+tanC=tanAtanBtanC
View SolutionIf A+B=45∘, then find the value of tanA+tanB+tanAtanB.
View SolutionΔABC में यदि भुजा AD भुजा BC पर लम्ब है और AD2=BD×CD सिद्ध कीजिए कि ΔABC एक समकोण त्रिभुज है।
View Solutionयदि किसी त्रिभुज ABC की माध्यिका AD भुजा AB के लम्ब रूप हो , तो सिद्ध कीजिए कि tanA+2tanB=0
View Solutionसिद्ध करें की ΔABC समद्विबाहु त्रिभुज होगा जिसमें AB = AC यदि और केवल यदि
माध्यिका AD भुजा BC पर लम्ब हो |
View Solutionयदि किसी त्रिभुज ABC की माध्यिका AD भुजा AB के लम्ब रूप हो , तो सिद्ध कीजिए कि tanA+2tanB=0
View Solutionसिद्ध कीजिये की ΔABC समद्विबाहु त्रिभुज होगा यदि
मध्यिका AD, आधार BC पर लंब हो।
View SolutionIn a ΔABC,atanA+btanB+CtanC is equal to
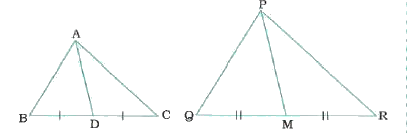
View SolutionSides AB and BC and median AD of a DeltaABC are respectively proportional to sides PQ and QR and median PM of ΔPQR (see the given figure). Show that ΔABC~ΔPQR.
View SolutionIn a ΔABC ∑(cotA+cotBtanA+tanB) is equal to
View Solutionसिद्ध करें कि ΔABC एक समद्विबाहु त्रिभुज है यदि माध्यिका AD, BC पर लम्ब है।
View SolutionIn ΔABC,
tanA+tanB+tanC=tanAtanBtanC
View Solution