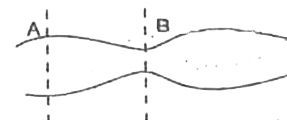
State and prove Bernouli's theorem.
Step-by-Step Solution for Bernoulli's Theorem
Step 1: State Bernoulli's Theorem
Bernoulli's theorem states that for an ideal fluid flowing in a streamline motion, the total mechanical energy per unit volume remains constant. This can be expressed mathematically as:
P+12ρv2+ρgh=constant
where:
- P = pressure energy per unit volume,
- 12ρv2 = kinetic energy per unit volume,
- ρgh = potential energy per unit volume,
- ρ = density of the fluid,
- v = velocity of the fluid,
- g = acceleration due to gravity,
- h = height above a reference level.
Step 2: Consider a Fluid Flow in a Pipe
Let’s consider a fluid flowing through a pipe with varying cross-sectional areas. Let point 1 be at height h1 with pressure P1 and velocity v1, and point 2 be at height h2 with pressure P2 and velocity v2.
Step 3: Apply the Principle of Conservation of Energy
According to the conservation of energy, the work done on the fluid as it moves from point 1 to point 2 can be expressed in terms of the changes in kinetic energy, potential energy, and pressure energy.
Step 4: Write the Energy Equation
The work done by pressure forces can be expressed as:
P1+12ρv21+ρgh1=P2+12ρv22+ρgh2
Step 5: Rearranging the Equation
Rearranging the equation gives us:
P1+12ρv21+ρgh1=P2+12ρv22+ρgh2
This indicates that the sum of the pressure energy, kinetic energy, and potential energy at point 1 is equal to that at point 2.
Step 6: Conclusion
Thus, we conclude that the total mechanical energy of the fluid remains constant along a streamline, which is the essence of Bernoulli's theorem.
Bernoulli's theorem states that for an ideal fluid flowing in a streamline motion, the total mechanical energy per unit volume remains constant. This can be expressed mathematically as:
P+12ρv2+ρgh=constant
where:
- P = pressure energy per unit volume,
- 12ρv2 = kinetic energy per unit volume,
- ρgh = potential energy per unit volume,
- ρ = density of the fluid,
- v = velocity of the fluid,
- g = acceleration due to gravity,
- h = height above a reference level.
Let’s consider a fluid flowing through a pipe with varying cross-sectional areas. Let point 1 be at height h1 with pressure P1 and velocity v1, and point 2 be at height h2 with pressure P2 and velocity v2.
According to the conservation of energy, the work done on the fluid as it moves from point 1 to point 2 can be expressed in terms of the changes in kinetic energy, potential energy, and pressure energy.
The work done by pressure forces can be expressed as:
P1+12ρv21+ρgh1=P2+12ρv22+ρgh2
Rearranging the equation gives us:
P1+12ρv21+ρgh1=P2+12ρv22+ρgh2
This indicates that the sum of the pressure energy, kinetic energy, and potential energy at point 1 is equal to that at point 2.
Thus, we conclude that the total mechanical energy of the fluid remains constant along a streamline, which is the essence of Bernoulli's theorem.
Topper's Solved these Questions
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SHORT ANSWER QUESTIONS
36 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - VERY SHORT ANSWER QUESTIONS
8 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
16 Videos
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)
21 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
Similar Questions
Knowledge Check
Applications of Bernoulli's theorem can be seen in
A1. dynamic lift of aeroplaneB2. hydraulic pressC3. helicopterD4. none of these
State basic proportionality theorem and its converse.
View Solution(a) State the basic proportionality theorem.
(b) state the mid-point theorem.
© State pythagoras theorem.
(d) State the conditions for similarity of two triangles.
View SolutionState (i) parallel axes theorem and (ii) perpendicular axes theorem.
View SolutionExplain Torricelli's theorem
View SolutionState Bayes Theorem
View SolutionState and prove law of equipartition of energy.
View SolutionState and prove the law of conservation of angular momentum.
View Solution