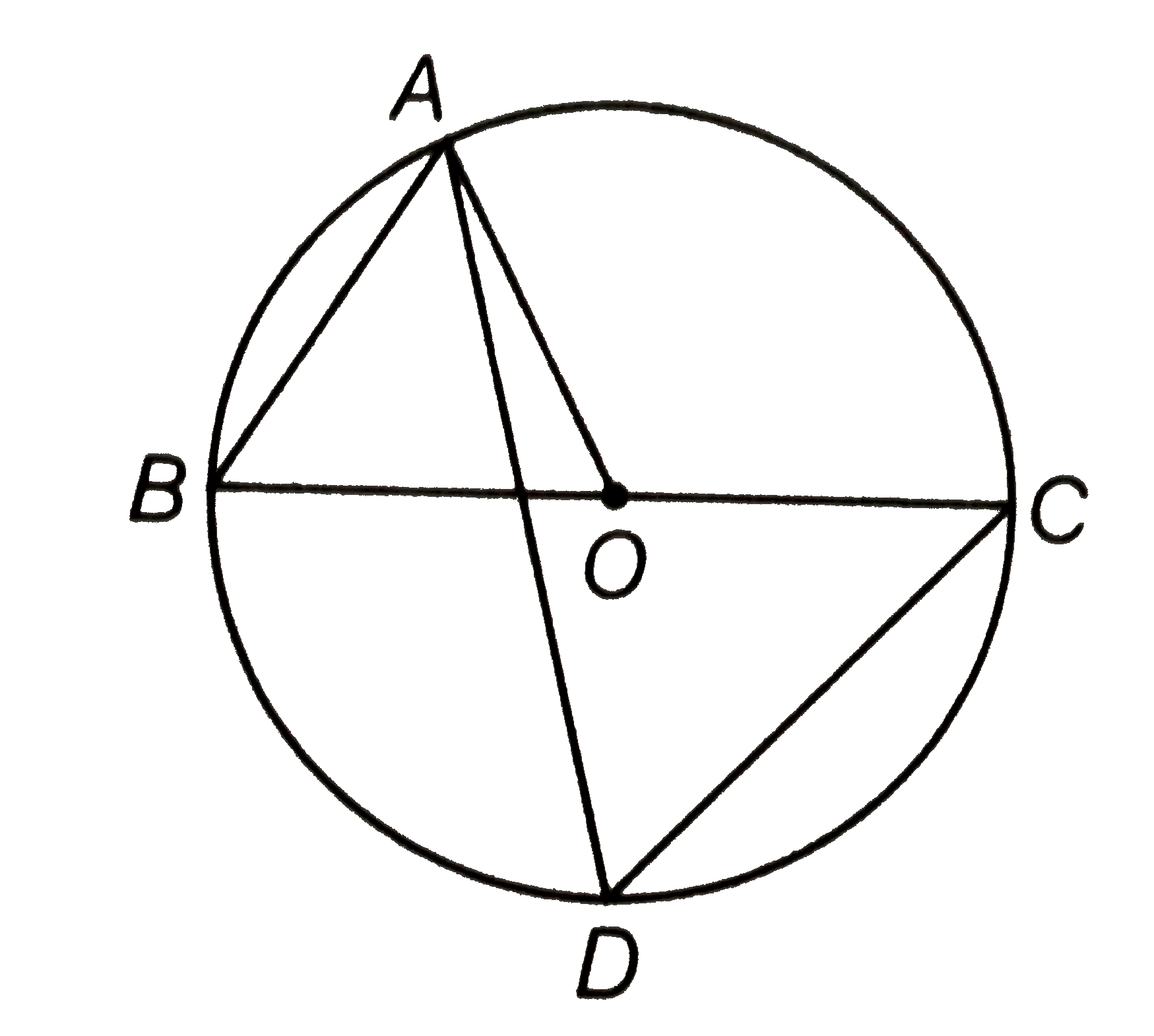
Points A,B,C and D are concyclic. BC is the diameter and O is the centre of the circle, ∠BAO=69∘ find ∠DAO+∠DCO
A)138
B)111
C)121
D)none of these
The correct Answer is:B
To solve the problem, we need to find the sum of angles ∠DAO+∠DCO given that points A, B, C, and D are concyclic, with BC as the diameter and O as the center of the circle. We know that ∠BAO=69∘.
1. Identify the Circle and Points:
- Draw a circle with points A, B, C, and D on its circumference.
- Mark BC as the diameter of the circle, and O as the center of the circle.
2. Label the Angles:
- We know that ∠BAO=69∘.
3. Determine ∠ABO:
- Since OA and OB are radii of the circle, triangle AOB is isosceles.
- Therefore, ∠ABO=∠OAB=69∘.
4. Calculate ∠AOB:
- The sum of angles in triangle AOB is 180∘.
- Thus, ∠AOB=180∘−∠BAO−∠ABO=180∘−69∘−69∘=42∘.
5. Find ∠DAB:
- Since A, B, C, D are concyclic and BC is the diameter, ∠BAC=90∘ (angle subtended by diameter).
- Therefore, ∠DAB+∠BAC=180∘ (opposite angles in cyclic quadrilateral).
- Hence, ∠DAB=180∘−90∘=90∘.
6. Calculate ∠DCO:
- Since ∠DAB=90∘ and ∠BAO=69∘, we can find ∠DAB using the cyclic property.
- ∠DCO=∠DAB−∠BAO=90∘−69∘=21∘.
7. Find ∠DAO+∠DCO:
- We know ∠DAO=∠DAB=90∘.
- Therefore, ∠DAO+∠DCO=90∘+21∘=111∘.
Final Answer:
Thus, ∠DAO+∠DCO=111∘.
---
- Draw a circle with points A, B, C, and D on its circumference.
- Mark BC as the diameter of the circle, and O as the center of the circle.
- We know that ∠BAO=69∘.
- Since OA and OB are radii of the circle, triangle AOB is isosceles.
- Therefore, ∠ABO=∠OAB=69∘.
- The sum of angles in triangle AOB is 180∘.
- Thus, ∠AOB=180∘−∠BAO−∠ABO=180∘−69∘−69∘=42∘.
- Since A, B, C, D are concyclic and BC is the diameter, ∠BAC=90∘ (angle subtended by diameter).
- Therefore, ∠DAB+∠BAC=180∘ (opposite angles in cyclic quadrilateral).
- Hence, ∠DAB=180∘−90∘=90∘.
- Since ∠DAB=90∘ and ∠BAO=69∘, we can find ∠DAB using the cyclic property.
- ∠DCO=∠DAB−∠BAO=90∘−69∘=21∘.
- We know ∠DAO=∠DAB=90∘.
- Therefore, ∠DAO+∠DCO=90∘+21∘=111∘.
Thus, ∠DAO+∠DCO=111∘.
Topper's Solved these Questions
Similar Questions
The domain of the function f(x)=x is :
View SolutionThe value of log 6 is equal to:
View SolutionIf a+b+c=13 , a2+b2+c2=69 , then find ab+bc+ca . −50 (b) 50 (c) 69 (d) 75
View SolutionO केंद्र वाले वृत्त में, AB वृत्त का व्यास हे| यदि ∠AOE=150∘, ∠DAO=51∘ हे, तब ∠CBE का मन ज्ञात करे?

View SolutionIn figure, BC is a diameter of the circle and ∠BAO=60∘. Then,∠ADCis equal to
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionABCD is a parallelogram. A circle passing through C and D intersects AD and BC at the points E and F. Prove that the four points E, A, B, F are concyclic.
View SolutionAOB is a diameter of a circle with centre O and C is any point on the circle, joining A, C, B, C, and O, C, prove that
tan∠ABC=cot∠ACO
View SolutionIn circle AOD is diameter with centre of circle O and AB,BC,CD are equal chord then angle suntened by chord BC at centre is
View SolutionO is the centre of the circle passing through the points A, B and C such that ∠BAO=30∘,∠BCO=40∘and∠AOC=x∘ . What is the value of x ?
View SolutionIn figure, BC is a diameter of the circle and ∠BAO=60∘. Then,∠ADCis equal to

View SolutionAB is a diameter of a circle with centre O and radius OD is perpendicular to AB. If C is any point on arc DB, find ∠BAD and ∠ACD.
View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=500, find ∠AOC
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionAB is a diameter and AC is a chord of a circle with centre O such that ∠BAC=30∘. The tangent at C intersects AB at a point D. Prove that BC=BD.
View Solution
