250 students appeared in MOCK CAT consisting of three sections viz. Maths, Data Interpretation (DI) and English. 20 students did not qualify any of the three sections and 66 students qualified all the three sections, 24 students did not qualify DI only. 12 did not qualify DI and Maths only. Those who qualified Maths only exceeded those who did not qualify any of the section by 16. Those who did not qualify Maths only exceeded those who did not qualify only DI and Maths by 8. Those who did not qualify English only were twice the number of students who did not qualify Maths only. Find the number of students who has qualified atleast two sections.
To solve the problem step by step, we will define variables for each group of students based on their qualifications in the three sections: Maths (M), Data Interpretation (DI), and English (E).
1. Define Variables:
- Let x be the number of students who qualified only Maths.
- Let y be the number of students who qualified only DI.
- Let z be the number of students who qualified only English.
- Let a be the number of students who qualified both Maths and DI but not English.
- Let b be the number of students who qualified both Maths and English but not DI.
- Let c be the number of students who qualified both DI and English but not Maths.
- Let d be the number of students who qualified all three sections (given as 66).
- We know that 20 students did not qualify any section.
2. Total Students:
The total number of students is given as 250. Therefore, we can write the equation:
x+y+z+a+b+c+d+20=250
Substituting d=66:
x+y+z+a+b+c+66+20=250
Simplifying gives:
x+y+z+a+b+c=164(Equation 1)
3. Students Not Qualifying DI:
We know that 24 students did not qualify DI only, meaning they either did not qualify Maths or English or both. This can be expressed as:
20+z+x+12+a+b=24
Rearranging gives:
z+x+a+b=4(Equation 2)
4. Students Not Qualifying DI and Maths:
It is given that 12 students did not qualify DI and Maths only. This means:
c=12(Equation 3)
5. Students Qualifying Maths Only:
The number of students who qualified Maths only exceeds those who did not qualify any section by 16:
x=20+16=36(Equation 4)
6. Students Not Qualifying Maths Only:
The number of students who did not qualify Maths only exceeds those who did not qualify only DI and Maths by 8. The number of students who did not qualify only DI and Maths is 12:
y+c+z+20=12+8
Therefore:
y+z+20=20⇒y+z=0(Equation 5)
7. Students Not Qualifying English Only:
Those who did not qualify English only were twice the number of students who did not qualify Maths only. The number of students who did not qualify Maths only is:
20+z+y+12+a+b=20+0+12+a+b=32
Therefore:
2×32=64⇒c=64(Equation 6)
8. Substituting Values:
Now we can substitute the known values into the equations:
- From Equation 4: x=36
- From Equation 3: c=12
- From Equation 5: y=0 and z=0
Substitute these into Equation 1:
36+0+0+a+b+12+66+20=250
Simplifying gives:
a+b=164−36−12−66−20=34
9. Finding Students Qualifying at Least Two Sections:
Students qualifying at least two sections are those who qualified:
- Both Maths and DI (a)
- Both Maths and English (b)
- Both DI and English (c)
- All three sections (d)
Therefore:
At least two sections=a+b+c+d=a+b+12+66
Since a+b=34:
=34+12+66=112
Thus, the number of students who qualified at least two sections is 112.
- Let x be the number of students who qualified only Maths.
- Let y be the number of students who qualified only DI.
- Let z be the number of students who qualified only English.
- Let a be the number of students who qualified both Maths and DI but not English.
- Let b be the number of students who qualified both Maths and English but not DI.
- Let c be the number of students who qualified both DI and English but not Maths.
- Let d be the number of students who qualified all three sections (given as 66).
- We know that 20 students did not qualify any section.
The total number of students is given as 250. Therefore, we can write the equation:
x+y+z+a+b+c+d+20=250
Substituting d=66:
x+y+z+a+b+c+66+20=250
Simplifying gives:
x+y+z+a+b+c=164(Equation 1)
We know that 24 students did not qualify DI only, meaning they either did not qualify Maths or English or both. This can be expressed as:
20+z+x+12+a+b=24
Rearranging gives:
z+x+a+b=4(Equation 2)
It is given that 12 students did not qualify DI and Maths only. This means:
c=12(Equation 3)
The number of students who qualified Maths only exceeds those who did not qualify any section by 16:
x=20+16=36(Equation 4)
The number of students who did not qualify Maths only exceeds those who did not qualify only DI and Maths by 8. The number of students who did not qualify only DI and Maths is 12:
y+c+z+20=12+8
Therefore:
y+z+20=20⇒y+z=0(Equation 5)
Those who did not qualify English only were twice the number of students who did not qualify Maths only. The number of students who did not qualify Maths only is:
20+z+y+12+a+b=20+0+12+a+b=32
Therefore:
2×32=64⇒c=64(Equation 6)
Now we can substitute the known values into the equations:
- From Equation 4: x=36
- From Equation 3: c=12
- From Equation 5: y=0 and z=0
36+0+0+a+b+12+66+20=250
Simplifying gives:
a+b=164−36−12−66−20=34
Students qualifying at least two sections are those who qualified:
- Both Maths and DI (a)
- Both Maths and English (b)
- Both DI and English (c)
- All three sections (d)
At least two sections=a+b+c+d=a+b+12+66
Since a+b=34:
=34+12+66=112
Topper's Solved these Questions
Similar Questions
250 students appeared in MOCK CAT consisting of three sections viz. Maths, Data Interpretation (DI) and English. 20 students did not qualify any of the three sections and 66 students qualified all the three sections, 24 students did not qualify DI only. 12 did not qualify DI and Maths only. Those who qualified Maths only exceeded those who did not qualify any of the section by 16. Those who did not qualify Maths only exceeded those who did not qualify only DI and Maths by 8. Those who did not qualify English only were twice the number of students who did not qualify Maths only. Find the number of students who has qualified atleast two sections.
View Solution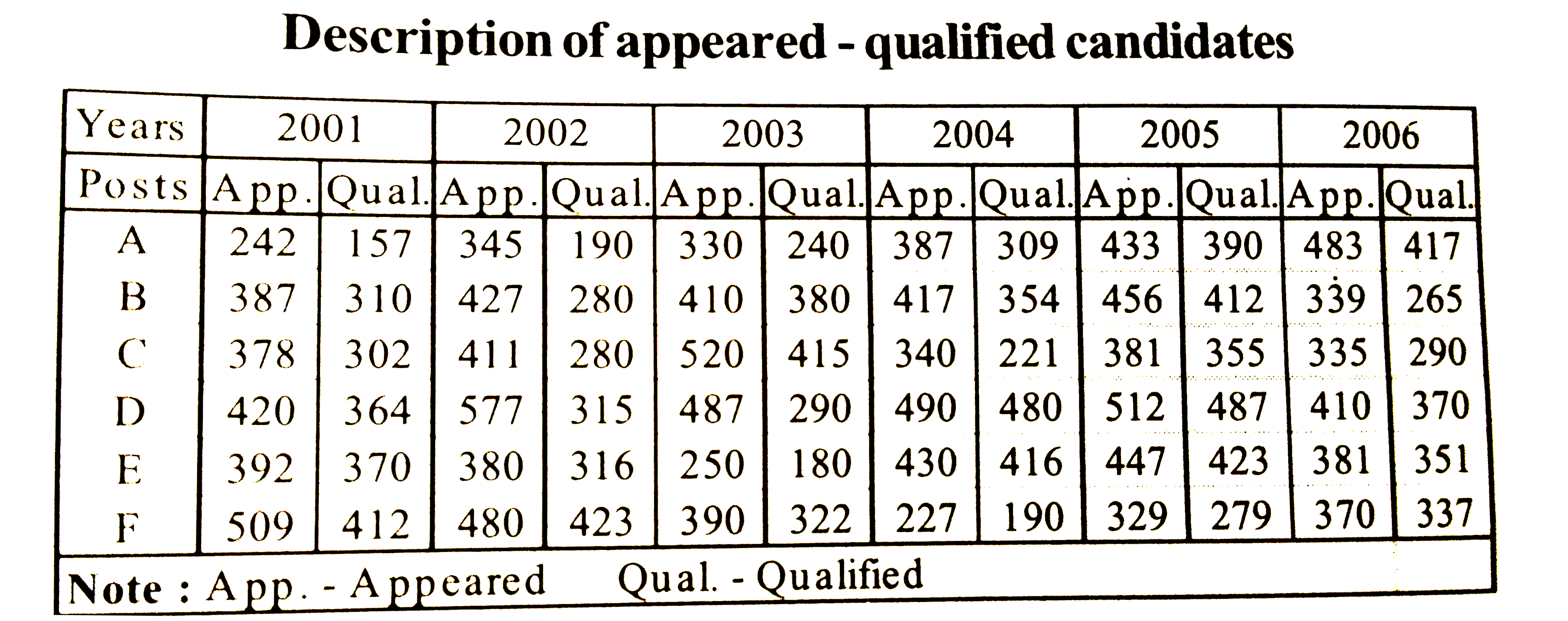
The average number of candidates who qualified for all the posts in the year 2004 is
View Solution
Knowledge Check
Find the number of aspirants who had qualified none of the section.
A12B18C7D0Number of aspirants who had qualified only in DI section
A17B22C27Dnone of theseIn this question, sentence is given with blank to be filled in with an appropriate word. Four alternatives are suggested for question. Choose the correct alternative out of the four.
He did not qualify ___ the job.AforBtoCagainstDwith
None of these two students can pass their qualifying test.
View SolutionFind the number of aspirants who had qualified in atleast two sections out of 4 sections.
View SolutionNumber of aspirants who had qualified in only Maths and LR sections:
View SolutionIn a class of 50 students ,each student passed Maths of English ,If 10 students passed Maths ,then find the number of students who passed English
View SolutionIn a class of 80 students 25 passed in QA and DI , 25 passed in DI and English , 20 passed in QA and English 10 student passed in all the there subjects .
If no students failed in all three subject , what is the total number of students who passed in QA only , DI only and English only ?
View Solution