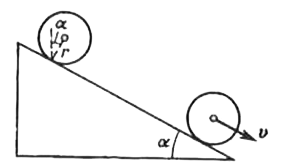
A solid cylinder with base radius jis placed on top of an inclined plane of length land slope angle α (Fig). The cylinder rolls down without slipping. Find the speed of the centre of mass of the cylinder at the bottom of the plane, if the coefficient of rolling friction is k. Can rolling friction be neglected? Do the calculation for the following conditions: l=1m,α=30∘,r=10cm,k=5×10−4m . What would be the speed if, in the absence of friction, the cylinder slides down?
The correct Answer is:2.7m/s;3.4m/s
From the law of conservation of energy
U−Mtr=K, or mg(lsinα+rcosα)−Troll=mv22+Iω22
The force of rolling friction is Trol=kmgcosα/r , the moment of inertia of a solid cylinder is I=1/2mr2 , and the angular velocity is ω=v/r . We have
mg(lsinα+rcosα)−lkmgcosαr=mv22+mv24
from which
v=√4g2(lsinα+rcosα−lkcosαr)
In principle the friction may not be neglected since in the absence of friction the disk will not roll down, but will slide down, and in this cage the kinetic energy of rolling should not be taken into account. But if the friction is small enough, the work of the force of friction may be neglected. The necessary condition for this is
lkr<<ltanα+r
For the numerical example contained in the problem we have
lkr=1×5×10−410−1=5×10−3,ltanα+r√33+0.1=0.68
i.e. the work of the force of rolling friction may be neglected in the calculation
When the cylinder slides down
mg(lsinα+rcosα)=12mv2,v=√2g(lsinα+rcosα)
Similar Questions
A cylinder of radius R and mass M rolls without slipping down a plane inclined at an angle θ. Coeff. of friction between the cylinder and the plane is μ. For what maximum inclination θ, the cylinder rolls without slipping ?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its centre of mass when the cylinder reaches its bottom ?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its center of mass when the cylinder reaches its bottom
View SolutionA solid cylinder of mass 'm' rolls without slipping down an inclined plane making an angle θ with the horizontal. The frictional force between the cylinder and the incline is
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination 45° then the minimum coefficient of friction required to support pure rolling is
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination 45°, then the minimum coefficient of friction required to support pure rolling is
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane without slipping. THE speed of its centre of mass when it reaches the bottom is
View Solution

