In a triangle ABC, ∠B=90∘,AB=8cm,BC=6cm. BD is perpendicular to AC, then find the length of CD, AD and BD.
The correct Answer is:CD=3.6,AD=6.4,BD=4.8
To solve the problem step by step, we will follow the approach outlined in the video transcript:
Step 1: Identify the triangle and given values
We have a right triangle ABC where:
- Angle B = 90°
- AB = 8 cm
- BC = 6 cm
Step 2: Find the length of AC using the Pythagorean theorem
According to the Pythagorean theorem:
AC2=AB2+BC2
Substituting the known values:
AC2=82+62
AC2=64+36
AC2=100
Now, taking the square root:
AC=√100=10 cm
Step 3: Find the length of CD using the similarity of triangles
Using the property of similar triangles, we can find CD:
CD=BC2AC
Substituting the known values:
CD=6210
CD=3610=3.6 cm
Step 4: Find the length of AD using the similarity of triangles
Similarly, we can find AD:
AD=AB2AC
Substituting the known values:
AD=8210
AD=6410=6.4 cm
Step 5: Find the length of BD using the formula for the area of the triangle
The length of BD can be found using the formula:
BD=AB×BCAC
Substituting the known values:
BD=8×610
BD=4810=4.8 cm
Summary of Results
- CD = 3.6 cm
- AD = 6.4 cm
- BD = 4.8 cm
We have a right triangle ABC where:
- Angle B = 90°
- AB = 8 cm
- BC = 6 cm
According to the Pythagorean theorem:
AC2=AB2+BC2
AC2=82+62
AC2=64+36
AC2=100
AC=√100=10 cm
Using the property of similar triangles, we can find CD:
CD=BC2AC
CD=6210
CD=3610=3.6 cm
Similarly, we can find AD:
AD=AB2AC
AD=8210
AD=6410=6.4 cm
The length of BD can be found using the formula:
BD=AB×BCAC
BD=8×610
BD=4810=4.8 cm
- CD = 3.6 cm
- AD = 6.4 cm
- BD = 4.8 cm
Topper's Solved these Questions
Similar Questions
If sides of triangle are (8,b,14) then
View SolutionThe LCM of two numbers is 864 and their HCF is 144.If one of the number is 288,the other number is:
View SolutionIn the given figure, ∠ABC=90∘andBD⊥AC. If BD=8cm,AD=4cm find CD.
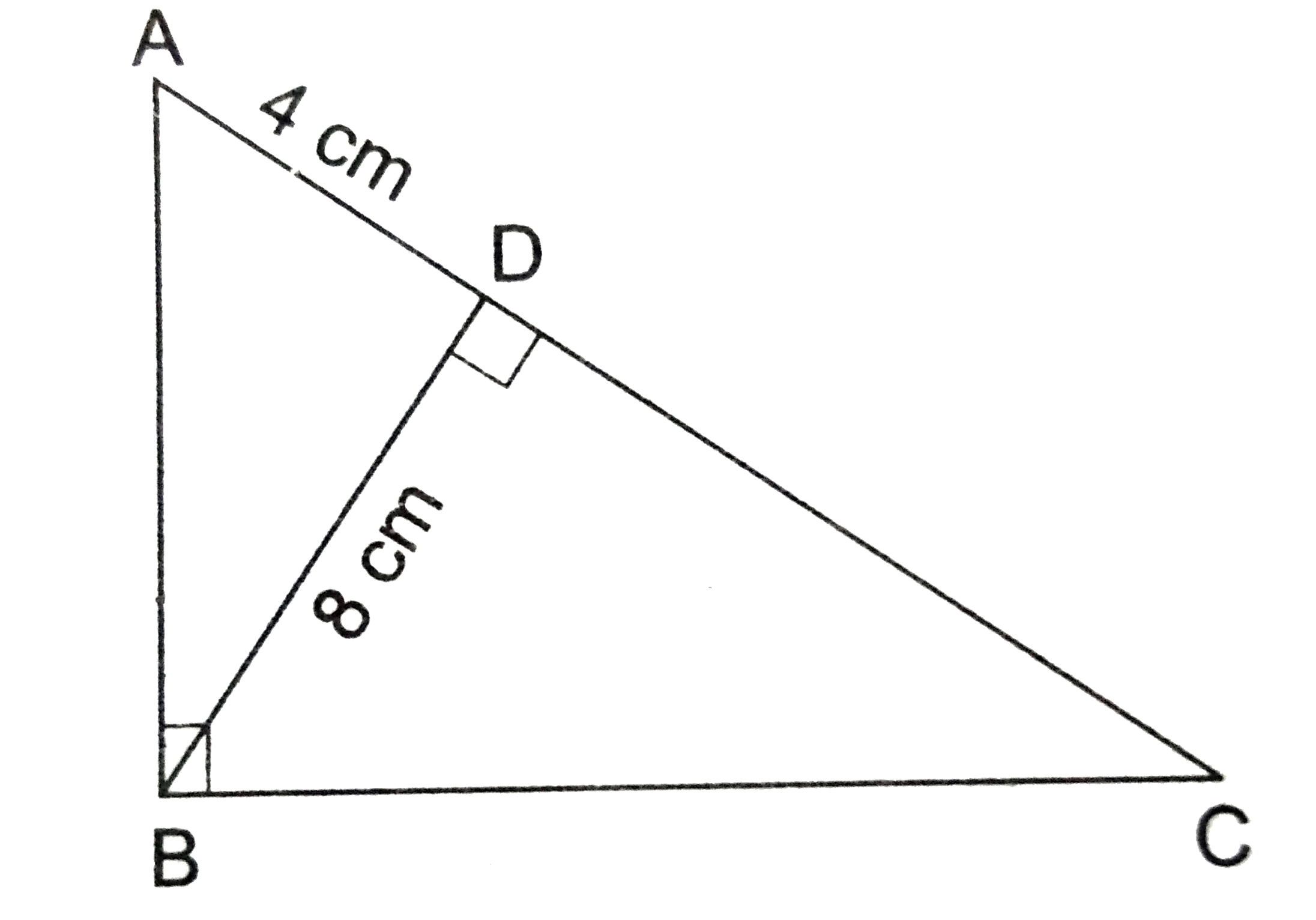
View SolutionΔABC is a right angled triangle where ∠B=90∘ and BD⊥AC . If BD = 8 cm , AD = 4 cm , then CD is ………..
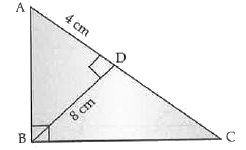
View SolutionIn ΔABC, ∠ABC=90∘, BD⊥AC. If BD=8cm, AD=4cm, find CD .
View SolutionIt the following figure, ∠ABC=90∘ and BD⊥AC. If AD=8cm, CD = 2 cm, then the length of BD is :

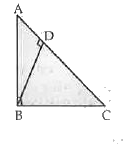
View SolutionIn ΔABC=90∘, BD⊥AC. If BD=8cm and AD=4cm, find CD.
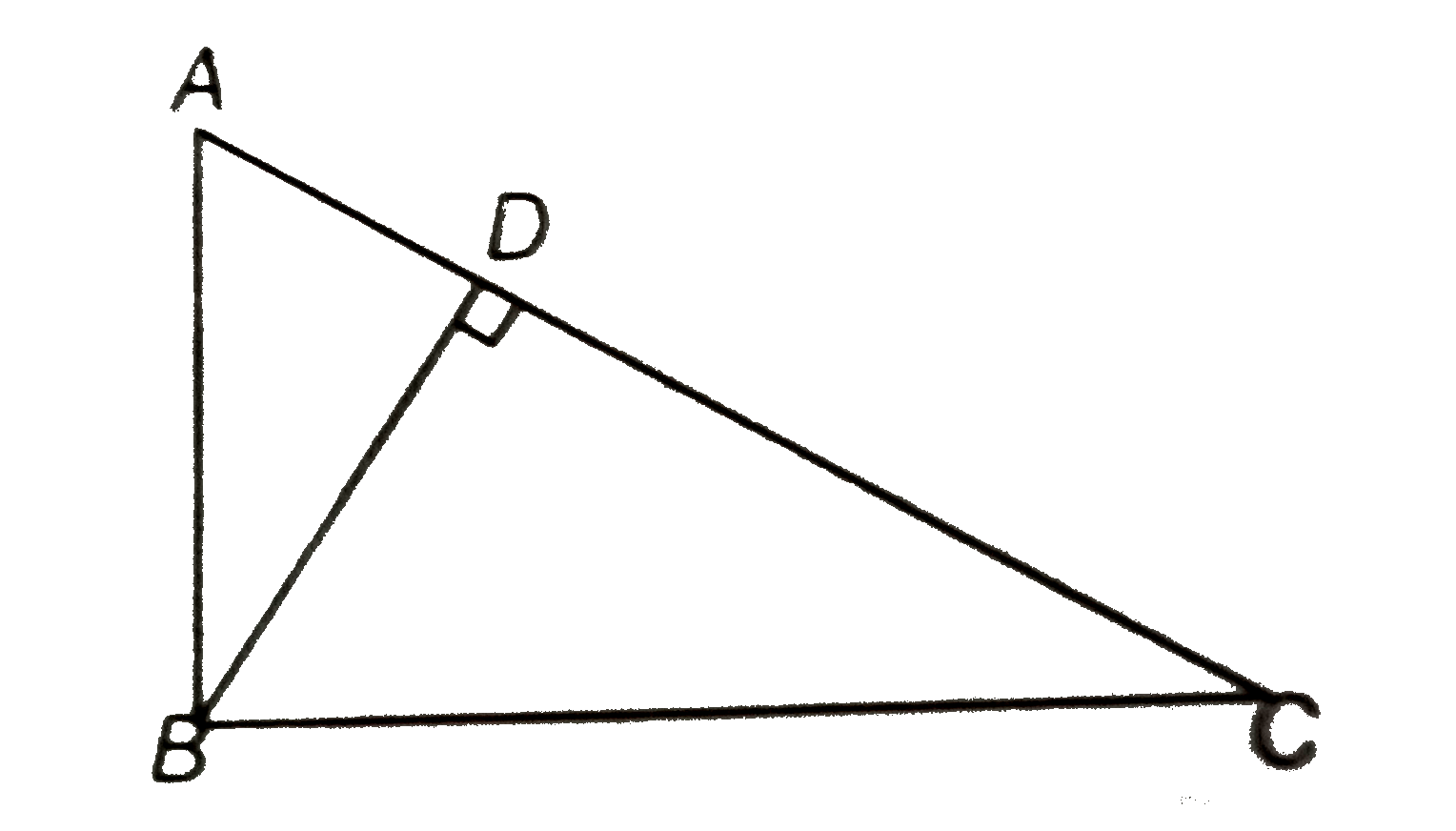
View SolutionIn given figure, ABC is a triangle right angled at B and BD⊥AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
View SolutionIn
 ABC, ∠ABC=90∘,BD⊥AC. If BD = 8 cm , AD = 4 cm, find CD and AB.
ABC, ∠ABC=90∘,BD⊥AC. If BD = 8 cm , AD = 4 cm, find CD and AB.
View Solutionत्रिभुज ABC में ∠B=90∘,AB=8 सेमी, BC=6 सेमी तथा BD, AC पर लम्ब है तो CD, AD व BD की लम्बाई ज्ञात कीजिये।
View SolutionIn a ΔABC,AB=5cm,AC=7cm,BC=6cm, If AD⊥BC BC. Find the length of BD.
View SolutionΔABC is a right angle triangle (right angled at B), BD is perpendicular to AC. If AC=16cmBC=9cm, find the length of CD.
View SolutionIn ΔABC,∠B=90∘ and BD⊥AC.
If CD = 10 cm and BD = 8 cm, find AD.
View SolutionIn △ABC,∠ABC=90∘ and BD bot Ac, if AB = 5 cm, BC = 12 cm, then find the length of BD.
View SolutionIn a right angled triangle ∠ABC=90 and BD⊥AC. If BD = 88 cm and AD = 4cm then find the length of CD.
View Solution
