The base BC of triangle ABC is divided at D so that BD = 12 DC.
Prove that area of ΔABD=13 of the area of ΔABC.
To prove that the area of triangle ΔABD is 13 of the area of triangle ΔABC, let's follow these steps:
Step 1: Understand the triangle and the point D
We have triangle ABC with base BC. Point D divides BC such that BD=12DC. This means that if we let DC=x, then BD=12x and thus BC=BD+DC=12x+x=32x.
Hint: Identify the relationships between the segments created by point D on base BC.
Step 2: Express the lengths in terms of a single variable
Let DC=x. Then, BD=12x and BC=32x.
Hint: Use a variable to simplify calculations and make relationships clearer.
Step 3: Draw the median AM
Draw the median AM from vertex A to the midpoint M of segment DC. Since M is the midpoint, we have DM=12DC=12x and CM=12DC=12x.
Hint: The median divides the triangle into two smaller triangles of equal area.
Step 4: Establish equal areas
Since AM is a median, it divides triangle ADC into two triangles ΔADM and ΔACM of equal area. Therefore, we can say:
Area of ΔADM=Area of ΔACM
Let’s denote the area of triangle ABC as S. Then, the area of triangle ADC is 23S because ΔABD and ΔADC together make up triangle ABC.
Hint: Use the property of medians to relate the areas of the triangles.
Step 5: Relate areas of triangles
Since BD=DM, triangle ABD is similar to triangle ADM. Therefore, the area of triangle ABD is equal to the area of triangle ADM:
Area of ΔABD=Area of ΔADM
Step 6: Calculate the area of triangle ABD
From the previous steps, we know:
Area of ΔABD=Area of ΔADM=12Area of ΔADC
Since the area of triangle ADC is 23S, we have:
Area of ΔABD=12⋅23S=13S
Conclusion
Thus, we have shown that the area of triangle ΔABD is 13 of the area of triangle ΔABC:
Area of ΔABD=13Area of ΔABC
Hint: Summarize the relationships and calculations to reinforce the conclusion.
We have triangle ABC with base BC. Point D divides BC such that BD=12DC. This means that if we let DC=x, then BD=12x and thus BC=BD+DC=12x+x=32x.
Let DC=x. Then, BD=12x and BC=32x.
Draw the median AM from vertex A to the midpoint M of segment DC. Since M is the midpoint, we have DM=12DC=12x and CM=12DC=12x.
Since AM is a median, it divides triangle ADC into two triangles ΔADM and ΔACM of equal area. Therefore, we can say:
Area of ΔADM=Area of ΔACM
Since BD=DM, triangle ABD is similar to triangle ADM. Therefore, the area of triangle ABD is equal to the area of triangle ADM:
Area of ΔABD=Area of ΔADM
From the previous steps, we know:
Area of ΔABD=Area of ΔADM=12Area of ΔADC
Area of ΔABD=12⋅23S=13S
Thus, we have shown that the area of triangle ΔABD is 13 of the area of triangle ΔABC:
Area of ΔABD=13Area of ΔABC
Topper's Solved these Questions
- AREA THEOREMSBook:ICSEChapter:AREA THEOREMSExercise:Exercies 16(C )
Explore 22 Videos
- AREA THEOREMSBook:ICSEChapter:AREA THEOREMSExercise:Exercies 16(A)
Explore 36 Videos
- AREA AND PERIMETER OF PLANE FIGURESBook:ICSEChapter:AREA AND PERIMETER OF PLANE FIGURESExercise:EXERCISE 20(D)
Explore 12 Videos
- CHAPTER REVISION (STAGE 2) Book:ICSEChapter:CHAPTER REVISION (STAGE 2) Exercise:DISTANCE FORMULA
Explore 12 Videos
Similar Questions
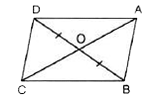
In the given figure, the diagonals AC and BD intersects at point O. If OB=OD and AB//DC, prove that :
(i) Area(ΔDOC)=Area(ΔAOB).
(ii) Area(ΔDCB)=Area(ΔACB).
(iii) ABCD is a parallelogram.
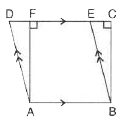
View SolutionIn the given figure, if area of triangle ADE is 60cm∘, giving reason, the area of :
(i) parallelogram ABED,
(ii) rectangle ABCF,
(iii) triangle ABE.
View SolutionThe perimeter of a triangle is 450 m and its sides are in the ratio 12:5:13. Find the area of the triangle.
View SolutionFind the distance between the origin and the point :
(-5, 12)
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionThe base BC of Delta ABC is divided at D, so that BD=(1)/(2)DC. Prove that ar(Delta ABD)=(1)/(3)ar(Delta ABC)
View SolutionIncircle of radius 4 of a triangle ABC touches the side BC at D .If BD=6cm,DC=8cm and Delta be the area of triangle then (Delta-3)^((1)/(4))
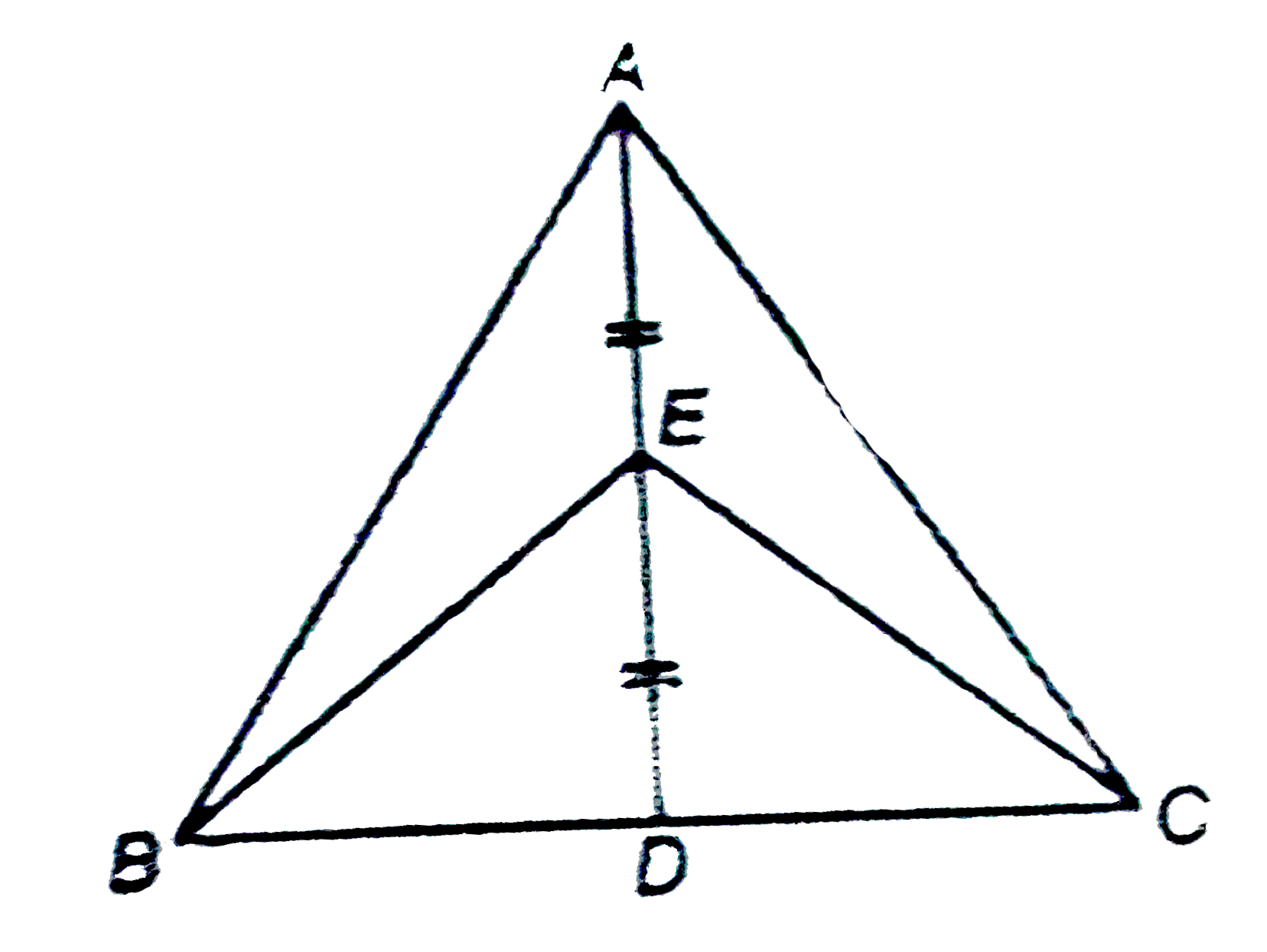
View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
View Solutionसिद्ध कीजिए कि किसी त्रिभुज की माध्यिका इसे दो समान क्षेत्रफल वाले त्रिभुजों में विभक्त करती है।
ज्ञात है: ΔABC जिसकी माध्यिका AD है।
सिद्ध करना है : "क्षे." (ΔABD)="क्षे." (ΔADC)
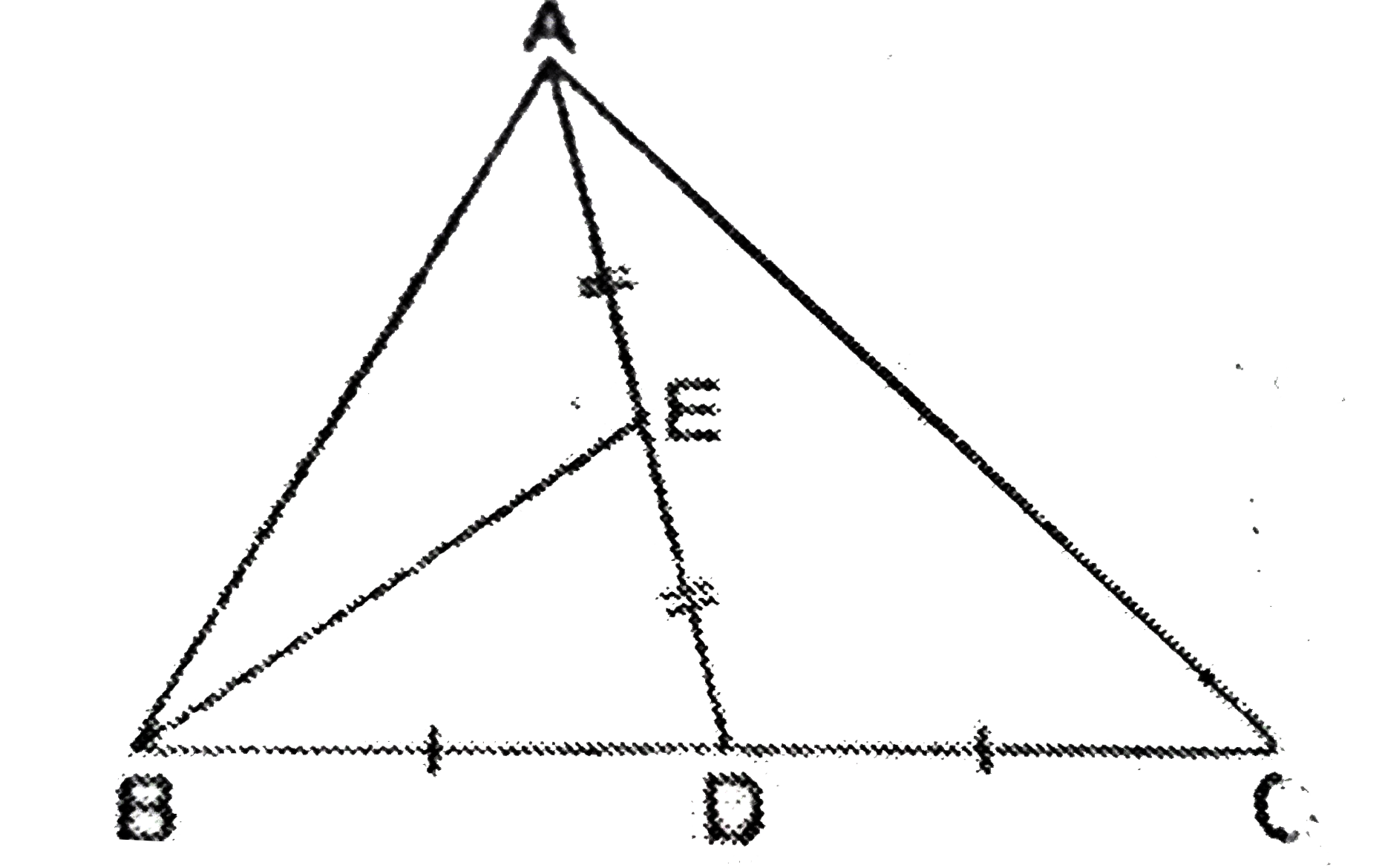
View Solutionएक त्रिभुज ABC में, BC का मध्य बिन्दु D है और AD का मध्य बिन्दु E है। सिद्ध कीजिए :
क्षेत्रफल (ΔBED)=14 क्षेत्रफल (ΔABC).
View Solutionयदि त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार दिया गया है कि BD = 2DC , तो सिद्ध कीजिए कि ar(ΔABD)=2ar(ΔADC)
View SolutionIn ΔABC,point D is on side BC such that DC = 6, BC = 15. find
(i)A(ΔABD):A(ΔABC) and
(ii) A(ΔABD):A(ΔADC).
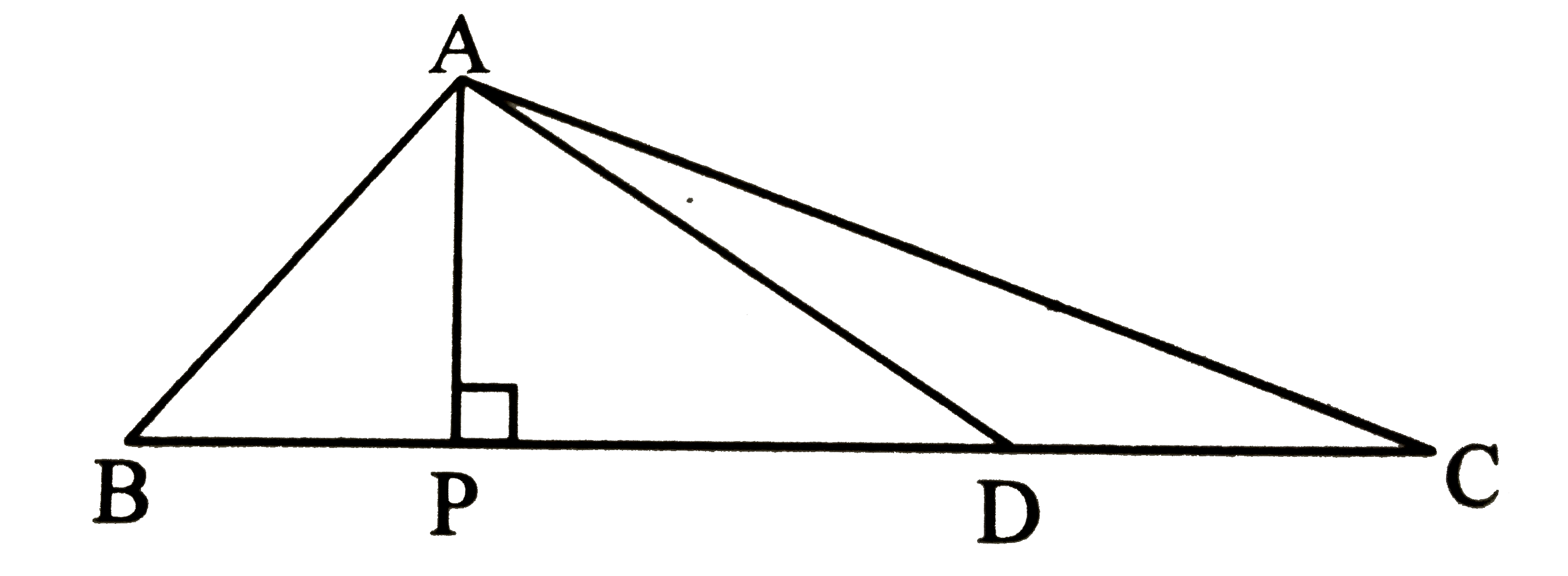
View SolutionΔABC का आधार BC बिन्दु D से इस प्रकार विभाजित होता है कि BD=12DC है। सिद्ध कीजिए कि ar(ΔABD)=13ar(ΔABC).
View Solutionचित्र में यदि AD⊥BC और BDDA=DADC हो, तो सिद्ध करो की ΔABC एक समकोण त्रिभुज है|
View SolutionBD = 1/3 BC ಆಗುವಂತೆ ಸಮಬಾಹು ತ್ರಿಭುಜ ABC ಯಲ್ಲಿ D ಯು BCಯ ಮೇಲಿನ ಒಂದು ಬಿಂದುವಾಗಿದೆ. 9AD2=7AB2ಎಂದು ಸಾಧಿಸಿ.
View Solution