The focus at (1,1) the directrix x−y=3.
The correct Answer is:x2+2xy+y2+2x−10y−5=0
To find the equation of the parabola with focus at (1, 1) and directrix given by the line x−y=3, we can follow these steps:
Step 1: Understand the Definition of a Parabola
A parabola is defined as the set of all points P such that the distance from P to the focus F is equal to the distance from P to the directrix D.
Step 2: Set Up the Problem
Let P(x,y) be a point on the parabola. The focus F is at (1,1) and the directrix is given by the equation x−y=3. We can rewrite the directrix in the standard form:
x−y−3=0
Step 3: Calculate the Distance from Point P to the Focus F
The distance PF from point P(x,y) to the focus F(1,1) is given by the distance formula:
PF=√(x−1)2+(y−1)2
Step 4: Calculate the Distance from Point P to the Directrix
The distance PM from point P(x,y) to the directrix can be calculated using the formula for the distance from a point to a line Ax+By+C=0:
PM=|Ax1+By1+C|√A2+B2
Here, A=1, B=−1, and C=−3. Thus,
PM=|1⋅x−1⋅y−3|√12+(−1)2=|x−y−3|√2
Step 5: Set the Distances Equal
According to the definition of the parabola, we have:
PF=PM
Substituting the distances we found:
√(x−1)2+(y−1)2=|x−y−3|√2
Step 6: Square Both Sides
Squaring both sides to eliminate the square root gives:
(x−1)2+(y−1)2=(x−y−3)22
Step 7: Multiply Through by 2
To eliminate the fraction, multiply both sides by 2:
2((x−1)2+(y−1)2)=(x−y−3)2
Step 8: Expand Both Sides
Expanding the left side:
2((x2−2x+1)+(y2−2y+1))=2x2+2y2−4x−4y+4
Expanding the right side:
(x−y−3)2=x2−2xy+y2+9−6x+6y
Step 9: Set the Expanded Forms Equal
Now we have:
2x2+2y2−4x−4y+4=x2−2xy+y2+9−6x+6y
Step 10: Rearrange the Equation
Rearranging gives:
2x2+2y2−x2−y2+2xy+2x−10y−5=0
This simplifies to:
x2+y2+2xy+2x−10y−5=0
Final Equation
Thus, the equation of the parabola is:
x2+y2+2xy+2x−10y−5=0
A parabola is defined as the set of all points P such that the distance from P to the focus F is equal to the distance from P to the directrix D.
Let P(x,y) be a point on the parabola. The focus F is at (1,1) and the directrix is given by the equation x−y=3. We can rewrite the directrix in the standard form:
x−y−3=0
The distance PF from point P(x,y) to the focus F(1,1) is given by the distance formula:
PF=√(x−1)2+(y−1)2
The distance PM from point P(x,y) to the directrix can be calculated using the formula for the distance from a point to a line Ax+By+C=0:
PM=|Ax1+By1+C|√A2+B2
Here, A=1, B=−1, and C=−3. Thus,
PM=|1⋅x−1⋅y−3|√12+(−1)2=|x−y−3|√2
According to the definition of the parabola, we have:
PF=PM
Substituting the distances we found:
√(x−1)2+(y−1)2=|x−y−3|√2
Squaring both sides to eliminate the square root gives:
(x−1)2+(y−1)2=(x−y−3)22
To eliminate the fraction, multiply both sides by 2:
2((x−1)2+(y−1)2)=(x−y−3)2
Expanding the left side:
2((x2−2x+1)+(y2−2y+1))=2x2+2y2−4x−4y+4
Expanding the right side:
(x−y−3)2=x2−2xy+y2+9−6x+6y
Now we have:
2x2+2y2−4x−4y+4=x2−2xy+y2+9−6x+6y
Rearranging gives:
2x2+2y2−x2−y2+2xy+2x−10y−5=0
This simplifies to:
x2+y2+2xy+2x−10y−5=0
Thus, the equation of the parabola is:
x2+y2+2xy+2x−10y−5=0
Topper's Solved these Questions
- PARABOLABOOK - ICSECHAPTER - PARABOLAEXERCISE - CHAPTER TEST
8 Videos
- PARABOLABOOK - ICSECHAPTER - PARABOLAEXERCISE - TRY THESE
3 Videos
- MOVING AVERAGEBOOK - ICSECHAPTER - MOVING AVERAGEEXERCISE - CHAPTER TEST
5 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - ICSECHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - MULTIPLE CHOICE QUESTIONS
32 Videos
Similar Questions
The equation of the diirectrix of the parabola is 3x+2y+1−0. The focus is (2,1). Find the equation of the parabola.
View SolutionFind the equation of the parabola whose
vertex is at the point (−2,2) and whose focus is (−6,−6).
View SolutionThe following table gives the numbers of failures of commercial industries in a country during the years 1975 to 1990.
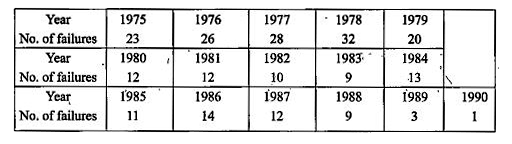
Draw the graph illustrating the figures.
calculate the 4-yearly moveing average and plot them on the same graph.
View SolutionThe number of 3 digit odd number, when repetition of digits is allowed is
View SolutionFInd the equation of the parabola The focus at (1,1) the directrix x-y=3
View SolutionFind the equation of the ellipse whose eccentricity is 1/2, the focus is (1,1) and the directrix is x−y+3=0.
View SolutionThe equation of the directrix of a hyperbola is x−y+3=0. Its focus is (-1,1) and eccentricity 3. Find the equation of the hyperbola.
View SolutionThe equation of the parabola whose focus is (1,1) and the directrix is x+y+1=0
View SolutionThe equation of the directrix of a hyperbola is x-y+3 = 0. Its focus is (-1,1) and eccentricity is 2 . Find the equation of the hyperbola.
View SolutionFind the equation of the hyperbola whose
eccentricity is 3, focus is (-1,1) and equation of directrix is x - y + 3 = 0.
View SolutionThe equation of the directrix of a hyperbola x - y + 3 = 0 . One of its focus is at (-1,1) and eccentricity is 3 . Find the equation of the hyperbola .
View SolutionThe equation of an ellipse whose focus is (−1,1), directrix is x−y+3=0 and eccentricity is 12, is given by
View SolutionFind the equation of the ellipse whose
eccentricity is 12 , focus is (-1,1) , directrix is x - y + 3 = 0 .
View SolutionThe equation of the ellipse with focus (-1,1) directrix x−y+3=0 and eccentricity 12 is
View SolutionIf for a conic section a focus is (-1,1), eccentricity=3 and the equation of the corresponding directrix is x-y+3=0, then the equation of this conic section is
View SolutionFind the equation of the ellipse with focus at (−1,1) and eccentricity 12 and directrix x−y+3=0.
View Solution

