In sub-parts (i) and (ii) choose the correct option and in sub-parts (iii) to (v), answer the questions as instructed.
Find the area of triangle whose two adjacent sides are given by →a=ˆi+4ˆj−ˆk and →b=ˆi+ˆj+2ˆk
The correct Answer is:32√11≈4.97 sq . Units
To find the area of the triangle formed by two adjacent sides represented by the vectors →a=^i+4^j−^k and →b=^i+^j+2^k, we can follow these steps:
Step 1: Calculate the Cross Product →a×→b
The area of the triangle can be calculated using the formula:
Area=12∥→a×→b∥
First, we need to calculate the cross product →a×→b.
→a=⎛⎜⎝14−1⎞⎟⎠,→b=⎛⎜⎝112⎞⎟⎠
The cross product can be calculated using the determinant:
→a×→b=∣∣
∣
∣∣^i^j^k14−1112∣∣
∣
∣∣
Step 2: Calculate the Determinant
Calculating the determinant:
→a×→b=^i∣∣∣4−112∣∣∣−^j∣∣∣1−112∣∣∣+^k∣∣∣1411∣∣∣
Calculating each of the 2x2 determinants:
1. ∣∣∣4−112∣∣∣=(4)(2)−(−1)(1)=8+1=9
2. ∣∣∣1−112∣∣∣=(1)(2)−(−1)(1)=2+1=3
3. ∣∣∣1411∣∣∣=(1)(1)−(4)(1)=1−4=−3
Putting it all together:
→a×→b=9^i−3^j−3^k
Step 3: Calculate the Magnitude of the Cross Product
Now, we find the magnitude of →a×→b:
∥→a×→b∥=√92+(−3)2+(−3)2=√81+9+9=√99
Step 4: Calculate the Area of the Triangle
Now we can calculate the area of the triangle:
Area=12∥→a×→b∥=12√99
Final Step: Simplify the Area
We can simplify √99 as follows:
√99=√9×11=3√11
Thus, the area becomes:
Area=12×3√11=32√11
Conclusion
The area of the triangle is:
Area=32√11(approximately 4.97 square units)
Area=12∥→a×→b∥
First, we need to calculate the cross product →a×→b.
→a×→b=∣∣
∣
∣∣^i^j^k14−1112∣∣
∣
∣∣
→a×→b=^i∣∣∣4−112∣∣∣−^j∣∣∣1−112∣∣∣+^k∣∣∣1411∣∣∣
1. ∣∣∣4−112∣∣∣=(4)(2)−(−1)(1)=8+1=9
→a×→b=9^i−3^j−3^k
∥→a×→b∥=√92+(−3)2+(−3)2=√81+9+9=√99
Area=12∥→a×→b∥=12√99
√99=√9×11=3√11
Thus, the area becomes:
Area=12×3√11=32√11
Area=32√11(approximately 4.97 square units)
Topper's Solved these Questions
- MOCK TEST PAPER -2021 Book:ICSEChapter:MOCK TEST PAPER -2021 Exercise:SECTION -C (15 MARKS )
Explore 10 Videos
- MOCK TEST PAPER -2021 Book:ICSEChapter:MOCK TEST PAPER -2021 Exercise:SECTION -C (15 MARKS )
Explore 10 Videos
- MATRICESBook:ICSEChapter:MATRICESExercise:MULTIPLE CHOICE QUESTION (Competency based questions)
Explore 25 Videos
- MODEL TEST PAPER - 10Book:ICSEChapter:MODEL TEST PAPER - 10Exercise:SECTION - C
Explore 10 Videos
Similar Questions
If the regression coefficients y on x and x on y respectively are 0.8 and 0.2, what would be the value of coefficient of correlation?
View SolutionIf the regression coefficients y on x and x on y respectively are 0.8 and 0.2, what would be the value of coefficient of correlation?
View SolutionA firm produces three products P1P2 and P3 requiring the mix-up of three materials M1,M2 and M3 per unit requirement of each product for each material (in units) is represented by matrix A as follows:
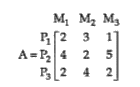
The per unit cost of material M1,M2 and M3 is 5, 10 and 15 respectively.
If C represents the matrix showing cost of material, the matrix C will be expressed as :
View SolutionThe angle between the regression lines: x−2y+3=0,4x−5y+1=0 is
View Solutionउस समांतर चतुर्भुज का क्षेत्रफ़ल ज्ञात कीजिए जिसकी संलग्न भुजाये →a=3ˆi+ˆj+4ˆk और →b=ˆi−ˆj+ˆk द्वारा दी गयी है!
View Solutionउस समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी संलग्न भुजाएं →a=3ˆi+ˆj+4ˆk और →b=ˆi−ˆj+ˆk द्वारा दी गई है।
View Solutionउस समांतर चतुर्भुज का क्षेत्रफल ज्ञात किजिए जिसकी संलग्न भुजाए →a=3ˆi+ˆj+4ˆk और →b=ˆi−ˆj+ˆk द्वारा दी गयी है ।
View SolutionFind the area of the parallelogram whose adjacent sides are given by the vectors →a=ˆi−ˆj+3ˆkand→b=2ˆi−7ˆj+ˆk
View SolutionFind the area of parallelogram whose adjacent sides are given by the vectors : →a=3ˆi+ˆj+4ˆk and →b=ˆi−ˆj+ˆk.
View SolutionFind the area of parallelogram whose adjacent sides are given by the vectors : →a=2ˆi−ˆj+3ˆk and →b=ˆi+ˆj−2ˆk.
View SolutionFind the area of parallelogram whose adjacent sides are given by the vectors : →a=ˆi+ˆj−ˆk and →b=2ˆi−ˆj+3ˆk.
View SolutionFind the area of parallelogram whose adjacent sides are given by the vectors →a=ˆi−ˆj+3ˆk and →b=2ˆi−7ˆj+ˆk.
View SolutionIn sub - part (i) and (ii) choose the correct option and in sub - part (iii) to (v) answer the questions as instructed.
~q→~p is equivalent to ……
View SolutionFind the area of the parallelogram whose adjacent sides determined by vectors.
→a=ˆi+ˆj−ˆk →b=ˆi−ˆj+ˆk
View SolutionFind the area of a parallelogram whose adjacent sides are given by the vectors →a=3ˆi+ˆj+4ˆk and →b=ˆi−ˆj+ˆk
View Solution
