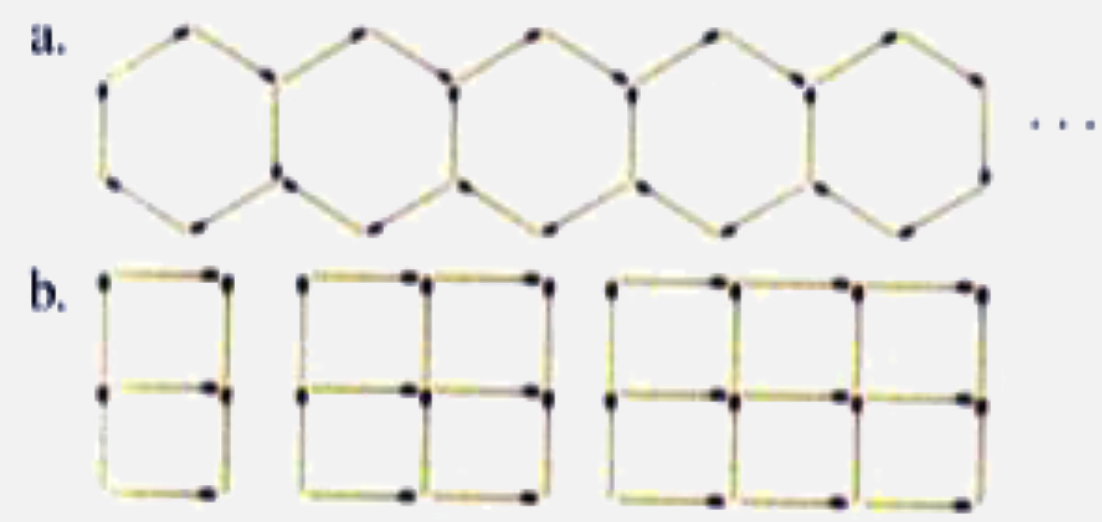
Look at the following matchstick pattern of squares. The squares are not separate. Two neighboring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint: If you remove the vertical stick at the end, you will get a pattern of Cs.)
To find the number of matchsticks in terms of the number of squares, we can analyze the pattern of matchsticks used to form the squares.
1. Identify the Matchsticks for One Square:
- A single square is formed by 4 matchsticks.
- Therefore, for 1 square, the number of matchsticks = 4.
2. Identify the Matchsticks for Two Squares:
- When we add a second square, it shares one matchstick with the first square.
- Thus, for 2 squares, the matchsticks used = 4 (for the first square) + 3 (for the second square) = 7.
3. Identify the Matchsticks for Three Squares:
- For three squares, the first square uses 4 matchsticks, the second square uses 3 matchsticks (shared), and the third square also uses 3 matchsticks (shared).
- Therefore, for 3 squares, the matchsticks used = 4 + 3 + 3 = 10.
4. Identify the Matchsticks for Four Squares:
- Continuing this pattern, for four squares, we have:
- 4 (for the first square) + 3 (for the second square) + 3 (for the third square) + 3 (for the fourth square) = 13 matchsticks.
5. Establish a General Rule:
- From the observations:
- 1 square = 4 matchsticks
- 2 squares = 7 matchsticks
- 3 squares = 10 matchsticks
- 4 squares = 13 matchsticks
- We can see that each additional square adds 3 matchsticks (since they share one matchstick with the previous square).
- Therefore, we can establish a formula:
- Number of matchsticks (M) = 3 * (number of squares (x)) + 1.
6. Write the General Formula:
- The general formula for the number of matchsticks in terms of the number of squares is:
M=3x+1
- Where x is the number of squares.
- A single square is formed by 4 matchsticks.
- Therefore, for 1 square, the number of matchsticks = 4.
- When we add a second square, it shares one matchstick with the first square.
- Thus, for 2 squares, the matchsticks used = 4 (for the first square) + 3 (for the second square) = 7.
- For three squares, the first square uses 4 matchsticks, the second square uses 3 matchsticks (shared), and the third square also uses 3 matchsticks (shared).
- Therefore, for 3 squares, the matchsticks used = 4 + 3 + 3 = 10.
- Continuing this pattern, for four squares, we have:
- 4 (for the first square) + 3 (for the second square) + 3 (for the third square) + 3 (for the fourth square) = 13 matchsticks.
- From the observations:
- 1 square = 4 matchsticks
- 2 squares = 7 matchsticks
- 3 squares = 10 matchsticks
- 4 squares = 13 matchsticks
- We can see that each additional square adds 3 matchsticks (since they share one matchstick with the previous square).
- Therefore, we can establish a formula:
- Number of matchsticks (M) = 3 * (number of squares (x)) + 1.
- The general formula for the number of matchsticks in terms of the number of squares is:
M=3x+1
- Where x is the number of squares.
Similar Questions
(a) Look at the following matchstick pattern of squares (Fig 11.6). The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint : If you remove the vertical stick at the end, you will get a pattern of Cs.)(b) Fig 11.7 gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.
View SolutionFigs. Below gives a matchstick pattern of triangles. Find the general rule that gives the number of matchsticks in terms of the number of triangles.
View SolutionWrite the rule that gives the number of matchsticks required to make a pattern of letter M.
View SolutionFind the rule which gives the number of matchsticks required to make a pattern of n such shapes.
View SolutionWrite the rule that gives the number of matchsticks required to make the following pattern.

View SolutionFind a rule which gives the number of matchsticks required to make a pattern of the letter E as E
View SolutionFind the rule that gives the number of matchsticks required to make the following pattern. Also, find the number of matchsticks required to make a pattern of 9 diamonds.

View SolutionFind a rule that gives the number of line segments required to make the following pattern of squares.

View SolutionFind the rule that gives the number of matchsticks required to build the following pattern. Also find the number of matchsticks required to make a pattern with 6 squares at the base.
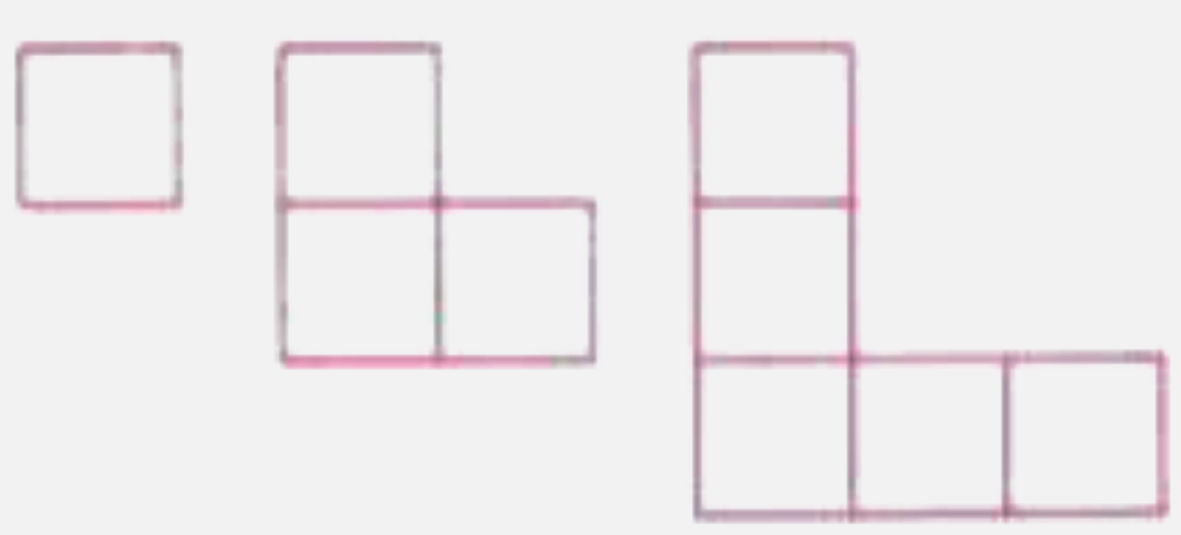
View SolutionFind a rule that gives the number of line segments required to make the following pattern.

View Solution
