The area of the sector of a circle with radius 6 cm and of angle 60∘ is
9.42cm2
37.68cm2
18.84cm2
19.84cm2
To find the area of the sector of a circle with a radius of 6 cm and an angle of 60 degrees, we can follow these steps:
1. Identify the given values:
- Radius (r) = 6 cm
- Angle (θ) = 60 degrees
2. Recall the formula for the area of a sector:
Area of the sector=θ360×πr2
3. Substitute the known values into the formula:
Area of the sector=60360×π×(6)2
4. Simplify the fraction:
60360=16
So the formula becomes:
Area of the sector=16×π×(6)2
5. Calculate (6)2:
(6)2=36
Now substitute this back into the formula:
Area of the sector=16×π×36
6. Multiply 16 by 36:
16×36=6
So now we have:
Area of the sector=6π
7. Use the approximate value of π (3.14):
Area of the sector≈6×3.14=18.84 cm2
8. Final Result:
The area of the sector is approximately 18.84 cm2.
- Radius (r) = 6 cm
- Angle (θ) = 60 degrees
Area of the sector=θ360×πr2
Area of the sector=60360×π×(6)2
60360=16
So the formula becomes:
Area of the sector=16×π×(6)2
(6)2=36
Now substitute this back into the formula:
Area of the sector=16×π×36
16×36=6
So now we have:
Area of the sector=6π
Area of the sector≈6×3.14=18.84 cm2
The area of the sector is approximately 18.84 cm2.
Topper's Solved these Questions
- AREA THEOREMSBook:ICSEChapter:AREA THEOREMSExercise:Exercies 16(A)
Explore 36 Videos
- AREA THEOREMSBook:ICSEChapter:AREA THEOREMSExercise:Exercies 16(B)
Explore 16 Videos
- AREA AND PERIMETER OF PLANE FIGURESBook:ICSEChapter:AREA AND PERIMETER OF PLANE FIGURESExercise:EXERCISE 20(D)
Explore 12 Videos
- CHAPTER REVISION (STAGE 2) Book:ICSEChapter:CHAPTER REVISION (STAGE 2) Exercise:DISTANCE FORMULA
Explore 12 Videos
Similar Questions
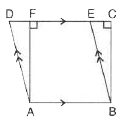
In the given figure, if area of triangle ADE is 60cm∘, giving reason, the area of :
(i) parallelogram ABED,
(ii) rectangle ABCF,
(iii) triangle ABE.
View SolutionShow that :
(i) a diagonal divides a parallelogram into two triangles of equal area.
(ii) the ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
(iii) the ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
View SolutionThe perimeter of a triangle is 450 m and its sides are in the ratio 12:5:13. Find the area of the triangle.
View SolutionFind the distance between the origin and the point :
(-5, 12)
View Solution6 cm त्रिज्या वाले एक वृत्त के एक त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए जिसका कोण 60∘ है।
View Solution6सेमी त्रिज्या वाले एक वृत के एक त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए जिसका कोण 60∘ है ।
View Solution6 सेमी त्रिज्या वाले एक वृत्त के एक त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए जिसका कोण 60∘ है।
View SolutionIf the radius of circle is 6 cm and the central angle is 280∘, then the area of the corrseponding sector is
View SolutionFind the area of a sector of a circle with radius 6 cm if angle of the sector is 60∘. use π=227
View SolutionArea of sector subtends angle 60∘ at centre of circle of radius 3 cm is
View Solution5 सेमी त्रिज्या वाले एक वृत्त के एक त्रिज्यखण्ड का क्षेत्रफल,जिसका कोण 60∘ हो:
View Solution14 सेमी त्रिज्या वाले वृत्त के त्रिज्यखंड का क्षेत्रफल होगा। जिसका कोण 60∘ हो:
View SolutionFind the area of sector of a circle with radius 6cm, if angle of the sector is 60∘
View SolutionFind the area of sector of a circle with radius 4 cm and angle 60∘.
View SolutionFind the area of the sector of a circle with radius 5 cm and angle 60∘.
View Solution