In the given figure, a square is inscribed in a circle with centre O. Find :
∠BOD .Is BD a diameter of the circle
To solve the problem, we need to find the angle ∠BOD and determine if BD is a diameter of the circle.
1. Understanding the Figure: We have a square inscribed in a circle with center O. The vertices of the square are labeled as A,B,C, and D.
2. Identifying the Diagonals: The diagonals of the square AC and BD intersect at the center O of the circle. By the properties of a square, the diagonals bisect each other at right angles.
3. Finding ∠COD: Since the diagonals of the square intersect at right angles, we have:
∠COD=90∘
4. Using the Straight Line Property: The line BD is a straight line, which means that the angles on a straight line sum up to 180∘. Therefore, we can write:
∠BOC+∠COD=180∘
5. Substituting the Known Angle: We know ∠COD=90∘. Thus, we can substitute this into the equation:
∠BOC+90∘=180∘
6. Solving for ∠BOC: Rearranging the equation gives us:
∠BOC=180∘−90∘=90∘
7. Finding ∠BOD: Since ∠BOD is the sum of ∠BOC and ∠COD:
∠BOD=∠BOC+∠COD=90∘+90∘=180∘
8. Conclusion about Diameter: Since ∠BOD=180∘, it confirms that BD is indeed a straight line passing through the center O, which means BD is a diameter of the circle.
Final Answer:
- ∠BOD=180∘
- Yes, BD is a diameter of the circle.
∠COD=90∘
∠BOC+∠COD=180∘
∠BOC+90∘=180∘
∠BOC=180∘−90∘=90∘
∠BOD=∠BOC+∠COD=90∘+90∘=180∘
- ∠BOD=180∘
- Yes, BD is a diameter of the circle.
Topper's Solved these Questions
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(B)
15 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
- CIRCLES BOOK - ICSECHAPTER - CIRCLES EXERCISE - TOPIC-2
25 Videos
Similar Questions
In the given figure, a square is inscribed in a circle with centre O. Find :
∠COD . Is BD a diameter of the circle
View SolutionIn the given figure, a square is inscribed in a circle with centre O. Find :
∠BOC . Is BD a diameter of the circle
View SolutionIn the given figure, a square is inscribed in a circle with centre O. Find :
∠OCB . Is BD a diameter of the circle
View SolutionIn the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
∠OBC
View SolutionIn the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
∠BOC
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
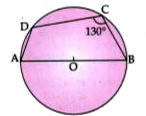
∠BCD=130∘. Find
(i) ∠DAB
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
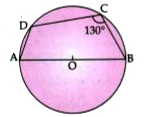
∠BCD=130∘. Find
(ii) ∠DBA
View SolutionA square is inscribed in a circle of radius 7 cm. Find the area of the square.
View SolutionIn figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle . Is the area of the outer square four times the area of the inner square ? Give reason for your answer.

View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
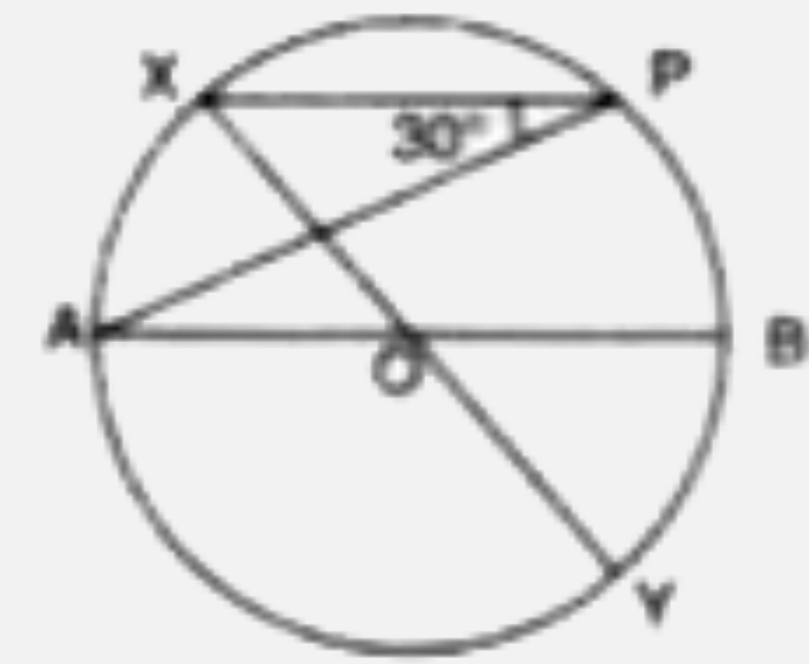
∠OAX
View Solution
