In the given figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC.
if ∠AOB=100∘ find ∠BOC
To solve the problem, we need to find the angle ∠BOC given that the length of arc AB is twice the length of arc BC and that ∠AOB=100∘.
1. Understanding the relationship between arcs and angles:
- The length of an arc in a circle is directly proportional to the angle subtended by that arc at the center of the circle. Therefore, if the length of arc AB is twice that of arc BC, the angle subtended by arc AB will also be twice that of arc BC.
2. Let the angle subtended by arc BC be x:
- Since the angle AOB=100∘, we can express the relationship as:
∠AOB=∠AB+∠BOC
- We know that ∠AB=2x (because the length of arc AB is twice that of arc BC).
3. Setting up the equation:
- The total angle at the center O is:
∠AOB+∠BOC=100∘+x
- Since ∠AOB=2x, we can write:
2x+x=100∘
- This simplifies to:
3x=100∘
4. Solving for x:
- Dividing both sides by 3 gives:
x=100∘3≈33.33∘
5. Finding ∠BOC:
- Since ∠BOC=x, we have:
∠BOC=100∘3≈33.33∘
Final Answer:
∠BOC≈33.33∘
- The length of an arc in a circle is directly proportional to the angle subtended by that arc at the center of the circle. Therefore, if the length of arc AB is twice that of arc BC, the angle subtended by arc AB will also be twice that of arc BC.
- Since the angle AOB=100∘, we can express the relationship as:
∠AOB=∠AB+∠BOC
- We know that ∠AB=2x (because the length of arc AB is twice that of arc BC).
- The total angle at the center O is:
∠AOB+∠BOC=100∘+x
- Since ∠AOB=2x, we can write:
2x+x=100∘
- This simplifies to:
3x=100∘
- Dividing both sides by 3 gives:
x=100∘3≈33.33∘
- Since ∠BOC=x, we have:
∠BOC=100∘3≈33.33∘
∠BOC≈33.33∘
टॉपर्स ने हल किए ये सवाल
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(B)
15 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
- CIRCLES BOOK - ICSECHAPTER - CIRCLES EXERCISE - TOPIC-2
25 Videos
समान प्रश्न
The radius of a circle is 13 cm and the length of one of its chords is 24 cm. Find the distance of the chord from the centres.
View SolutionThe figure shows two concentric circles and AD is a chord of larger circle.
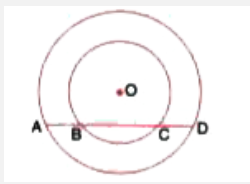
Prove that : AB = CD.
View SolutionFind distance between the points A (a,b) and B( - b,a)
View SolutionIn the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
∠BOC
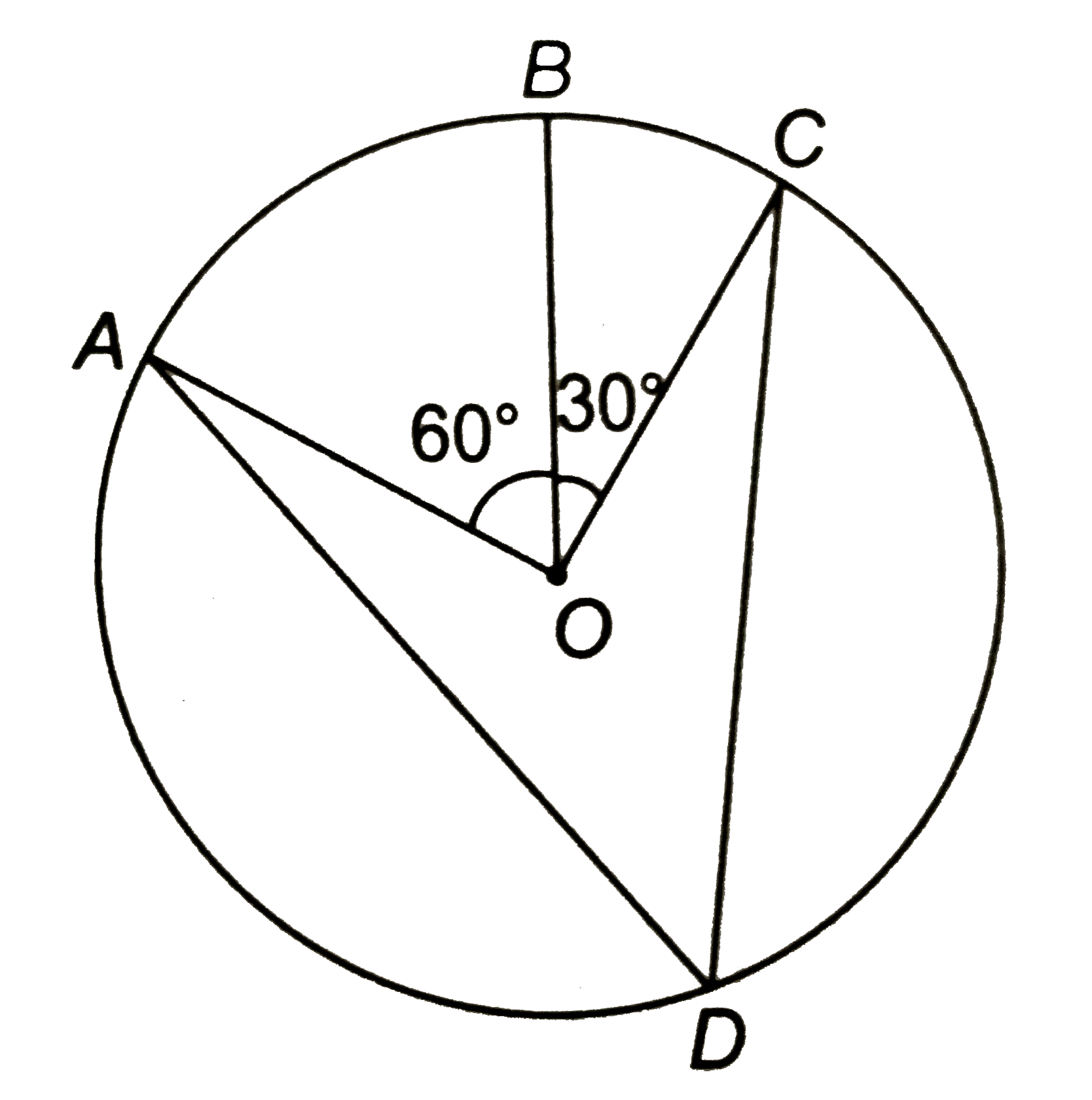
View Solutionआकृति में, केन्द्र O वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC=30∘ तथा ∠AOB=60∘ है | यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिन्दु है, तो ∠ADC ज्ञात कीजिए |
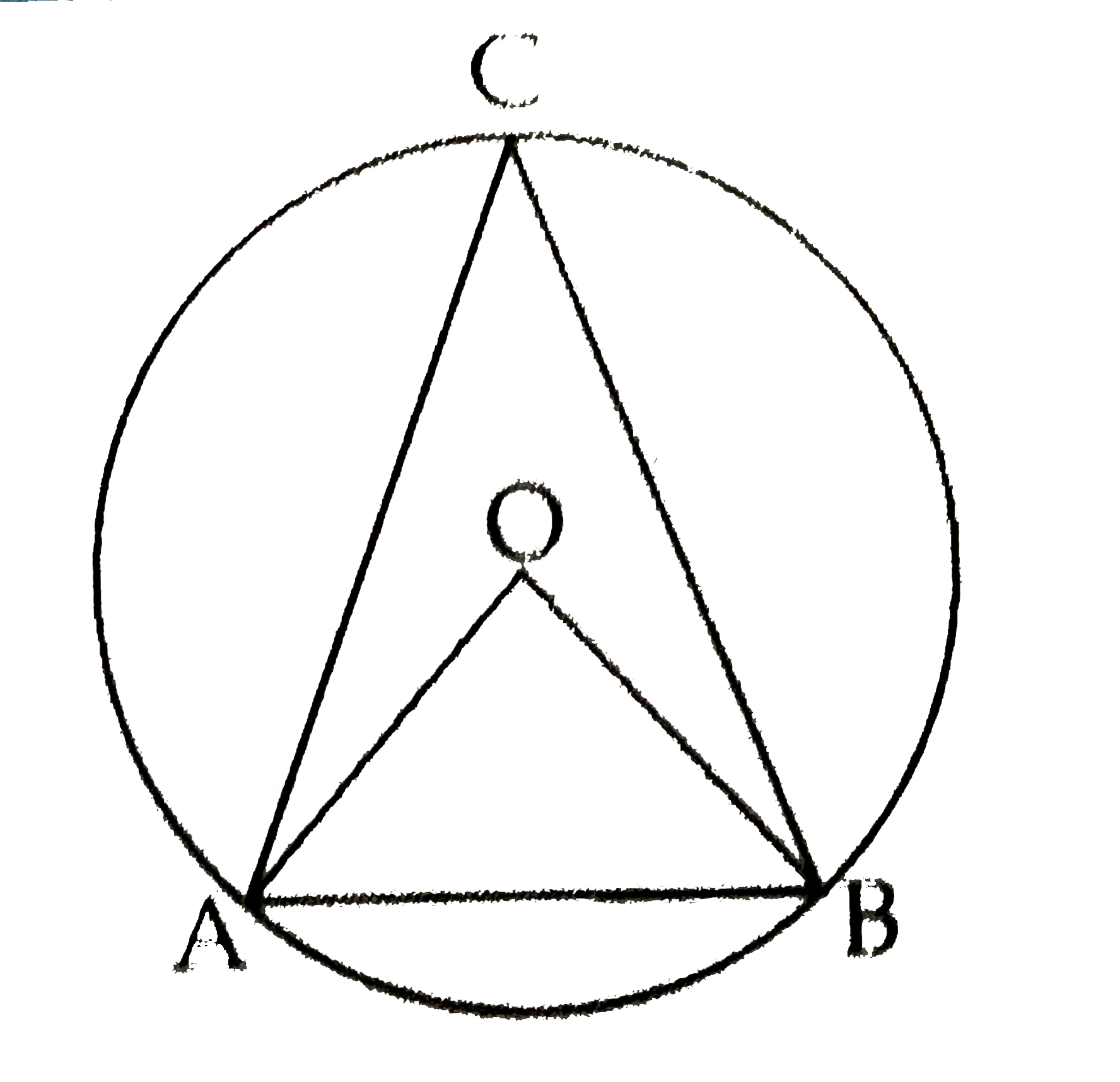
View SolutionIn the figure , in a circle with centre O, length of chord AB is equal to the radius of the circle. Find the measure of each of the following :
(1) ∠AOB
(2) ∠ACB
(3) arc AB
(4) arc ACB

View SolutionIn the abjoining figure, point O is the centre of the circle . Length of chord AB is equal to the radius of the circle . Find
(i) ∠AOB
(ii) ∠ACB
(iii) nm (arc AB)
(iv) m (arc ACB)
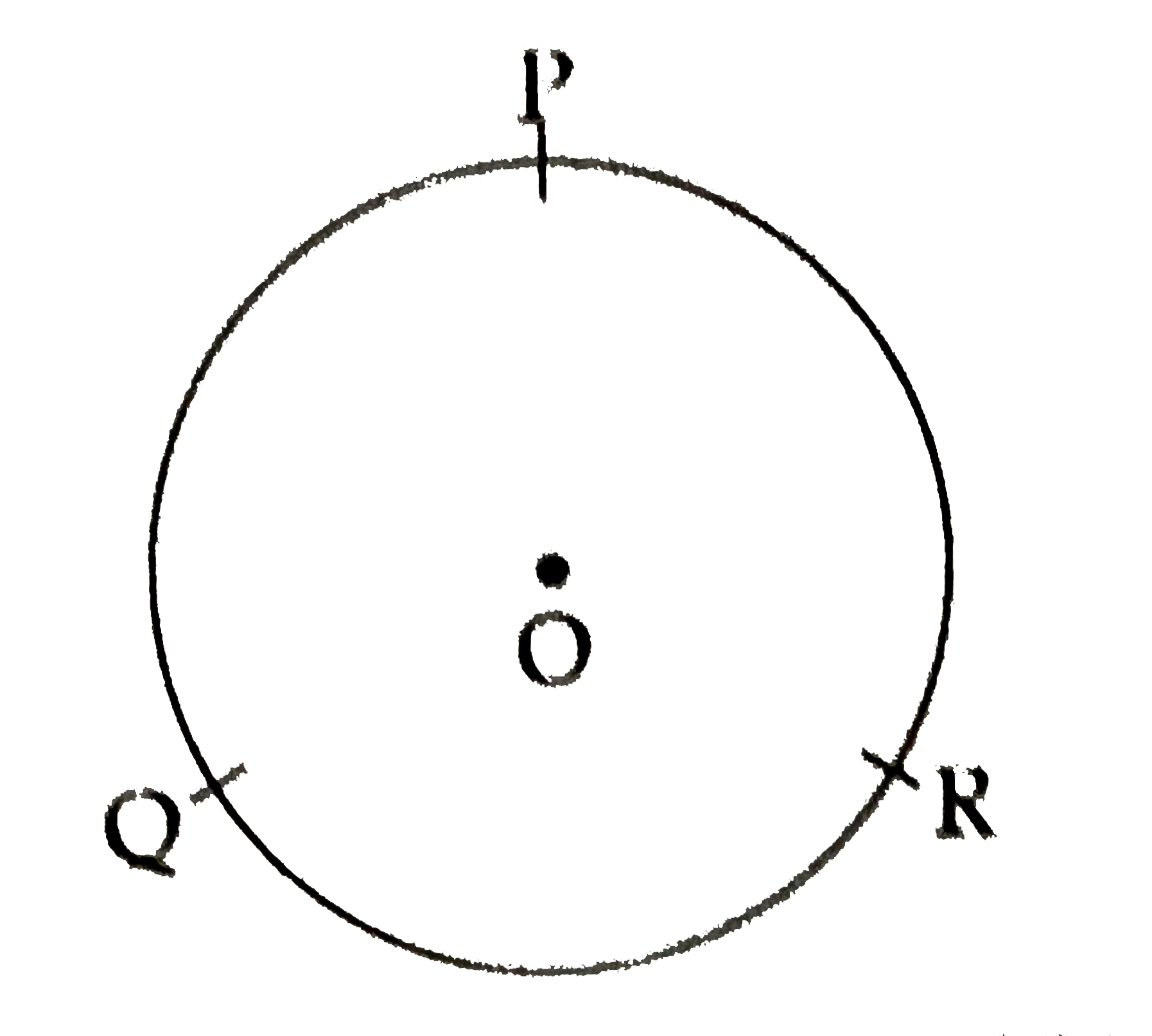
View SolutionIn the adjoining figure, a circle with centre 'O' are PQ = arc QR = arc PR . Find measure of each arc
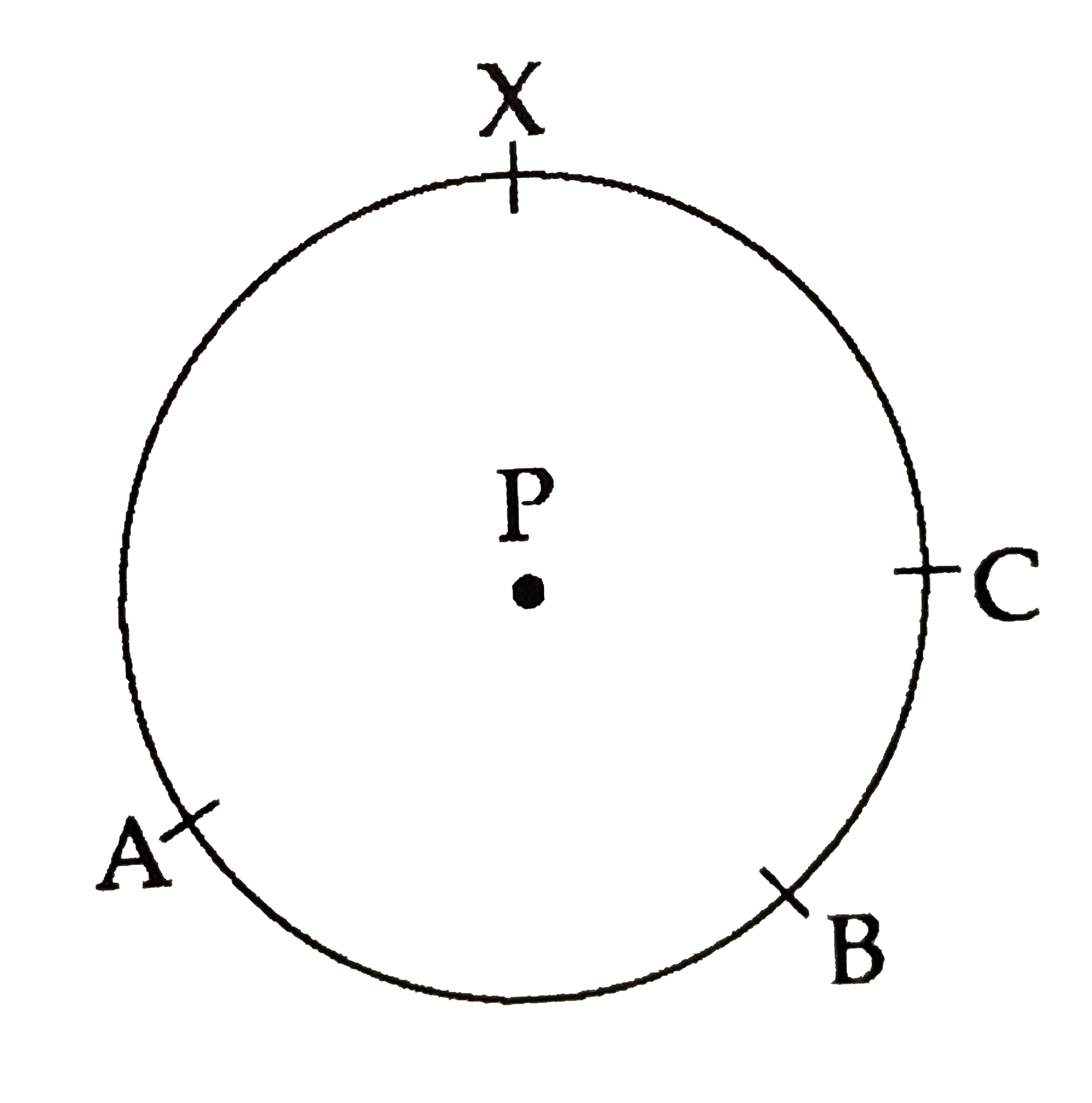
View SolutionA circle with centre P. arc AB = arc BC and arc AXC = 2 arc AB . Find measure of arc AB, arc BC and arc AXC. Prove that chord AB≅ chord BC .
View Solution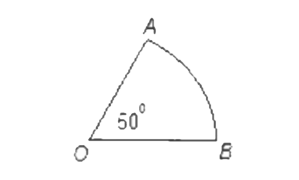
In the figure abvoe, aB is the arc of a circle with centre O. If the length of arc AB is 4π, what is the area of region OAB to the nearest tenth?
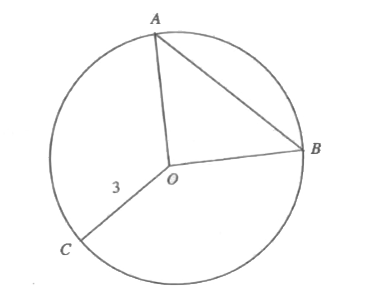
View SolutionIn the circle shown in the figure, the length of the arc ACB is 3 times the length of the arc AB. What is the length of the line segment AB ?
View Solutionचित्र मे वृत्त का केंद्र O है। वृत्त की त्रिज्या 18 सेमी है तथा ∠AOB=30∘ है, तो लघु चाप AB की लम्बाई है -
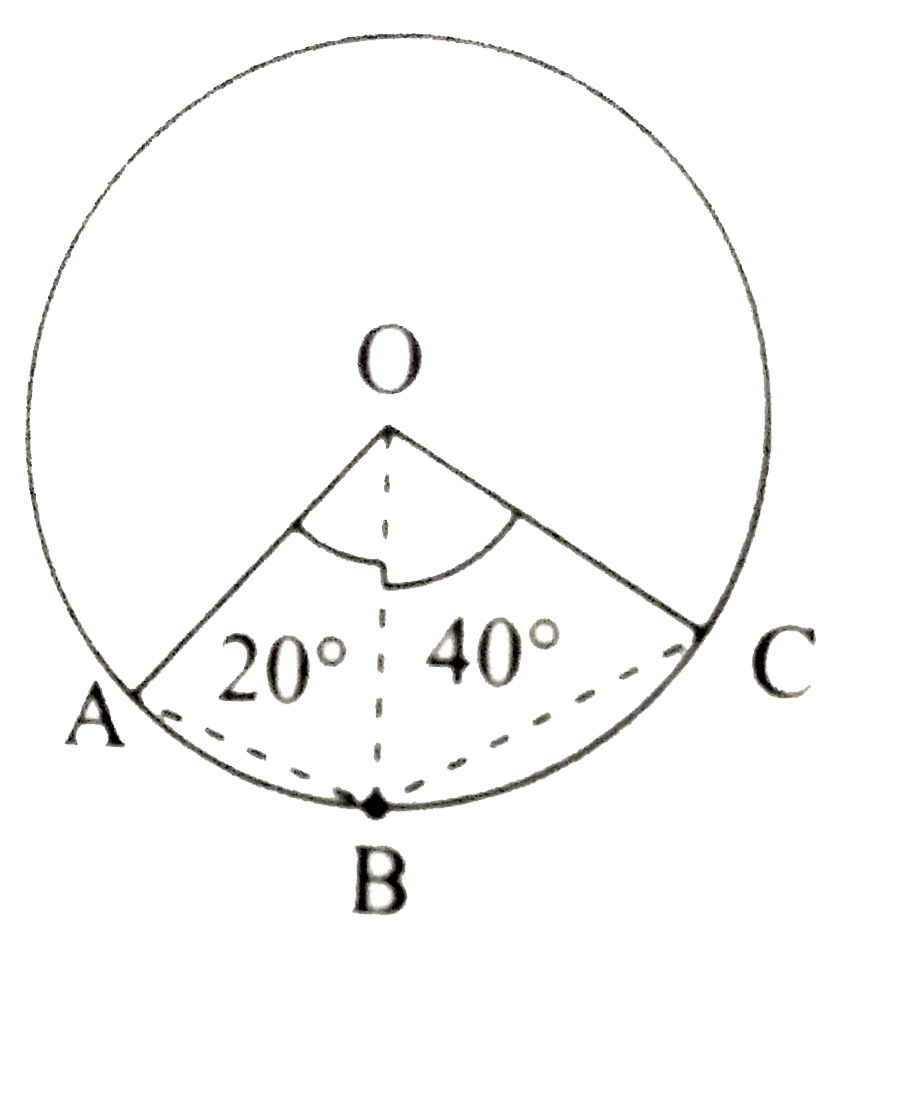
View SolutionIn,a circle, with center O, ∠AOB=20∘,∠BOC=40∘, arc BC = 4 cm.
Then length of arc AB will be . . . . . . . . .
View Solutionदी गयी आकृति में O वृत्त का केंद्र है तथा जीवाएं AB=BC है। यदि ∠BOC=80∘ है तो angleAOB का मान लिखिए।
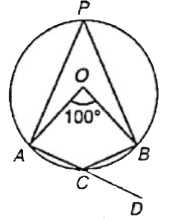
View SolutionIn the given figure, O is the centre of circle, ∠AOB=100∘. Find ∠BCD :
View Solutionचित्र में, एक वृत्त की त्रिज्या 6 सेमी है । केंद्रीय कोण 60 ∘ वाले त्रिज्याखंड के चाप AB की लम्बाई सेमी में ज्ञात कीजिए।
View Solution
