How long will a stone take to fall to the ground from the top of a building 80 m high and What will be the velocity of the stone on reaching the ground? (Take g=10m s−2)
To solve the problem of how long a stone will take to fall from the top of a building that is 80 meters high and what its velocity will be upon reaching the ground, we can follow these steps:
Step 1: Identify the known values
- Height of the building (h) = 80 m
- Initial velocity (u) = 0 m/s (since the stone is dropped)
- Acceleration due to gravity (g) = 10 m/s²
Step 2: Use the second equation of motion to find the time taken (t)
The second equation of motion is given by:
s=ut+12at2
In this case, we can substitute the known values:
- s=h=80m
- u=0m/s
- a=g=10m/s2
Substituting these into the equation:
80=0⋅t+12⋅10⋅t2
This simplifies to:
80=5t2
Step 3: Solve for t
To find t, rearrange the equation:
t2=805
t2=16
Taking the square root of both sides gives:
t=√16
t=4seconds
Step 4: Use the first equation of motion to find the final velocity (v)
The first equation of motion is given by:
v=u+at
Substituting the known values:
- u=0m/s
- a=g=10m/s2
- t=4s
Substituting these into the equation:
v=0+10⋅4
v=40m/s
Final Answers
- Time taken to fall (t) = 4 seconds
- Final velocity upon reaching the ground (v) = 40 m/s
- Height of the building (h) = 80 m
- Initial velocity (u) = 0 m/s (since the stone is dropped)
- Acceleration due to gravity (g) = 10 m/s²
The second equation of motion is given by:
s=ut+12at2
- s=h=80m
- u=0m/s
- a=g=10m/s2
80=0⋅t+12⋅10⋅t2
This simplifies to:
80=5t2
To find t, rearrange the equation:
t2=805
t2=16
Taking the square root of both sides gives:
t=√16
t=4seconds
The first equation of motion is given by:
v=u+at
- u=0m/s
- a=g=10m/s2
- t=4s
v=0+10⋅4
v=40m/s
- Time taken to fall (t) = 4 seconds
- Final velocity upon reaching the ground (v) = 40 m/s
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXAMPLES
24 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - 3(A)
19 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - TOPIC 3 (3 Marks Questions )
7 Videos
- ICSE ANNUAL EXAMINATION -2020BOOK - ICSECHAPTER - ICSE ANNUAL EXAMINATION -2020EXERCISE - SECTION-II
45 Videos
- LIGHTBOOK - ICSECHAPTER - LIGHTEXERCISE - TOPIC 2 Spherical Mirrors (4 Marks Questions )
9 Videos
Similar Questions
How much force is required to produce an acceleration of 2ms−2 in a body of mass 0.8 kg ?
View SolutionExplain giving two examples Contact forces .
View SolutionState Newton's law of gravitation.
View SolutionThe figure below shows the velocity-time graph of a body moving in a straight line.
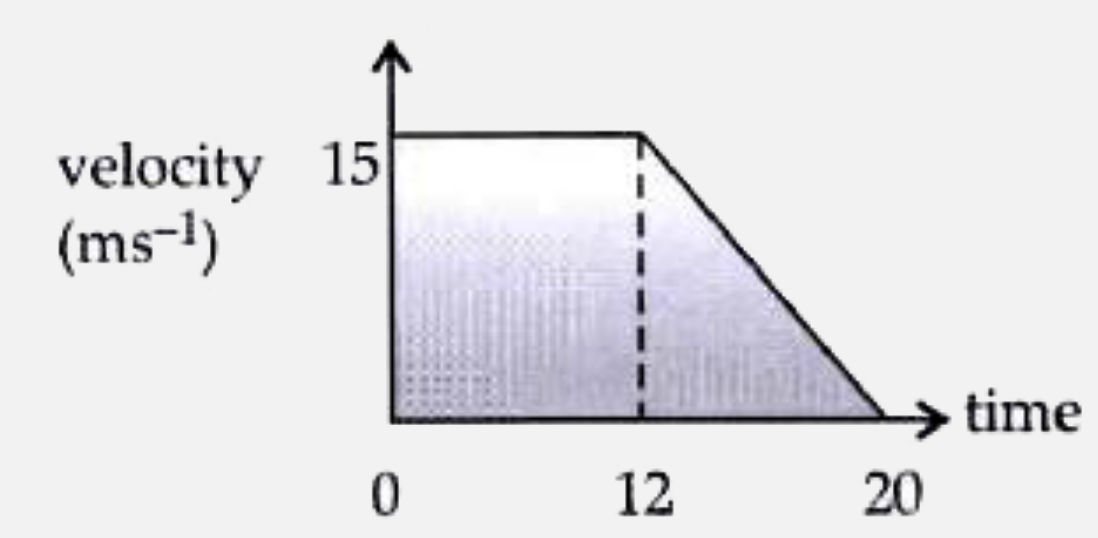
Find the time interval in which the body is moving with zero acceleration
View SolutionDifferentiate between concave mirror and convex mirror.
View SolutionA balloon is going vertically upwards with a velocity of 10 m//s . When it is 75 m above the ground, a stone is gently relesed from it. The time taken by the stone to reach the ground is (g=10 m//s^(2))
View SolutionA stone is dropped from the top of tower. When it has fallen by 5 m from the top, another stone is dropped from a point 25m below the top. If both stones reach the ground at the moment, then height of the tower from grounds is : (take g=10 m//s^(2) )
View SolutionA balloon is going upwards with a constant velocity 15m/s. When the ballooon is at 50 m height, a stone is dropped outside from the balloon. How long will stone take to reach at the ground? (take g=10m/s2)
View SolutionA balloon is going up with a uniform speed 20 m/s. It was at a height of 100 m from ground, when a stone is dropped from its basket. Find the time taken by the stone to reach the groimd and the height of the balloon from the ground, when stone hits the ground. (Take g = 10 m//s^(2) )
View SolutionA stone falls from a building and reaches the ground 2.5 seconds later. How high is the building? (=9.8m/s2)
View SolutionA stone is dropped from a height of 20 m . (i) How long will it take to reach the ground? (ii ) What will be its speed when it hits the ground? (g= 10 m//s^2)
View SolutionA stone is dropped from rest the top of a building 44.1 m high. It takes 3 s to reach the ground. Use this information to calcualte g.
View SolutionA ball is projected horizontally with a velocity of 5 m/s from the top of a building 19.6 m high. How long will the ball take to hit the ground?
View SolutionA stone falls from the top of a building and travels 53.9 m in the last second before it reaches the ground. Find the height of the building.
View SolutionA body falls from the top of a building and reaches the ground 2.5 s later. How high is the building ? (Take g = 9.8 ms−2)
View Solution
