Find dydxif2y=cosy−2x
To find dydx for the equation 2y=cos(y)−2x, we will differentiate both sides with respect to x. Here’s a step-by-step solution:
Step 1: Differentiate both sides
We start with the equation:
2y=cos(y)−2x
Now, we differentiate both sides with respect to x.
Step 2: Apply the differentiation rules
Using the chain rule and product rule, we differentiate the left side:
ddx(2y)=2dydx
For the right side, we differentiate cos(y) using the chain rule:
ddx(cos(y))=−sin(y)dydx
And the differentiation of −2x gives:
ddx(−2x)=−2
Step 3: Set up the equation
Now, we can set up the equation from our differentiation:
2dydx=−sin(y)dydx−2
Step 4: Collect terms involving dydx
We rearrange the equation to collect all terms involving dydx on one side:
2dydx+sin(y)dydx=−2
This can be factored as:
dydx(2+sin(y))=−2
Step 5: Solve for dydx
Now, we can solve for dydx:
dydx=−22+sin(y)
Final Answer
Thus, the derivative dydx is:
dydx=−22+sin(y)
---
We start with the equation:
2y=cos(y)−2x
Now, we differentiate both sides with respect to x.
Using the chain rule and product rule, we differentiate the left side:
ddx(2y)=2dydx
For the right side, we differentiate cos(y) using the chain rule:
ddx(cos(y))=−sin(y)dydx
And the differentiation of −2x gives:
ddx(−2x)=−2
Now, we can set up the equation from our differentiation:
2dydx=−sin(y)dydx−2
We rearrange the equation to collect all terms involving dydx on one side:
2dydx+sin(y)dydx=−2
This can be factored as:
dydx(2+sin(y))=−2
Now, we can solve for dydx:
dydx=−22+sin(y)
Thus, the derivative dydx is:
dydx=−22+sin(y)
Topper's Solved these Questions
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Subjective Type Questions)
3 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - FUNCTION EXERCISE 8:Questions Asked in Previous 10 Years Exams
1 Video
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
Similar Questions
Let f(x)=x+2|x+1|+x−1∣.Iff(x)=k has exactly one real solution, then the value of k is 3 (b) 0 (c) 1 (d) 2
View SolutionFind the values of x for which f(x) is positive if f(x)=x2−6x+5x2−5x+6.
View SolutionMatching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
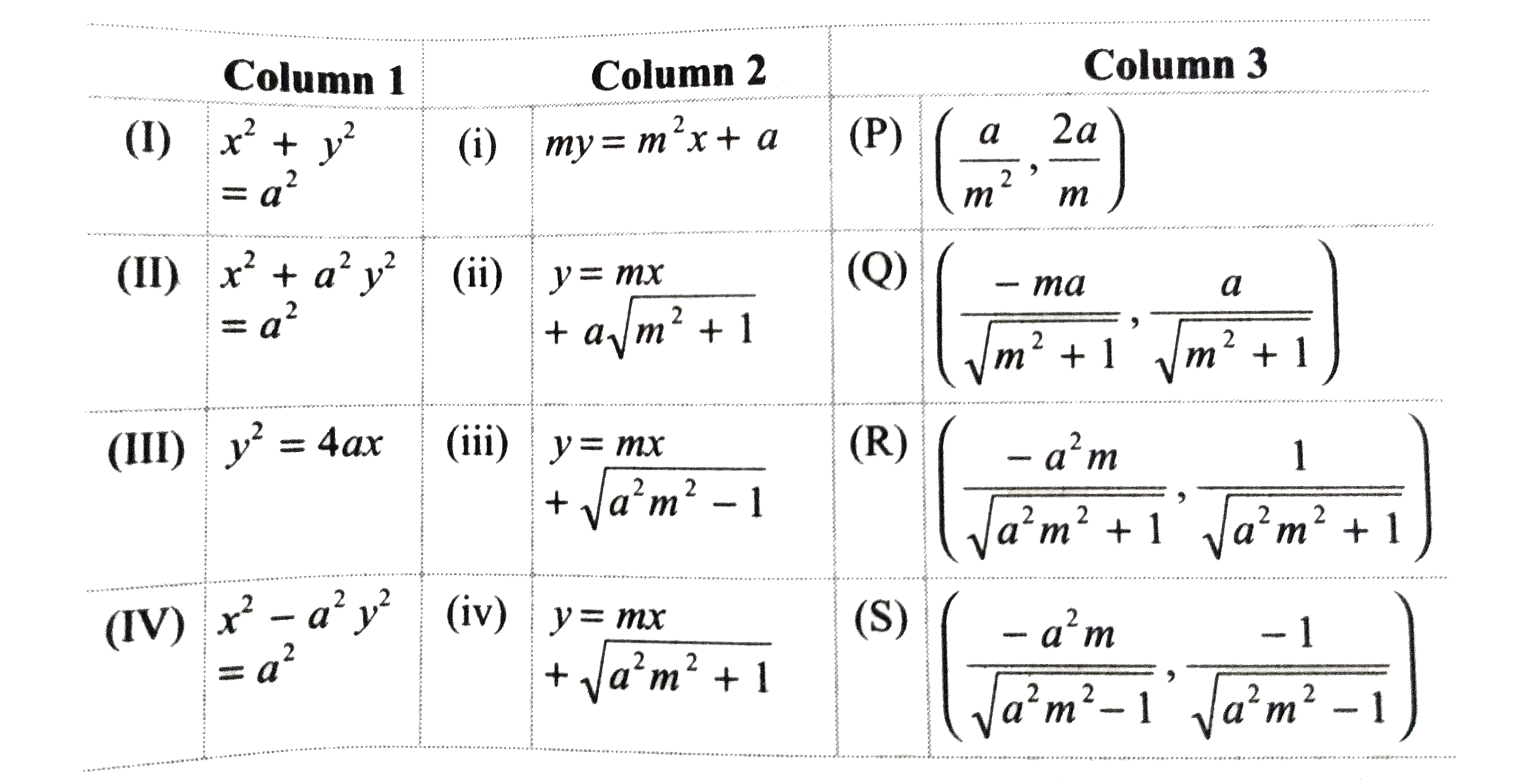
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionFind dydx if (sinx)cosy=(cosy)sinx.
View SolutionFind dy/dx in the following : ax+by^(2)=cosy
View SolutionIf (cosx)y=(cosy)x find dydx .
View SolutionFinddydxifcosy=siny+2x
View SolutionFind dydxifx=cosy
View SolutionFind dydxif3x=cosy
View SolutionFind dydxif2x−2y=siny
View SolutionFind dydx of
(cosx)y=(cosy)x
View SolutionFind dy/dx if (sinx)cosy=(cosy)sinx
View SolutionFind dydxifsinx=cosy
View SolutionFind dydxif2x−3sinx=2y
View SolutionFind dydxif2y=ey−2x
View SolutionFind dydxifx=cosy
View Solution

