iff(x)={(−x=π2,x≤−π2),(−cosx,−π2<x,≤0),(x−1,0<x≤1),(inx,x>1)
f(x) is continuous at x=−π2
f(x) is not differentiable at x = 0
f(x) is differentiable at x = 1
f(x) is differentiable at x=−π2
The correct Answer is:A, B, C, D
Step by step video solution for if f(x) ={{:(-x=(pi)/(2),xle -(pi)/(2)),(- cos x, -(pi)/(2)lt x ,le 0),( x-1, 0 lt x le 1),("in"x, x gt1):} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Statement I And Ii Type Questions)
11 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 4
3 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Single Option Correct Type Questions)
48 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHS ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
2 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
Similar Questions
Statement I f(x)=sinx+[x] is discontinuous at x = 0.
Statement II If g(x) is continuous and f(x) is discontinuous, then g(x) + f(x) will necessarily be discontinuous at x = a.
View SolutionA man leaves his home early in the morning to have a walk. He arrives at a junction of roads A and B as shown in figure. He takes the following steps in later journies :
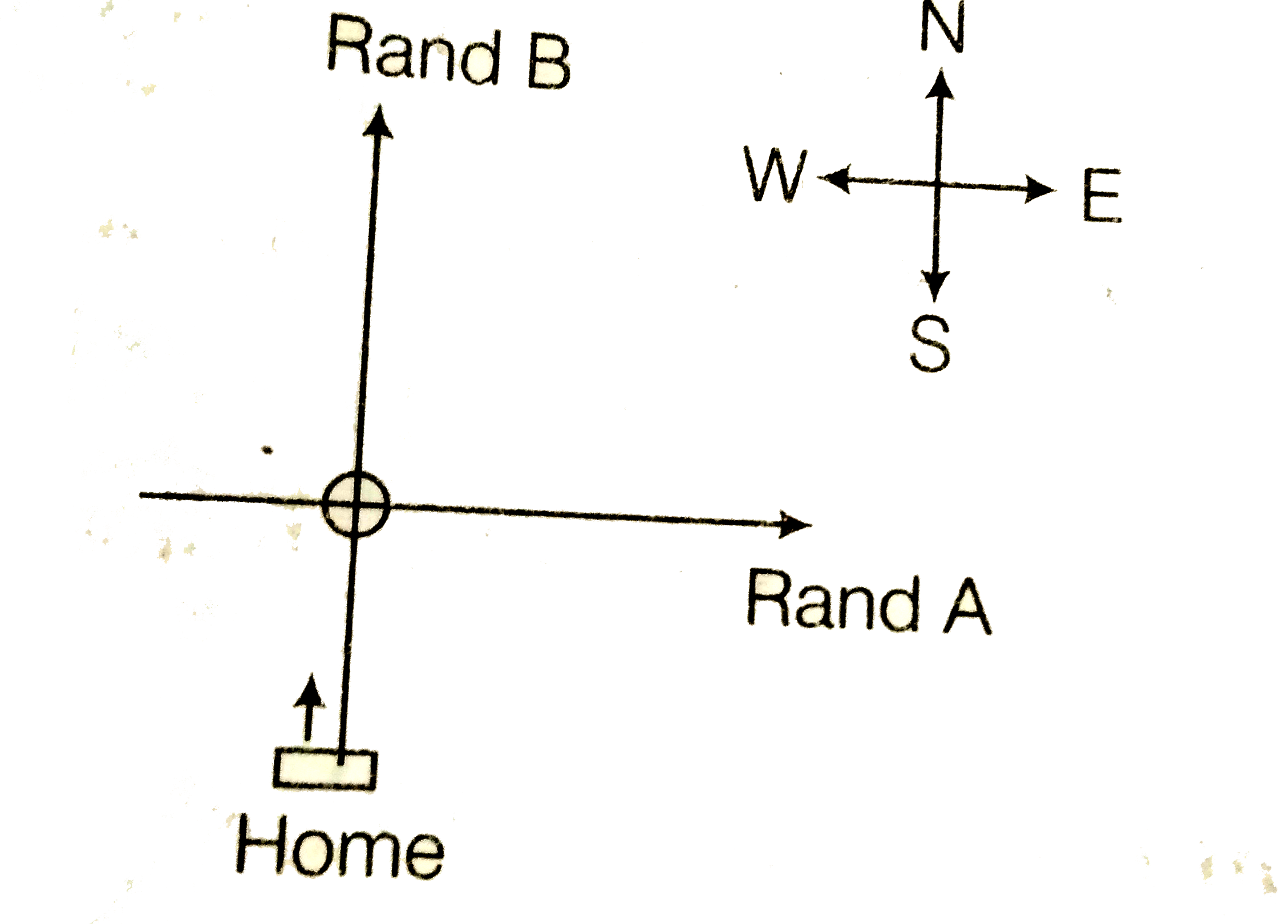
(i) 1 km in North direction.
(ii) Changes direction and moves in North-East direction for 2√2 km.
(iii) Changes direction and moves Southwards for distance of 2 km.
(iv) Finally he changes the direction and moves in South-East direction to reach road A again.
Visible/invisible path The path traced by the man in the direction parallel to road A and road B is called invisible path, the remaining path is called visible.
Visible points The point about which the man changes direction are called visible points, except the point from where he changes direction last time.
Now if roads A and B are taken as X-asix and Y-axis, then visible point representing the graph of y = f(x).
If f(x) is periodic with period 3, then f(19) is
View SolutionIf f(x)={sinπx2,x<1[x],x≥1, where [x] denotes the greatest integer function, then
View SolutionMatch the statements in Column I with those in Column II.

View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View SolutionIf f(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪⎩−x−π2 , x≤−π2−cosx , −π2<x≤0,thenx−1, 0<x≤1lnx, x>1
View SolutionIf f(x)={1x<01+sinx0≤x<π2 then derivative of f(x) x=0
View Solutionयदि f(x)={(−x−π2,,x≤−π2),(−cosx,,−π2<x≤0,),(x−1,0<x≤1) तब-
View SolutionLet f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−2sinxfor−π≤x≤−π2asinx+bfor−π2<x<π2cosxforπ2≤x≤π. If f is continuous on [−π,π), then find the values of a and b.
View SolutionIf f(x)=⎧⎨⎩sin2x√1−cos2x, for 0<x≤π2cosxπ−2x, for π2<x≤π
View SolutionLet f(x) = ⎧⎪⎨⎪⎩x3+x2−10x−1≤x<0sinx0≤x<x/21+cosxπ/2≤x≤π then f(x) has
View SolutionLet f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x3+x2−10x−1≤x<0cosx0≤x<π21+sinxπ2≤x≤x Then at x=π2, f(x) has:
View SolutionIf f(x) = {{:(-x - (pi)/(2),x le - (pi)/(2)),(-cos x,-(pi)/(2) lt x le 0),(x - 1,0 lt x le 1),(log x,x gt 1):} , Then
View Solutionमाना फलन f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩sgn(x)+x−∞<x<0−1+sinx0≤x<π2cosxπ2≤x<∞ है। बिंदु x=0 तथा x=π2 पर संततता तथा अवकलनीयता की जाँच कीजिये।
View SolutionIf f(x)= {(-x-(pi)/(2)",",x le -(pi)/(2)),(-cos x,-(pi)/(2) lt x le 0),(x-1,0 lt x le 1),(ln x,x gt 1):} Then
View SolutionIf f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩3−x+1for−1≤x<0tan(x/2)for0≤x≤πxx2−2forπ≤x≤6, then √f(0)+f(π/6)+15f(5)−123=……………..
View Solution

