letABC be a right angled triangle at C.If the inscribed circle touches the side ABat D and (AD)(BD)=11, then find the area of triangle ABC..
The correct Answer is:Now, area (ΔABC)=12ab=12(22)=11
To find the area of triangle ABC where C is the right angle, and the inscribed circle touches side AB at point D with the condition AD⋅BD=11, we can follow these steps:
Step 1: Define the segments
Let:
- AD=z
- BD=y
- CD=x
Since D is the point where the incircle touches AB, we can express the sides of triangle ABC in terms of x, y, and z:
- AB=AD+BD=z+y
- AC=AD+CD=z+x
- BC=BD+CD=y+x
Step 2: Use the given condition
We know from the problem that:
AD⋅BD=z⋅y=11
Step 3: Apply the Pythagorean theorem
Since triangle ABC is a right triangle at C, we can apply the Pythagorean theorem:
AC2+BC2=AB2
Substituting the expressions we defined:
(z+x)2+(y+x)2=(z+y)2
Step 4: Expand the equation
Expanding both sides:
(z2+2zx+x2)+(y2+2xy+x2)=(z2+2zy+y2)
Combining like terms:
z2+y2+2zx+2xy+2x2=z2+y2+2zy
Step 5: Simplify the equation
Cancelling z2 and y2 from both sides:
2zx+2xy+2x2=2zy
Dividing through by 2:
zx+xy+x2=zy
Step 6: Substitute zy with 11
Since zy=11, we can substitute this into our equation:
zx+xy+x2=11
Step 7: Rearranging for area
The area A of triangle ABC can be expressed as:
A=12×AC×BC=12×(z+x)×(y+x)
Expanding this gives:
A=12×(zy+zx+xy+x2)
Substituting zy=11:
A=12×(11+zx+xy+x2)
Step 8: Use the equation from step 6
From the equation zx+xy+x2=11:
A=12×(11+11)=12×22=11
Conclusion
Thus, the area of triangle ABC is:
11
Let:
- AD=z
- BD=y
- CD=x
- AB=AD+BD=z+y
- AC=AD+CD=z+x
- BC=BD+CD=y+x
We know from the problem that:
AD⋅BD=z⋅y=11
Since triangle ABC is a right triangle at C, we can apply the Pythagorean theorem:
AC2+BC2=AB2
Substituting the expressions we defined:
(z+x)2+(y+x)2=(z+y)2
Expanding both sides:
(z2+2zx+x2)+(y2+2xy+x2)=(z2+2zy+y2)
Combining like terms:
z2+y2+2zx+2xy+2x2=z2+y2+2zy
Cancelling z2 and y2 from both sides:
2zx+2xy+2x2=2zy
Dividing through by 2:
zx+xy+x2=zy
Since zy=11, we can substitute this into our equation:
zx+xy+x2=11
The area A of triangle ABC can be expressed as:
A=12×AC×BC=12×(z+x)×(y+x)
Expanding this gives:
A=12×(zy+zx+xy+x2)
Substituting zy=11:
A=12×(11+zx+xy+x2)
From the equation zx+xy+x2=11:
A=12×(11+11)=12×22=11
Thus, the area of triangle ABC is:
11
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Video
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Match the statements of Column I with valuwe of Column II.

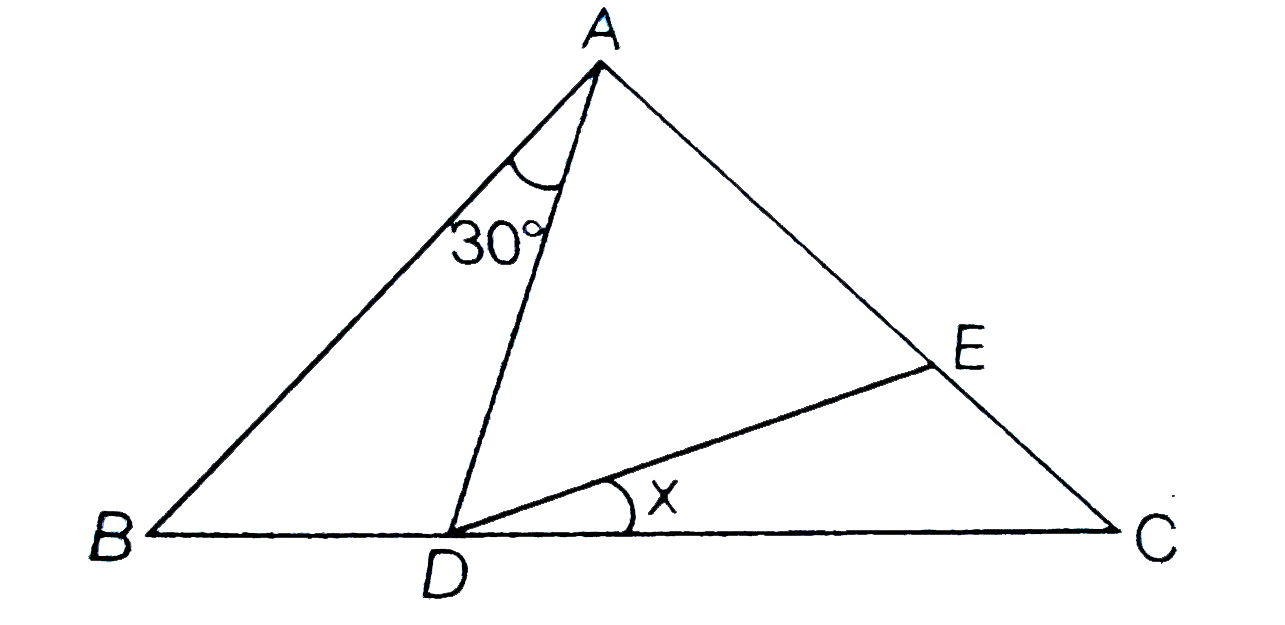
View SolutionIn the given figure,if AB=AC,∠BAD=30∘andAE=AD, then x is equal to
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionA circle is inscribed in a triangle ABC touching the side AB at D such that AD=5,BD=3,if∠A=600 then length BC equals. 9 (b)12013(c) 13(d) 12
View SolutionLet ABC be a right triangle with length of side AB=3 and hypotenuse AC=5. If D is a point on BC such that BDDC=ABAC, then AD is equal to
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
View SolutionA circumcircle is a circle which passes through all vertices of a triangle and an incircle is a circle which is inscribed in a triangle touching all sides of a triangle. Let ABC be a right-angled triangle whose radius of the circumcircle is 5 and its one side AB = 6. The radius of incircle of triangle ABC is r. Area of Delta ABC is
View SolutionA circumcircle is a circle which passes through all vertices of a triangle and an incircle is a circle which is inscribed in a triangle touching all sides of a triangle. Let ABC be a right angled triangle whose radius of circumcircle is 5 and its one side AB = 6. The radius of incircle of triangle ABC is r. The value of r is
View SolutionA circle is inscribed in a right triangle ABC, right angled at C. The circle is tangent to the segment AB at D and length of segments AD and DB are 7 and 13 respectively. Find the area of triangle ABC.
View SolutionLet ABC be a right triangle with length of side AB=3 and hyotenus AC=5. If D is a point on BC such that BDDC=ABAC, then AD is equal to
View Solutionif an equilateral triangle ABC with vertices at z1,z2andz3 be inscribed in the circle |z|=2 and again a circle is inscribed in the triangle ABC touching the sides AB, BC and CA at D(z4),E(z5)andF(z6) respectively

View SolutionLet the incircle of a ΔABC touches sides BC, CA and AB at D,E and F, respectively. Let area of ΔABC be Δ and thatof DEF be Δ'. If a, b and c are side of DetlaABC, then the value of abc(a+b+c)Δ'Δ3 is
View Solutionमाना ABC एक समकोणीय त्रिभुज है जहाँ C समकोण है। यदि अन्तःवृत AB को D स्पर्श करता है तथा (AD)(BD)=11 है तो ABC का क्षेत्रफल ज्ञात कीजिये।
View Solutionसमकोण त्रिभुज ABC कोण B पर समकोण है, तथा एक अंत: वृत्त भुजा AB, BC व AC को क्रमश F, E व D पर स्पर्श करता है, यदि BD, AC पर लम्ब है, तो AF व FB का अनुपात ज्ञात कीजिये।
View SolutionThe in circle of ΔABC touches the sides BC, CA and AB at D, E and F respectively. Then AF + BD + CE is equal to :
View Solution

