Statement I In any triangle ABC
acosA+bcosB+ccosC≤s.
Statement II In any triangle ABC
sin(A2)sin(B2)sin(C2)≤18
Both Statement I and Statement II are correct and Statement II is the correct explanation of Statement I
Both Statement I and Statement II are correct and Statement II is not the correct explanation of Statement I
Statement I is correct but Statement II is incorrect
Statement I is correct but Statement I is incorrect
The correct Answer is:A
To solve the given problem, we will analyze both statements provided and verify their validity step by step.
Step 1: Analyze Statement II
Statement II: In any triangle ABC, sin(A2)sin(B2)sin(C2)≤18.
1. Consider an equilateral triangle where A=B=C=60∘.
2. Calculate sin(A2)=sin(60∘2)=sin(30∘)=12.
3. Therefore, sin(A2)sin(B2)sin(C2)=(12)(12)(12)=18.
This shows that the maximum value of sin(A2)sin(B2)sin(C2) is indeed 18, confirming that Statement II is true.
Step 2: Analyze Statement I
Statement I: In any triangle ABC, acosA+bcosB+ccosC≤S, where S is the semi-perimeter.
1. Use the sine rule: Recall that a=2RsinA, b=2RsinB, and c=2RsinC, where R is the circumradius.
2. Substitute these into the inequality:
acosA+bcosB+ccosC=2RsinAcosA+2RsinBcosB+2RsinCcosC
3. Using the identity sinAcosA=12sin(2A), we can rewrite the expression:
=R(sin(2A)+sin(2B)+sin(2C))
4. Now, we know that sin(2A)+sin(2B)+sin(2C) is maximized in a triangle, and we can relate it to the semi-perimeter S.
5. Thus, we can conclude that acosA+bcosB+ccosC≤S holds true.
Conclusion
Both statements are verified to be true.
Statement II: In any triangle ABC, sin(A2)sin(B2)sin(C2)≤18.
2. Calculate sin(A2)=sin(60∘2)=sin(30∘)=12.
3. Therefore, sin(A2)sin(B2)sin(C2)=(12)(12)(12)=18.
Statement I: In any triangle ABC, acosA+bcosB+ccosC≤S, where S is the semi-perimeter.
2. Substitute these into the inequality:
acosA+bcosB+ccosC=2RsinAcosA+2RsinBcosB+2RsinCcosC
3. Using the identity sinAcosA=12sin(2A), we can rewrite the expression:
=R(sin(2A)+sin(2B)+sin(2C))
4. Now, we know that sin(2A)+sin(2B)+sin(2C) is maximized in a triangle, and we can relate it to the semi-perimeter S.
5. Thus, we can conclude that acosA+bcosB+ccosC≤S holds true.
Both statements are verified to be true.
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHS ENGLISHChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Passage Based Questions)
Explore 18 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHS ENGLISHChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 5: MATCHING TYPE QUESTIONS
Explore 3 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHS ENGLISHChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (More Than One Correct Option Type Questions)
Explore 23 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHS ENGLISHChapter:PRODUCT OF VECTORSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 51 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHS ENGLISHChapter:SEQUENCES AND SERIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 38 Videos
Similar Questions
R is circumradii of ΔABC,H is orthocentre, R1,R2,R3 are circumradii of ΔAHB,ΔBHC. If AH produced meet the circumradii of ABC at M and intersect BC at L,
∠AHB=180∘−C
csin(180∘−C)=2R1
csinC=2R1
R1=R
Area of ΔAHB
View SolutionMatch the statement of Colume I with values of Column II.
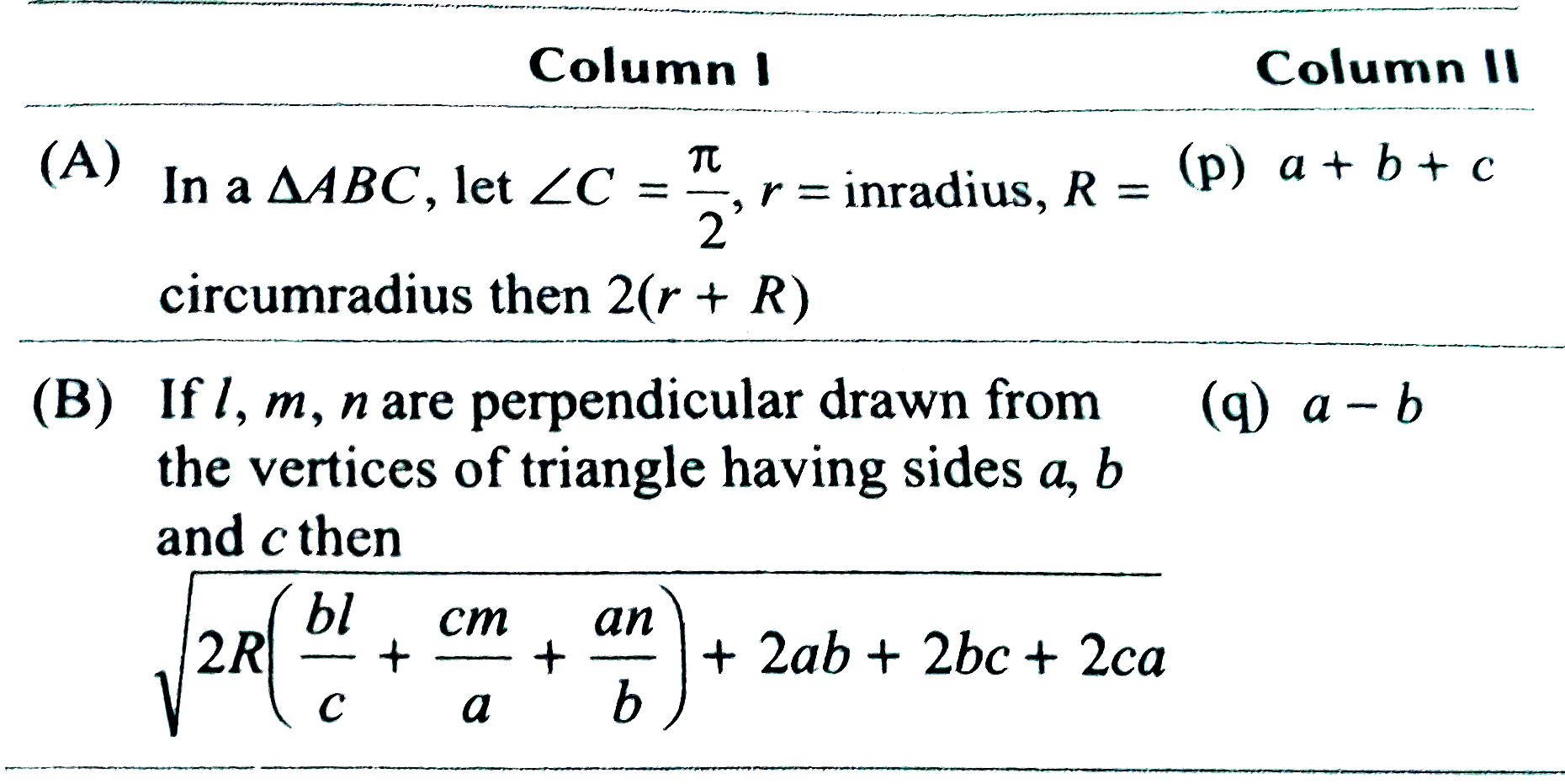
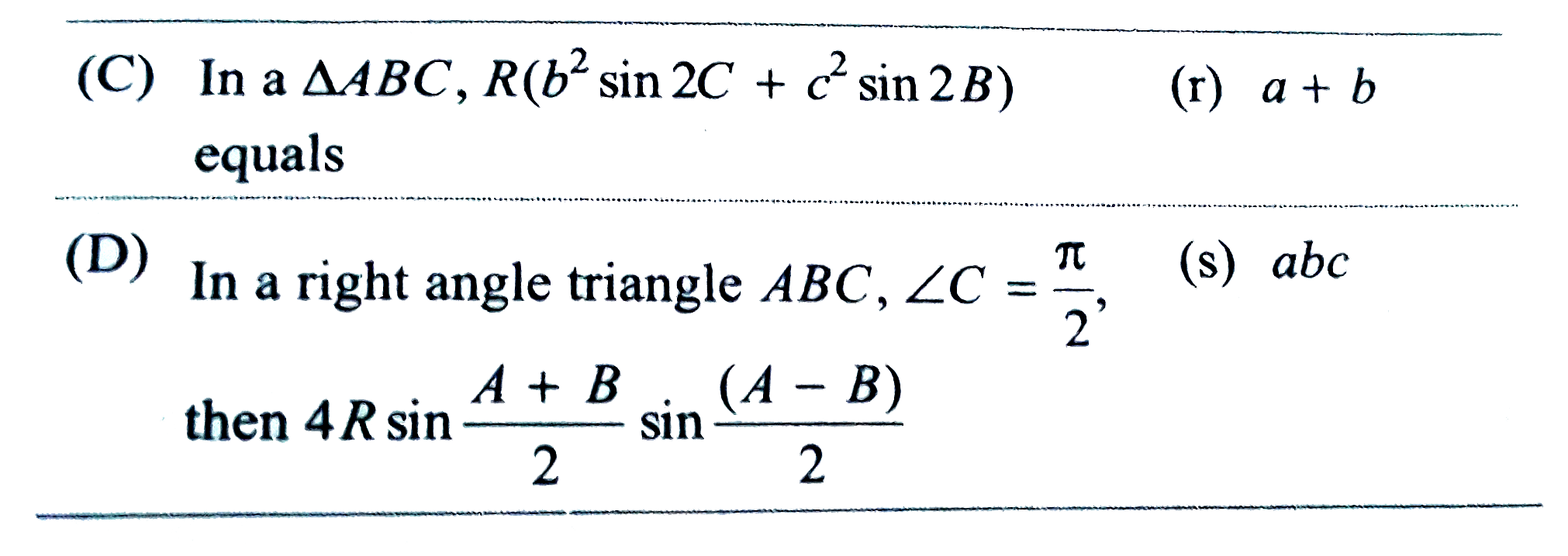
View SolutionIf area of ΔABC(Δ) and angle C are given and if c opposite to given angle is minimum, then
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionFor any triangle ABC, prove that acosA+bcosB+ccosC=2asinBsinC
View SolutionIn any triangle ABC , prove that: acosA+bcosB+ccosC=2asinBsinC
View SolutionIn Delta ABC, if sin A+sin B+sin B+sin C=1+sqrt(2) and cos A+cos B+cos C=sqrt(2) then the triangle is
View SolutionIn any ΔABC, prove that : acosA+bcosB+ccosC=2asinBsinC
View SolutionIn any triangle ABC, show that : 2acos(B2)cos(C2)=(a+b+c)sin(A2)
View SolutionIn triangle ABC, prove that sinA2sinB2sinC2≤18 and hence, prove that cosecA2+cosecB2+cosecC2≥6.
View Solutionकिसी ΔABC में सिध्द कीजिये कि:
सिध्द कीजिए कि : sinA+sinBsinC=4cos.A2cos.B2cosC2
View SolutionStatement I If in a triangle ABCsin2A+sin2B+sin2C=2, then one of the angle must be 90∘. Statement II In any triangles ABC cos2A+cos2B+cos2C=−1−4cosAcosBcosC
View SolutionStatement I In any triangle
acosA+bcosB+ccosC≤s
Statement II In any triangle sin(A2)sin(B2)sin(C2)≤18
View SolutionStatement-1: In a triangle ABC, if sin2A+sin2B+sin2C=2, then one of the angles must be 90 °.
Statement-2: In any triangle ABC
cos 2A + cos 2B + cos 2C = -1 - 4 cos A cos B cos C
View Solutionयदि A,B,C किसी ΔABC के अन्त:कोण हो तो सत्यापित कीजिए कि
(i)sin(B+C2)=cos(A2)
(ii) cos(B+C2)=sin(A2)
View Solution
