Let ABC to be an acute triangle with BC=a,CA=bandAB=c, where a≠b≠c. From any point 'p' inside ΔABC≤tB,E,F denot foot of perpendiculars form 'p' noto the sides, BC, CA and AB, respectively. Now, answer the following equations.
If ΔDEF is equilateral, then 'P'
the incircle of ΔABC
line of intternal angle bisectors from A, B and C
arcs of 3 circles
None of the above
The correct Answer is:C
Step by step video solution for Let ABC to be an acute triangle with BC=a,CA =b and AB=c, where a ne b ne c. From any point 'p' inside Delta ABClet B,E,F denot foot of perpendiculars form 'p' noto the sides, BC, CA and AB, respectively. Now, answer the following equations. If DeltaDEF is equilateral, then 'P' by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHS ENGLISHChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 5: MATCHING TYPE QUESTIONS
Explore 3 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHS ENGLISHChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Single Integer Answer Type Questions)
Explore 15 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHS ENGLISHChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Statement I And Ii Type Questions)
Explore 11 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHS ENGLISHChapter:PRODUCT OF VECTORSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 51 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHS ENGLISHChapter:SEQUENCES AND SERIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 38 Videos
Similar Questions
Match the statement of Colume I with values of Column II.
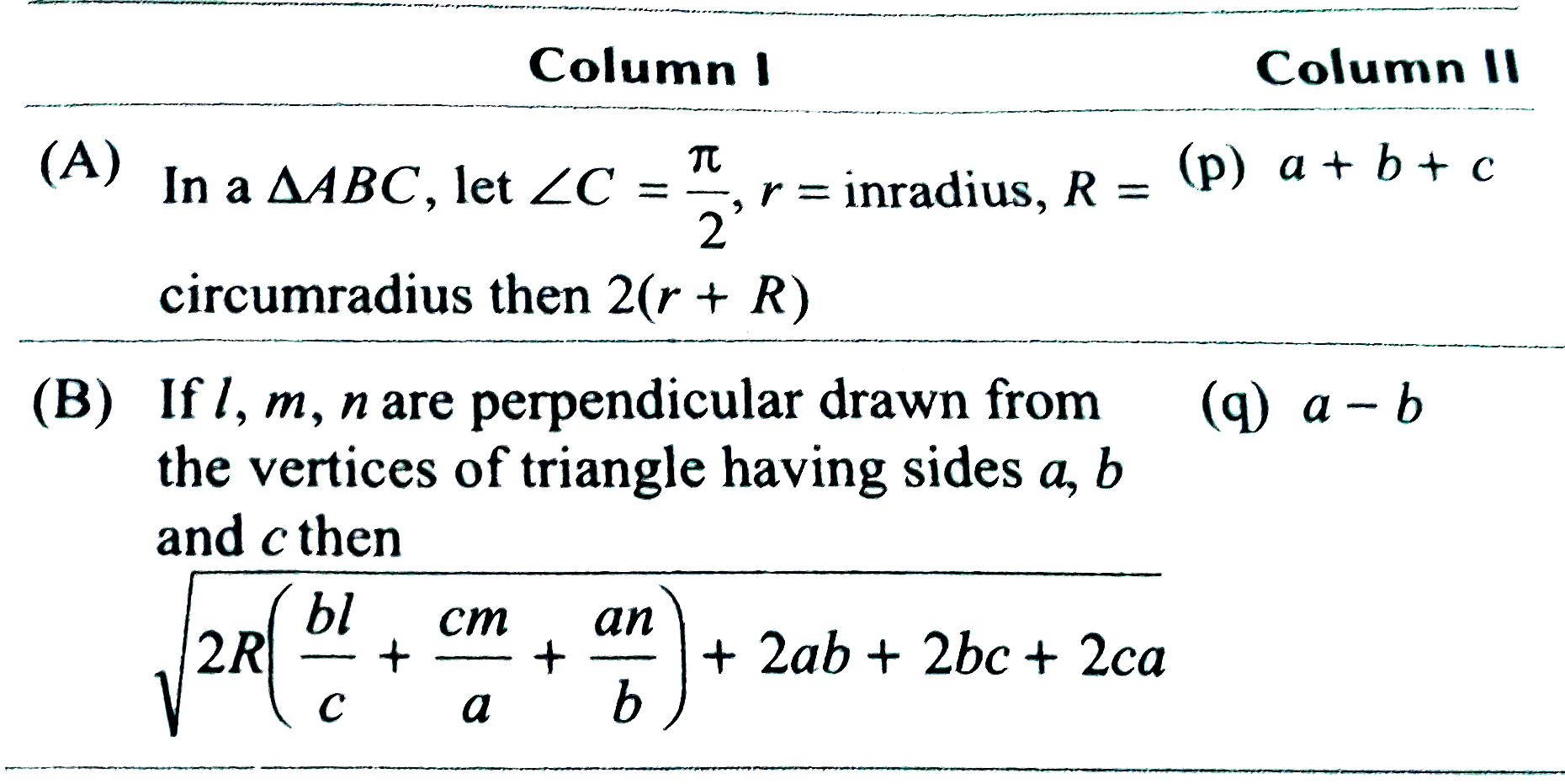
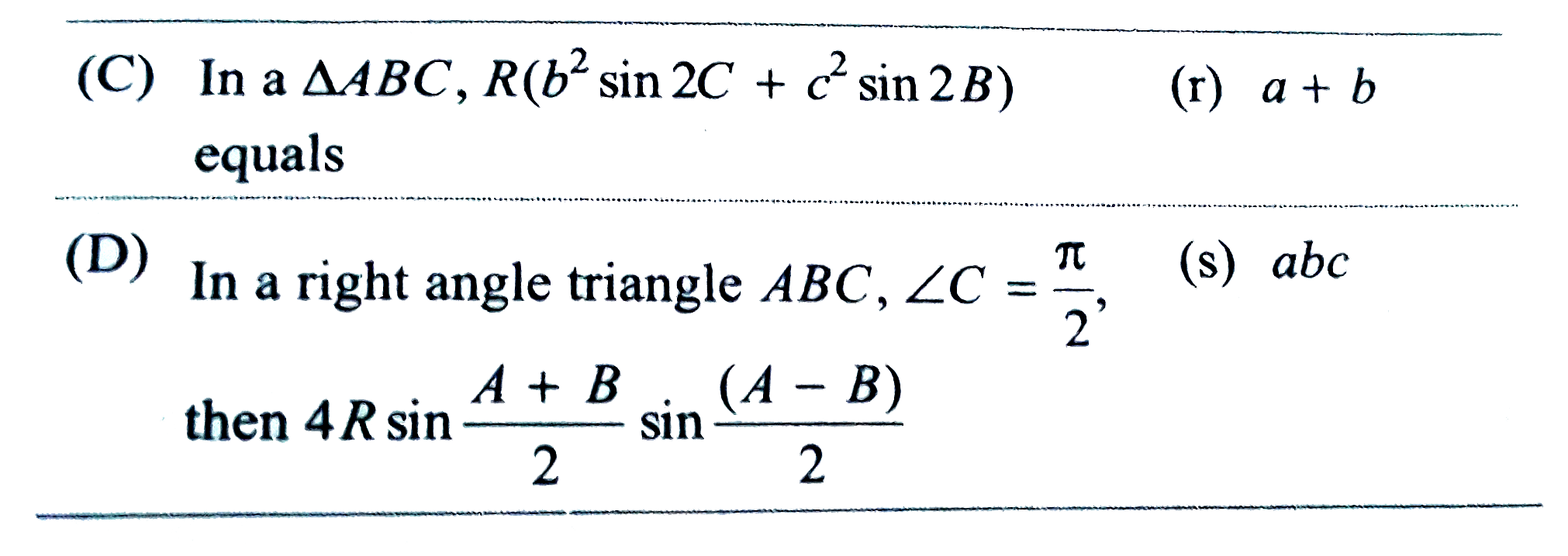
View SolutionIf in ΔABC,∠C=π8,a=√2andb=√2+√2 then find the measure of angle A (in degree).
View SolutionIn a triangle ABC,a3+b3+c3=c2(a+b+c) (All symbol used have usual meaning in a triangle.) Statement-1: The value of ∠C=60∘. Statement-2: ΔABC must be equilateral.
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionABC is right angle triangle at C. Let BC=a ,CA=b,AB=c and Let 'P' be the length of perpendicular from C to AB.prove that (1)/(p^(2))=(1)/(a^(2))+(1)/(b^(2))
View SolutionD,E,F are the foot of the perpendiculars from vertices A,B,C to sides BC,CA,AB respectively,and H is the or the centre of acute angled triangle ABC, where a,b,c are the sides of triangle ABC, then
View SolutionLet vec a,vec b,vec c form sides BC,CA and AB respectively of a triangle ABC then
View Solutionआकृति में समबाहु त्रिभुज ABC की भुजाओं BC,CA तथा AB में मध्य बिंदु क्रमशः D,E तथा F है । सिद्ध कीजिए कि ΔDEF भी एक समबाहु त्रिभुज है।
View SolutionLet ABC to be an acute triangle with BC=a,CA=bandAB=c, where a≠b≠c. From any point 'p' inside ΔABC≤tB,E,F denot foot of perpendiculars form 'p' noto the sides, BC, CA and AB, respectively. Now, answer the following equations.
All positions of point 'p' for which ΔBEF is isosceles lie on
View SolutionLet ABC to be an acute triangle with BC=a,CA=bandAB=c, where a≠b≠c. From any point 'p' inside ΔABC≤tB,E,F denot foot of perpendiculars form 'p' noto the sides, BC, CA and AB, respectively. Now, answer the following equations.
Let (A(7,0),B(4,4)andC(0,0)andΔDEF is isosceles with DE=DF. Then, the curve on which 'P' may lie
View SolutionLet ABC to be an acute triangle with BC=a,CA=bandAB=c, where a≠b≠c. From any point 'p' inside ΔABC≤tB,E,F denot foot of perpendiculars form 'p' noto the sides, BC, CA and AB, respectively. Now, answer the following equations.
If ΔDEF is equilateral, then 'P'
View Solutionयदि किसी त्रिभुज ABC की भुजाओं BC,CA,व AB के मध्य बिन्दु क्रमशः D,E, व F हो, तो ΔDEF निम्न में से किस त्रिभुज के सर्वांगसम होगा :
View SolutionABC is a right Triangle right angled at C. Let BC=a,CA=b,AB=c and let p be the length of the perpendicular fromt C on AB Prove that1p2=1a2+1b2.
View SolutionABC is a right angled triangle which is right angled at C. Let AB=c, BC=a, CA=b and let p be the length of perpendicular from C and AB. Prove that c=abp.
View SolutionABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
View Solution
