Evaluate: ∫log(1+x2) dx
The correct Answer is:xlog(x2+1)−2x+2tan−1x+C
Step by step video solution for Evaluate: intlog(1+x^2)\ dx by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHS ENGLISHCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise For Session 5
10 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHS ENGLISHCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise For Session 6
10 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHS ENGLISHCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise For Session 3
22 Videos
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
Similar Questions
Evaluate the following Integrals :
∫x2(x−1)(x−2)(x−3)dx
View SolutionEvaluate the following Integrals :
∫x4−1x2(x4+x2+1)1/2dx
View SolutionEvaluate the following integrals
∫xdx9−16x4
View SolutionMatching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
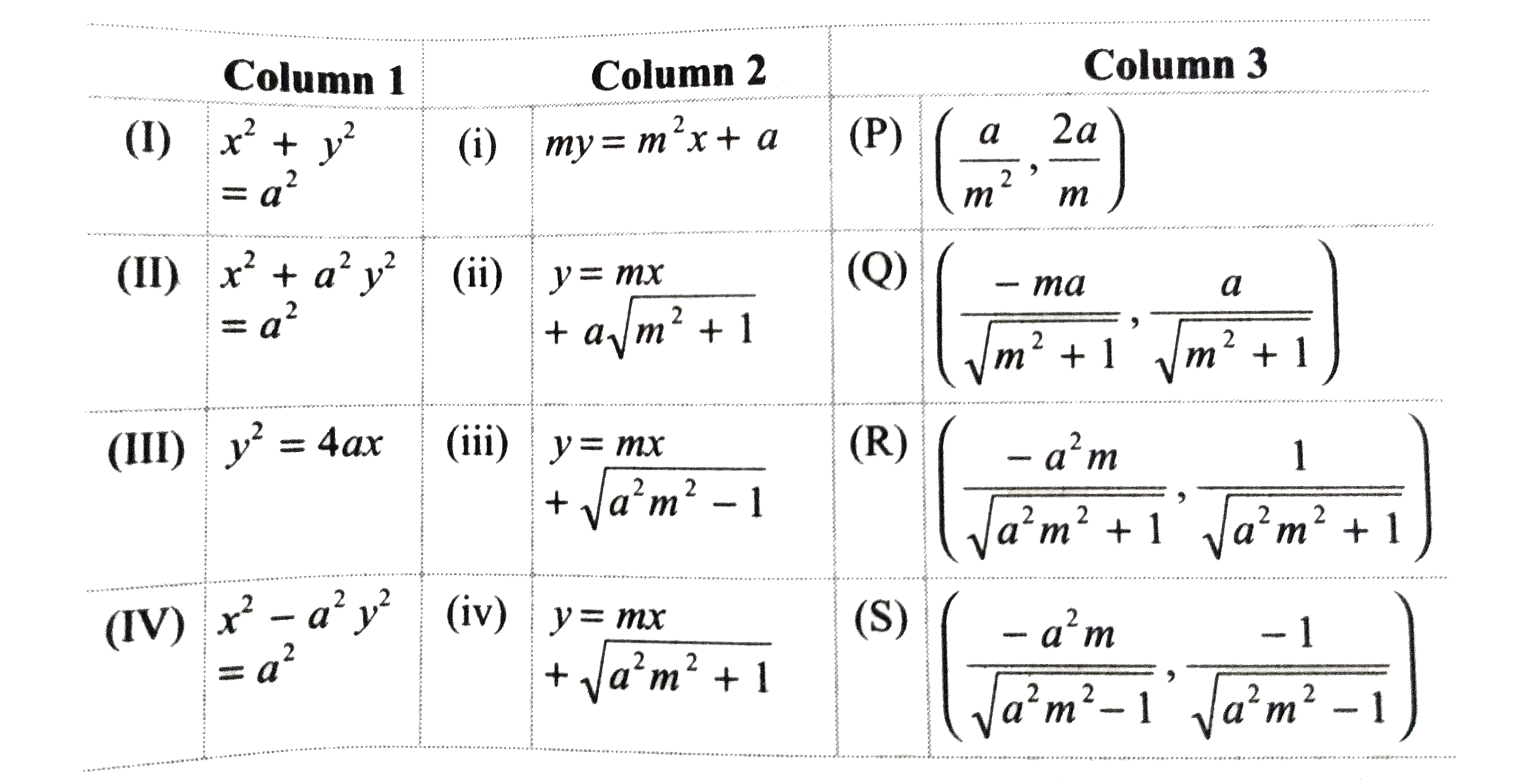
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionEvaluate: ∫log(x+1)dx
View SolutionEvaluate: ∫log(2+x2)dx
View Solution∫log(1−x2)dx
View Solution∫log(1+x2)dx.
View Solutionज्ञात कीजिए ∫log(x2+1)dx.
View SolutionEvaluate : ∫log(1+x2)dx
View Solution∫log(2+x2)dx का मान ज्ञात कीजिए |
View SolutionFind ∫log(x2+2)dx.
View SolutionEvaluate: ∫log(x2)dx
View SolutionEvaluate: ∫log(1+x2) dx
View SolutionEvaluate: ∫log(x+1) dx
View Solution

