Let Im,n=∫sinnxcosmxdx. Then , we can relate In,m with each of the following :
(i) In−2,m (ii)In+2,m
(iii) In,m−2 (iv)In,m+2
(v) In−2,m+2 In+2,m−2
Suppose we want to establish a relation between In,m and In,m−2, then we get
P(x)=sinn+1xcosm−1x ...(i)
In In,m and In,m−2 the exponent of cos x in m and m−2 respectively, the minimum of the two is m - 2, adding 1 to the minimum we get m−2+1=m−1. Now, choose the exponent of sin x for m - 1 of cos x in P(x). Similarly, choose the exponent of sin x for
P(x)=(nH)sinnxcosmx−(m−1)sinn+2xcosm−2x.
Now, differentiating both the sides of Eq. (i), we get
=(n+1)sinnxcosmx−(m−1)sinnx(1−cos2x)cosm−2x
=(n+1)sinnxcosmx−(m−1)sinnxcosm−2x+(m−1)sinnxcosnx
=(n+m)sinnxcosmx−(m−1)sinnxcosm−2x
Now, integrating both the sides, we get
sinn+1xcosm−1x=(n+m)In,m−(m−1)In,m−2
Similarly, we can establish the other relations.
The relation I4,2 and I4,4 is
I4,2=13(sin5xcos3x+8I4,4)
I4,2=13(−sin5xcos3x+8I4,4)
I4,2=13(sin5xcos3x−8I4,4)
I4,2=13(sin5xcos3x+6I4,4)
The correct Answer is:B
To establish the relation between I4,2 and I4,4, we start with the definitions of the integrals:
Im,n=∫sinnxcosmxdx
Step 1: Define P(x)
We define:
P(x)=sinn+1xcosm−1x
For our case, we have n=4 and m=4.
Step 2: Differentiate P(x)
Now, we differentiate P(x):
dPdx=(n+1)sinnxcosm−1xcosx−(m−1)sinn+1xsinxcosm−2x
Substituting n=4 and m=4:
dPdx=5sin4xcos3x−3sin5xcos2x
Step 3: Rewrite the Derivative
We can rewrite the derivative as:
dPdx=5sin4xcos3x−3sin5xcos2x
Step 4: Integrate Both Sides
Integrating both sides gives us:
P(x)=5I4,3−3I5,2
Step 5: Substitute Back for P(x)
Substituting back for P(x):
sin5xcos3x=5I4,3−3I5,2
Step 6: Establish the Relation
Now, we need to relate I4,2 and I4,4. We can express I4,2 in terms of I4,4:
I4,4=∫sin4xcos4xdx
I4,2=∫sin4xcos2xdx
Final Relation
From our previous steps, we can derive:
I4,2=13(5I4,4−P(x))
This gives us the relation between I4,2 and I4,4.
I4,2=∫sin4xcos2xdx
Topper's Solved these Questions
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise (Single Integer Answer Type Questions)
Explore 12 Videos
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise (Subjective Type Questions)
Explore 14 Videos
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise (Statement I And Ii Type Questions)
Explore 4 Videos
- HYPERBOLABook:ARIHANT MATHS ENGLISHChapter:HYPERBOLAExercise:Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
Explore 3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:ARIHANT MATHS ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 8 Videos
Similar Questions
If ∫(2x+3)dxx(x+1)(x+2)(x+3)+1=C−1f(x) where f(x) is of the form of ax2+bx+c, then the value of f(1) is
View SolutionThe value of
∫e(xsinx+cosx).(x4cos3x−xsinx+cosxx2cos2x)dx, is equal to
View SolutionStatement I Integral of an even function is not always an odd function. Statement II Integral of an odd function is an even function .
View SolutionMatching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
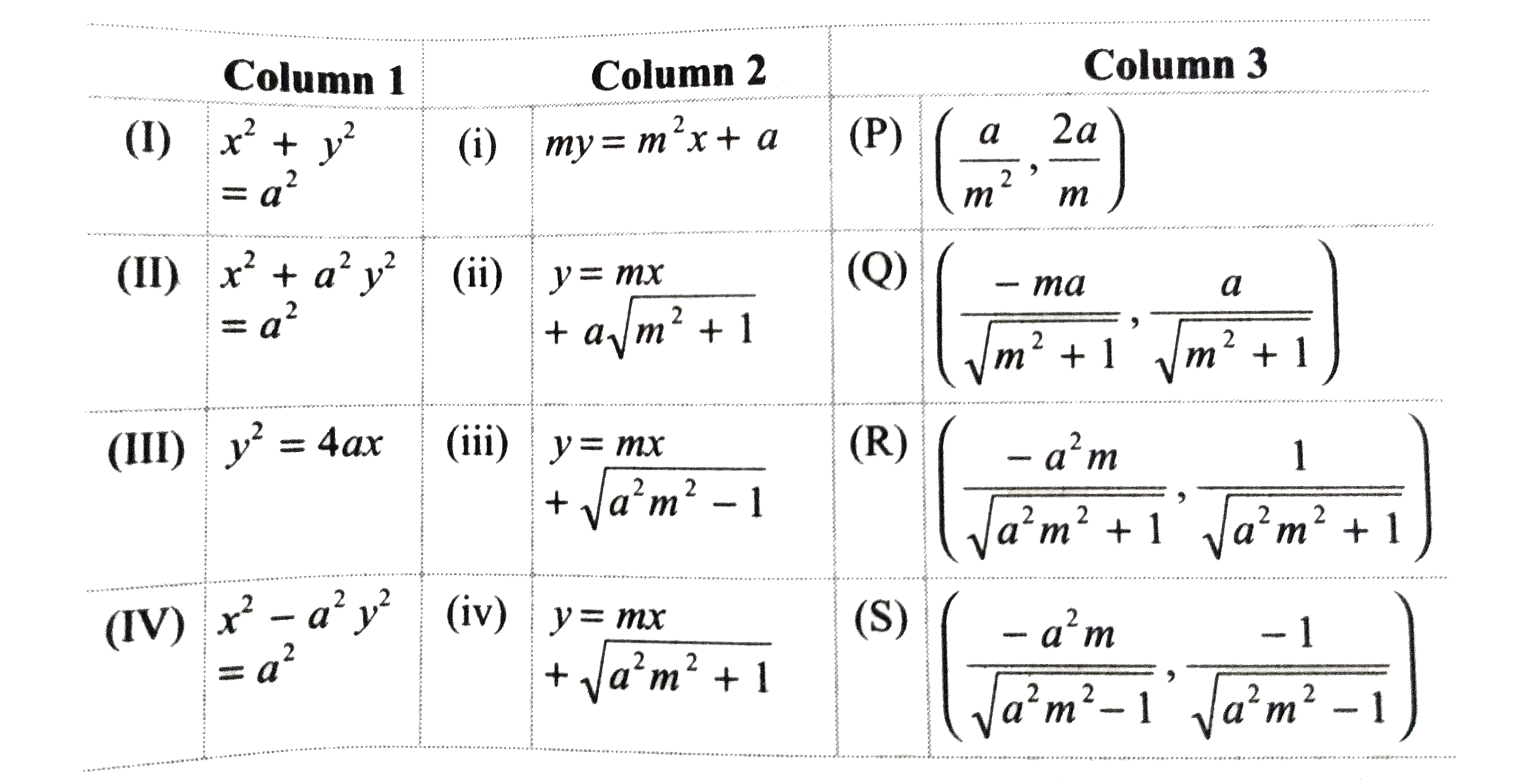
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View Solutionif I_(m,n)=int(x^(m))/((log x)^(n))dx, then (m+1)I_(m,n)-nI_(m,n+1) is
View SolutionIf I_(m,n)=int cos^(m)x sin nxdx=f(m,n)I_(m-1)-(cos^(m)x cos nx)/(m+n), then f(m,n)=
View SolutionLet I_(n)=int(x^(n))/(sqrt(x^(2)+2x+5))dx then I_(n)=(x^(m-1))/(n)sqrt(x^(2)+2x+5)-lambda I_(n-1)-mu I_(n-2) where lambda,mu and m' are involving n' then
View SolutionIf Im,n=∫π20sinmxcosnxdx then show that Im,n=m−1m+nIm−2,n and find Im,n in terms of different combinations of m and n.
View SolutionComprehension 1
Let In,m=∫sinnxcosmx.dx. Then we can relate In,m with each of the following
i) In−2,m, ii) In+2,m, iii) In,m−2
iv) In,m−2, v) In−2,m+2, vi) In+2,m−2
Suppose we want to establish a relation between In,m and In,m−2, then we set
P(x)=sinn+1xcosm−1x................(1)
In In,m and In,m−2 the exponent of cosx is m and m−2+1=m−1. Now choose the exponent m−1 of cosx in P(x). Similarly choose hte exponent of sinx for P(x).
Now, differentiating both sides of (1), we get
P′(x)=(n+1)sinnxcosmX−(m−1)sinn+2Xcosm−2X
=(n+1)sinnXcosmX−(m−1)sinnx(1−cos2x)cosm−2X
=(n+1)sinnXcosmX−(m−1)sinnXcosm−2X+(m−1)sinnXcosmX
=(n+m)sinnXcosmX−(m−1)sinnXcosm−2X
Now, integrating both sides, we get
sinn+1cosm−1x=(n+m)In,m−(m−1)In,m+2
Similarly, we can establish the other relations.
The relation between I4,2 and I2,2 is
View SolutionIf Im,n=∫(sinx)m(cosx)ndx then prove that Im,n=(sinx)m+1(cosx)n−1m+n+n−1m+n.Im,n−2
View SolutionIf Im,n=∫cosmx⋅cosnxdx, show that (m+n)Im,n=cosmx⋅sinnx+mI(m−1,n−1)
View SolutionLet Im,n=∫sinnxcosmxdx. Then , we can relate In,m with each of the following :
(i) In−2,m (ii)In+2,m
(iii) In,m−2 (iv)In,m+2
(v) In−2,m+2 In+2,m−2
Suppose we want to establish a relation between In,m and In,m−2, then we get
P(x)=sinn+1xcosm−1x ...(i)
In In,m and In,m−2 the exponent of cos x in m and m−2 respectively, the minimum of the two is m - 2, adding 1 to the minimum we get m−2+1=m−1. Now, choose the exponent of sin x for m - 1 of cos x in P(x). Similarly, choose the exponent of sin x for
P(x)=(nH)sinnxcosmx−(m−1)sinn+2xcosm−2x.
Now, differentiating both the sides of Eq. (i), we get
=(n+1)sinnxcosmx−(m−1)sinnx(1−cos2x)cosm−2x
=(n+1)sinnxcosmx−(m−1)sinnxcosm−2x+(m−1)sinnxcosnx
=(n+m)sinnxcosmx−(m−1)sinnxcosm−2x
Now, integrating both the sides, we get
sinn+1xcosm−1x=(n+m)In,m−(m−1)In,m−2
Similarly, we can establish the other relations.
The relation between I4,2 and I2,2 is
View SolutionLet Im,n=∫sinnxcosmxdx. Then , we can relate In,m with each of the following :
(i) In−2,m (ii)In+2,m
(iii) In,m−2 (iv)In,m+2
(v) In−2,m+2 In+2,m−2
Suppose we want to establish a relation between In,m and In,m−2, then we get
P(x)=sinn+1xcosm−1x ...(i)
In In,m and In,m−2 the exponent of cos x in m and m−2 respectively, the minimum of the two is m - 2, adding 1 to the minimum we get m−2+1=m−1. Now, choose the exponent of sin x for m - 1 of cos x in P(x). Similarly, choose the exponent of sin x for
P(x)=(nH)sinnxcosmx−(m−1)sinn+2xcosm−2x.
Now, differentiating both the sides of Eq. (i), we get
=(n+1)sinnxcosmx−(m−1)sinnx(1−cos2x)cosm−2x
=(n+1)sinnxcosmx−(m−1)sinnxcosm−2x+(m−1)sinnxcosnx
=(n+m)sinnxcosmx−(m−1)sinnxcosm−2x
Now, integrating both the sides, we get
sinn+1xcosm−1x=(n+m)In,m−(m−1)In,m−2
Similarly, we can establish the other relations.
The relation between I4,2 and I6,2 is
View SolutionLet Im,n=∫sinnxcosmxdx. Then , we can relate In,m with each of the following :
(i) In−2,m (ii)In+2,m
(iii) In,m−2 (iv)In,m+2
(v) In−2,m+2 In+2,m−2
Suppose we want to establish a relation between In,m and In,m−2, then we get
P(x)=sinn+1xcosm−1x ...(i)
In In,m and In,m−2 the exponent of cos x in m and m−2 respectively, the minimum of the two is m - 2, adding 1 to the minimum we get m−2+1=m−1. Now, choose the exponent of sin x for m - 1 of cos x in P(x). Similarly, choose the exponent of sin x for
P(x)=(nH)sinnxcosmx−(m−1)sinn+2xcosm−2x.
Now, differentiating both the sides of Eq. (i), we get
=(n+1)sinnxcosmx−(m−1)sinnx(1−cos2x)cosm−2x
=(n+1)sinnxcosmx−(m−1)sinnxcosm−2x+(m−1)sinnxcosnx
=(n+m)sinnxcosmx−(m−1)sinnxcosm−2x
Now, integrating both the sides, we get
sinn+1xcosm−1x=(n+m)In,m−(m−1)In,m−2
Similarly, we can establish the other relations.
The relation I4,2 and I4,4 is
View SolutionIf Imc=∫emx.Xndx, then Imn+nmIm,n−1=
View Solution
