If ∫ex3+x2−1(3x4+2x3+2x)dx=f(x)+C, then the value of f(1)×f(−1) is−.
The correct Answer is:1
Step by step video solution for "If " int e^(x^(3)+x^(2)-1)(3x^(4)+2x^(3)+2x)dx=f(x)+C, " then the value of " f(1)xxf(-1) " is"-. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHS ENGLISHCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Subjective Type Questions)
14 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHS ENGLISHCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHS ENGLISHCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Passage Based Questions)
11 Videos
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
Similar Questions
The value of
∫e(xsinx+cosx).(x4cos3x−xsinx+cosxx2cos2x)dx, is equal to
View SolutionThe integral ∫sec2x(secx+tanx)92dx equals (for some arbitrary constant K). −1(secx+tanx)112{111−17(secx+tanx)2}+K 1(secx+tanx)111{111−17(secx+tanx)2}+K −1(secx+tanx)112{111+17(secx+tanx)2}+K 1(secx+tanx)112{111+17(secx+tanx)2}+K
View SolutionLet us consider the integral of the following forms
f(x1,√mx2+nx+p)1/2
Case I If m>0, then put √mx2+nx+C=u±x√m
Case II If p>0, then put √mx2+nx+C=ux±√p
Case III If quadratic equation mx2+nx+p=0 has real roots α and β there put √mx2+nx+p=(x−α)u or (x−β)u
∫(x+√1+x2)15√1+x2dx is equal to
View SolutionMatching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
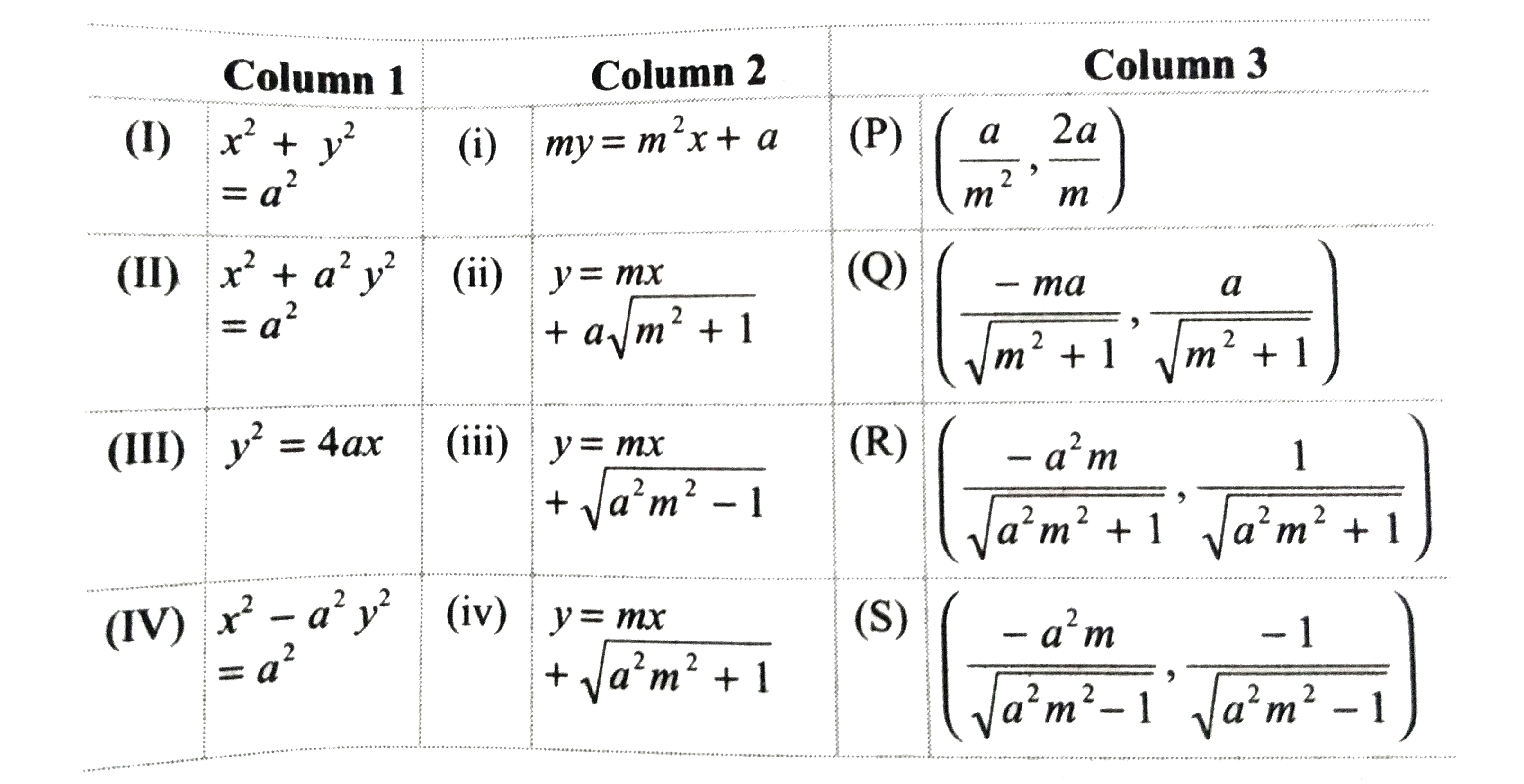
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View Solutionint((2x+3)dx)/(x(x+1)(x+2)(x+3)+1)=C-(1)/(f(x))
View Solutionint(e^(x))/(x^(4))dx=-(e^(x))/(3)[(1)/(x^(3))+(1)/(2x^(2))+(1)/(2x)]+(1)/(6)int(e^(x))/(x)dx
View SolutionIf ∫ex3+x2−1(3x4+2x3+2x)dx=f(x)+C, then the value of f(1)×f(−1) is−.
View SolutionIf ∫(2x+3)dxx(x+1)(x+2)(x+3)+1=C−1f(x) where f(x) is of the form of ax2+bx+c, then the value of f(1) is
View Solution∫3−x21−2x+x2exdx=exf(x)+c⇒f(x)=
View Solution∫e−xTan−1(ex)dx=f(x)−12log(1+e2x)+c⇒f(x)=
View SolutionLet f(x)=∫(4x4−2x3−3x2−4)dx(x4+x3+1)3/2. If f(0)=2, then the value of f(−1) is
View SolutionIf F(x)=∫(1+x)[(1−x+x2)(1+x+x2)+x2]1+2x+3x2+4x3+3x4+2x5+x6dx then find the value of [F(99)−F(3)]
View SolutionIf ∫e2xf1(x) dx = g (x), then ∫(e)2xf1(x)+e2xf(x)
View SolutionIf ∫ex3+x2−1(3x4+2x3+2x)dx=f(x)+C, then the value of f(1)×f(−1) is−.
View SolutionIf ∫(2x+3)dxx(x+1)(x+2)(x+3)+1=C−1f(x) where f(x) is of the form of ax2+bx+c, then the value of f(1) is
View Solution

