The relative density of a material is found by weighing the body first in air and then in water . If the weight in air is (10.0±0.1)gf and the weight in water is (5.0±0.1)gf, then the maximum permissible percentage error in relative density is
1
2
3
5
The correct Answer is:D
To find the maximum permissible percentage error in relative density, we will follow these steps:
Step 1: Understand the formula for Relative Density
Relative density (R) is defined as the ratio of the weight of a body in air (W_A) to its apparent loss of weight when submerged in water. The formula is given by:
R=WAWA−WW
where:
- WA = weight in air
- WW = weight in water
Step 2: Identify the values and their uncertainties
From the problem, we have:
- Weight in air, WA=10.0gf with an uncertainty of ΔWA=0.1gf
- Weight in water, WW=5.0gf with an uncertainty of ΔWW=0.1gf
Step 3: Calculate the apparent loss of weight
The apparent loss of weight when submerged in water is given by:
Apparent Loss in Weight=WA−WW=10.0gf−5.0gf=5.0gf
Step 4: Calculate the uncertainties in the quantities
The uncertainty in the apparent loss of weight (Y) can be calculated as:
ΔY=ΔWA+ΔWW=0.1gf+0.1gf=0.2gf
Step 5: Calculate the relative errors
Now, we can calculate the relative errors for WA and the apparent loss of weight:
- For WA:
ΔWAWA=0.110.0=0.01
- For the apparent loss of weight:
ΔYY=0.25.0=0.04
Step 6: Combine the relative errors
The total relative error in relative density can be expressed as:
ΔRR=ΔWAWA+ΔYY
Substituting the values:
ΔRR=0.01+0.04=0.05
Step 7: Convert to percentage error
To find the percentage error, we multiply by 100:
Percentage Error in R=0.05×100%=5%
Final Answer
The maximum permissible percentage error in relative density is 5%.
---
Relative density (R) is defined as the ratio of the weight of a body in air (W_A) to its apparent loss of weight when submerged in water. The formula is given by:
R=WAWA−WW
where:
- WA = weight in air
- WW = weight in water
From the problem, we have:
- Weight in air, WA=10.0gf with an uncertainty of ΔWA=0.1gf
- Weight in water, WW=5.0gf with an uncertainty of ΔWW=0.1gf
The apparent loss of weight when submerged in water is given by:
Apparent Loss in Weight=WA−WW=10.0gf−5.0gf=5.0gf
The uncertainty in the apparent loss of weight (Y) can be calculated as:
ΔY=ΔWA+ΔWW=0.1gf+0.1gf=0.2gf
Now, we can calculate the relative errors for WA and the apparent loss of weight:
- For WA:
ΔWAWA=0.110.0=0.01
ΔYY=0.25.0=0.04
The total relative error in relative density can be expressed as:
ΔRR=ΔWAWA+ΔYY
Substituting the values:
ΔRR=0.01+0.04=0.05
To find the percentage error, we multiply by 100:
Percentage Error in R=0.05×100%=5%
The maximum permissible percentage error in relative density is 5%.
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Multiple Correct
Explore 2 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Linked Comprehension
Explore 3 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Subjective
Explore 31 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
Dimensionsal methods provide three major advantages in verification , deviation , and changing the system of units . Any empirical formula that is derived based on this method has to be verified and propportionality constants found by experimental means . The presence or absence of certain factors - non dimensional constants or variables - cannot be identified by this method . So every dimensionally correct relation cannot be taken as perfectly correct.
The time period of oscillation of a drop depends on surface tension σ , density of the liquid ρ , and radius r . The relation is
View SolutionThe accuracy of measurement also lies in the way the results is expressed. The number of digits to which a value is to be expressed is one digit more than number of digits after after an operation is carried out on the given values. The error can be minimised by many trials and using the correct methods are instruments.
If the length and breadth are measured as 4.234and1.05m, the area of the rectangle is
View Solutionαt2=Fv+βx2
Find the dimension formula for [α]and[β] ( here t = time , F = force , v = velocity , x = distance).
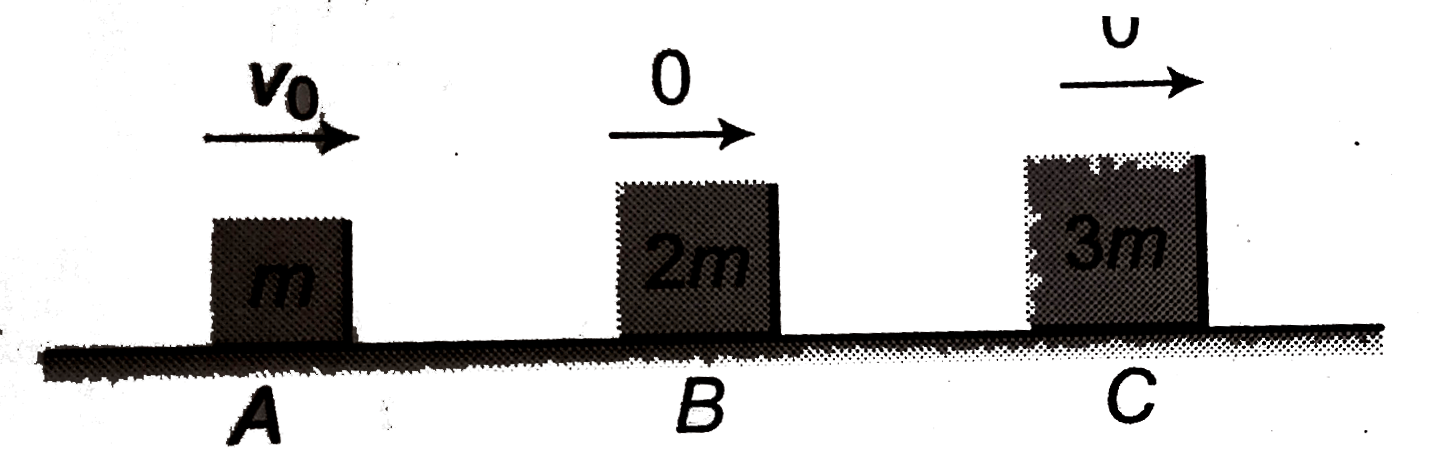
View SolutionThree objects A ,B and C are kept in a straight line on a smooth horizontal surface. These have masses m, 2m and 3m , respectively . The head - on elastic collision takes place between A and B and then B makes completely inelastic collision with C. All motions occur on the same straight line. The final speed of C will be
View SolutionA cyclindrical vessel of height 500 mm has an orifice (small hole) at its bottom. The orifice is initially closed any water is filled in ti upto height H.Now the top is completely sealed with a cap and the orifice at the bottom is opened .Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. The fall in height (in mm) of water level due to opening of the orifice is [ Take atmospheric pressure = 1.0×105Nm2, density of water = 1000kgm3. Neglect any effect of surface tension.]
View SolutionThe relative density of material of a body is found by weighting it first in air and then in water . If the weight in air is ( 5.00 +- 0.05) N and the weight in water is (4.00 +- 0.05) N . Find the relative density along with the maximum permissible percentage error.
View SolutionThe relative density of a material of a body is found by weighing it first in air and then in water. If the weight of he body in air is W_(1) = 8.00 +- N and the weight in water is W_(2) = 6.00 +- 0.05 N , then the relative density rho_(r ) = W_(1)//( W_(1) - W_(2)) with the maximum permissible eror is
View SolutionThe relative density of a material is found by weighing the body first in air and then in water . If the weight in air is (10.0±0.1)gf and the weight in water is (5.0±0.1)gf, then the maximum permissible percentage error in relative density is
View SolutionThe relative density of a material is found by weighing the body first in air and then in water. If the weight in air is (20.0±0.1)N and weight and water is (10.0±0.1)N, what would be the maximum percentage error in relative density?
View SolutionThe relative density of a material is found by weighing the body first in air and then in water. If the weight in air is (10.0±.01)N and weight and water is (5.0±0.1)N, what would be the maximum percentage error in relative density?
View SolutionThe relative density of the material of body is the ratio of it's weight in air and to the apparent loss of it's weight in water. By using a spring balance. The weight of body measured in air is (5.00+0.05) N. The weight of the body measured in water is found to be (4.00±0.05) N. Then the maximum possible percentage error in relative density is
View SolutionThe relative density of material of a body is found by weighting it first in air and then in water . If the weight in air is (5.00±0.05)N and the weight in water is (4.00±0.05)N. Find the relative density along with the maximum permissible percentage error.
View SolutionA body weighs 200 gf in air and 190 gf when completely immersed in water. Calculate:
(i) the loss in weight of the body in water.
(ii) the upthrust on the body.
View SolutionA body weighs 82.1 gf in air, 75.5 gf in water and 73.8 gf in a liquid. A. Find the relative density of the liquid. B. How much will it weigh if immersed in a liquid of relative density 0.87 ?
View SolutionA body weighs W gf in air and W_(1) gf when it is completely immersed in water. Find (i) volume of the body (ii) upthrust on the body. (iii) relative density of material of the body.
View Solution
