A ball (A) is thrown straight up from the edge of the roof of a building. Another ball (B) is dropped from the roof 1.00s later. You may ignore air resistance . (a) If the height of the building is 20.0m, what must the initial speed of ball A be if both are to hit the ground at the same time? (b) On the same graph sketch the position and velocity of each balls a function of time, measured from when the first ball is thrown and taken origin at ground.
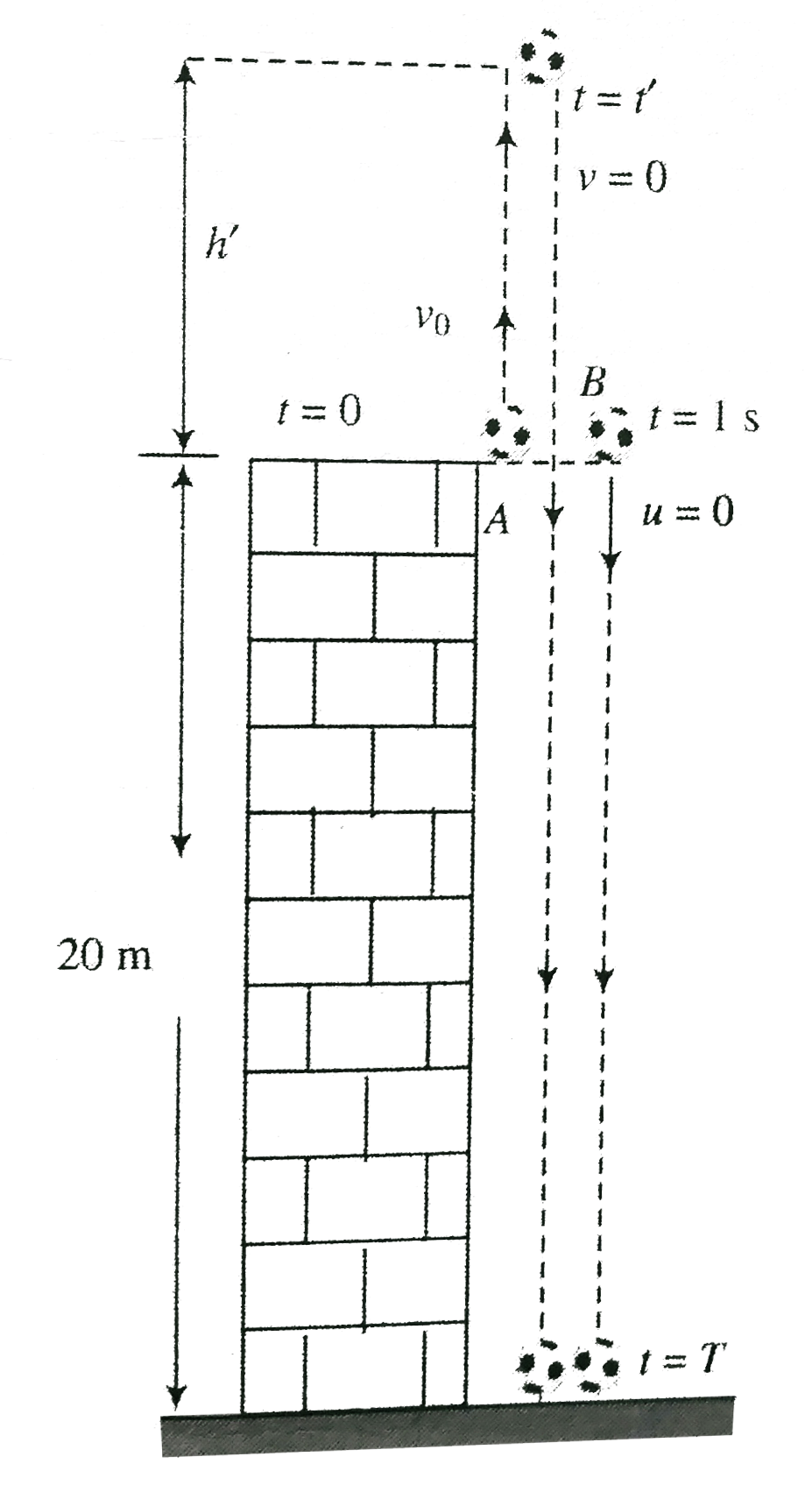 .
.
For the purpose of doing all four farts with the least reperition of algebra, quantities will be dented symbolically. That is, let
y1=h+v0t−12gt1 and y2=h−12g(t−t0)2.
In this case, t0=1.00s. Setting y1=y2=0, expanding the binomial (t−t0)2, which can be solved for t,
t=12gt20gt0−v0=t021(1−v0gt0) Substiuting this into the expressinon for y1 and setting y1=0 and solving for h as a function of v0 yields after some algebra,
h=12gt20(12gt0−v0)2(gt0−v0)2
a. Using the given value, t0=1.00s and g=9.80ms−2.
h=20.0m=(4.9m)(4.9ms−1−v09.8ms−2−v0)
This has two solutions, one of which is not physical [the first ball is still going up when the second is released, see part C]. The physical solution invlves taking the negative square root before solving for v0, and yields 8.2ms−1
 .
.
b. The above expression gives
for (i) 0.411m and for (ii) 1.15km.
C. As v0 approaches 9.8ms−1, the height h becomes infinite corresponding to a relative velocity at the second ball is throun that approaches zero, If v0≤9.8ms−1, the first ball can never catch the second ball.
d. As v0 approaches 4.9ms−1 the height approaches zero. This corresponds to the first ball being closer and is released. If v0≤4.9ms−1, the first ball will already have roof on the wau down nefore the second ball is released, and the second ball can catch up.
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Exercise 4.3
Explore 14 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Exercise 4.4
Explore 15 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Exercise 4.1
Explore 17 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
A ball is thrown vertically upward with a speed of 20 m/s. Draw a graph showing the velocity of the ball as a function of time as it goes up and then comes back.
View SolutionThe ball is dropped from a bridge 122.5m above a river, After the ball has been falling for 2 s, a second ball is thrown straight down after it. What must its initial velocity be so that both hit the water at the same time ?
View Solution
Knowledge Check
A ball A is thrown up vertically with a speed u and at the same instant another ball B is released from a height h. At time t, the speed A relative to B is
AuBu - 2gtC√u2−2ghDu - gt
A ball dropped from the top of a building takes 0.5 sec to clear the window of 4.9 m height. What is the height of building above the window?
View SolutionA ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View SolutionA ball is dropped from the top of a building the ball takes 0.5 s to fall past the 3 m length of a window at certain distance from the top of the building. Speed of the ball as it crosses the top edge of the window is (g=10m/s2)
View SolutionA ball is dropped from the top of a building. The ball takes 0.5s to fall the 3m length of a window some distance from the to of the building. If the speed of the ball at the top and at the bottom of the window are vT and vT respectively, then (g=9.8m/s2)
View SolutionA ball A is projected from the ground such that its horizontal range is maximum. Another ball B is dropped from a height equal to the maximum range of A. The ratio of the time of flight of A to the time of fall of B is
View SolutionA person standing near the edge of the top of a building throws two balls A and B. The ball A is thrown vertically upward and B is thrown vertically downward with the same speed. The ball A hits the ground with speed vA and the ball B hits the ground wiht a speed vB. We have
View SolutionA ball is dropped from the top of a tower of height 78.4 m Another ball is thrown down with a certain velocity 2 sec later. If both the balls reach the ground simultaneously, the velocity of the second ball is
View Solution
