Find the average acceleration in first 20s. (Hint: Area under a−t graph is equal to the change in velocity).
 .
.
Let us first find the charge in velocity Change in velcity is the area under the acceleration=time graph. For first 20s,
Area =Δv12×10×20+10×20=300ms−1
Average acceleration =ΔvΔt=30020=15ms−2.
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Subjective
Explore 29 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Single Correct
Explore 52 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Exercise 4.3
Explore 14 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
Statement-I : When velocity of a particle is zero then acceleration of particle is zero.
Statement-II : Acceleration is equal to rate of change of velocity.
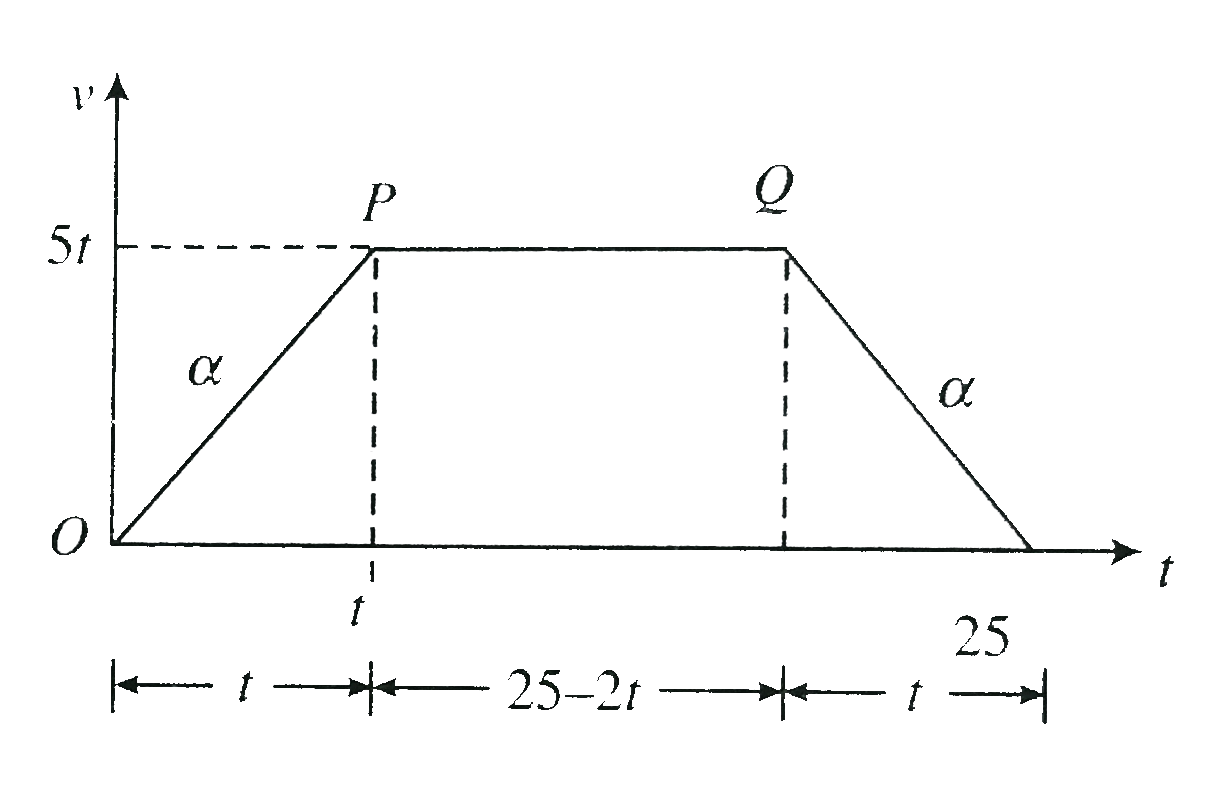
View SolutionThe velocity-time graph of a particle moving along a straight line is shown is Fing. The rate of acceleration and deceleration is constant and it is equal to 5ms−2. If the a average velocity during the motion is 20ms−1, Then
 .
.
The distace travelled with uniform velcoty is .
View Solution
Knowledge Check
The area under acceleration-time graph gives
Aintial velocityBfinal velocityCchange in velocityDdistance travelled
The area under acceleration-time graph gives
View SolutionThe velocity-time graph of a particle moving along a straight line is shown is . The rate of acceleration and deceleration is constant and it is equal to 5ms−2. If the a average velocity during the motion is 20ms−1, Then
 .
.
The value of t is.
View SolutionThe velocity-time graph of a particle moving along a straight line is shown is Fig. The rate of acceleration and deceleration is constant and it is equal to 5ms−2. If the a average velocity during the motion is 20ms−1, Then
 .
.
The maximum velocity of the particle is .
View SolutionThe velocity-time graph of a particle moving along a straight line is shown is Fig. The rate of acceleration and deceleration is constant and it is equal to 5ms−2. If the a average velocity during the motion is 20ms−1, Then
 .
.
The maximum velocity of the particle is .
View Solutionvelocity-time graph of a particle moving in a straight line is as shown in figure. At time t=0, velocity of the particle is zero. Find
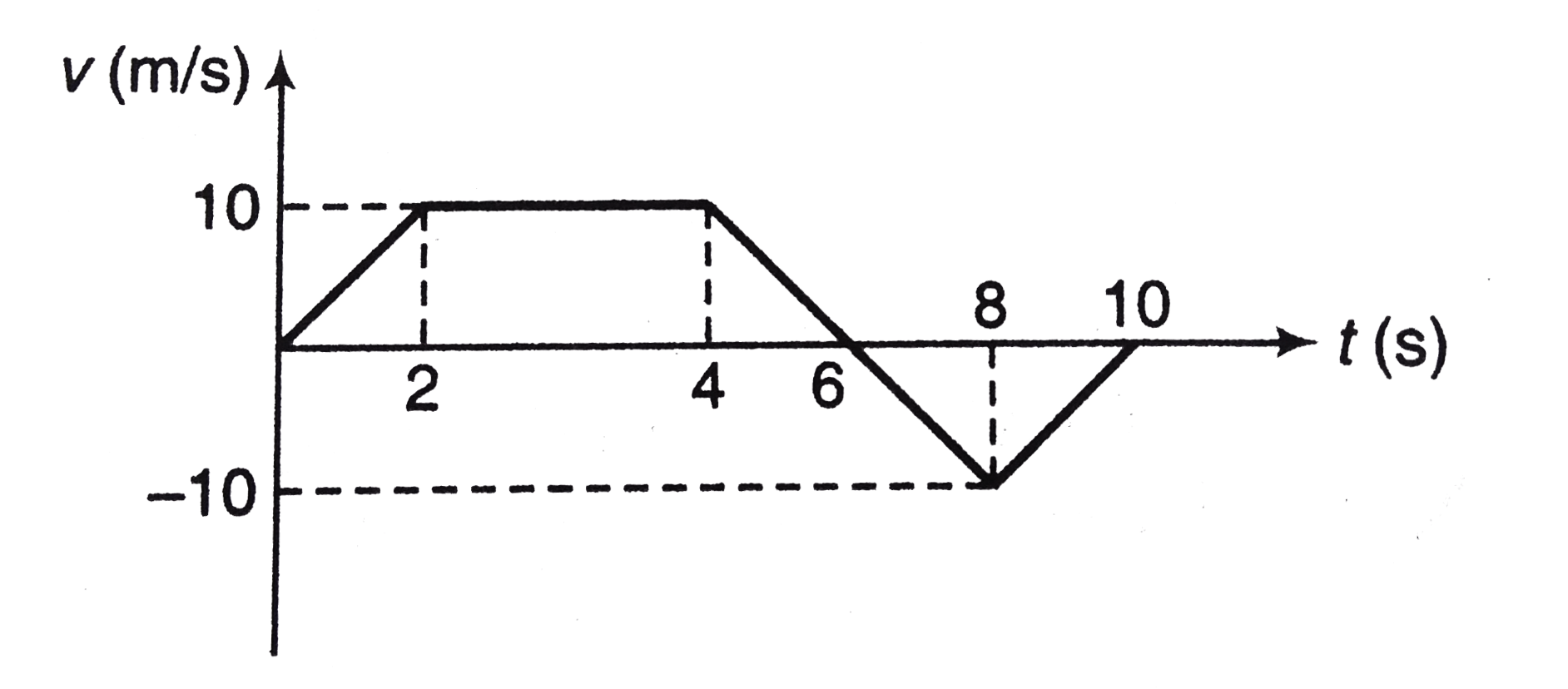
(a) average acceleration in a time interval from t=6s to t=12s,
(b) velocity of the particle at t=14s.
View SolutionAssertion : In the s-t graph as shown in figure, velocity of particle is negative and acceleration is positive.
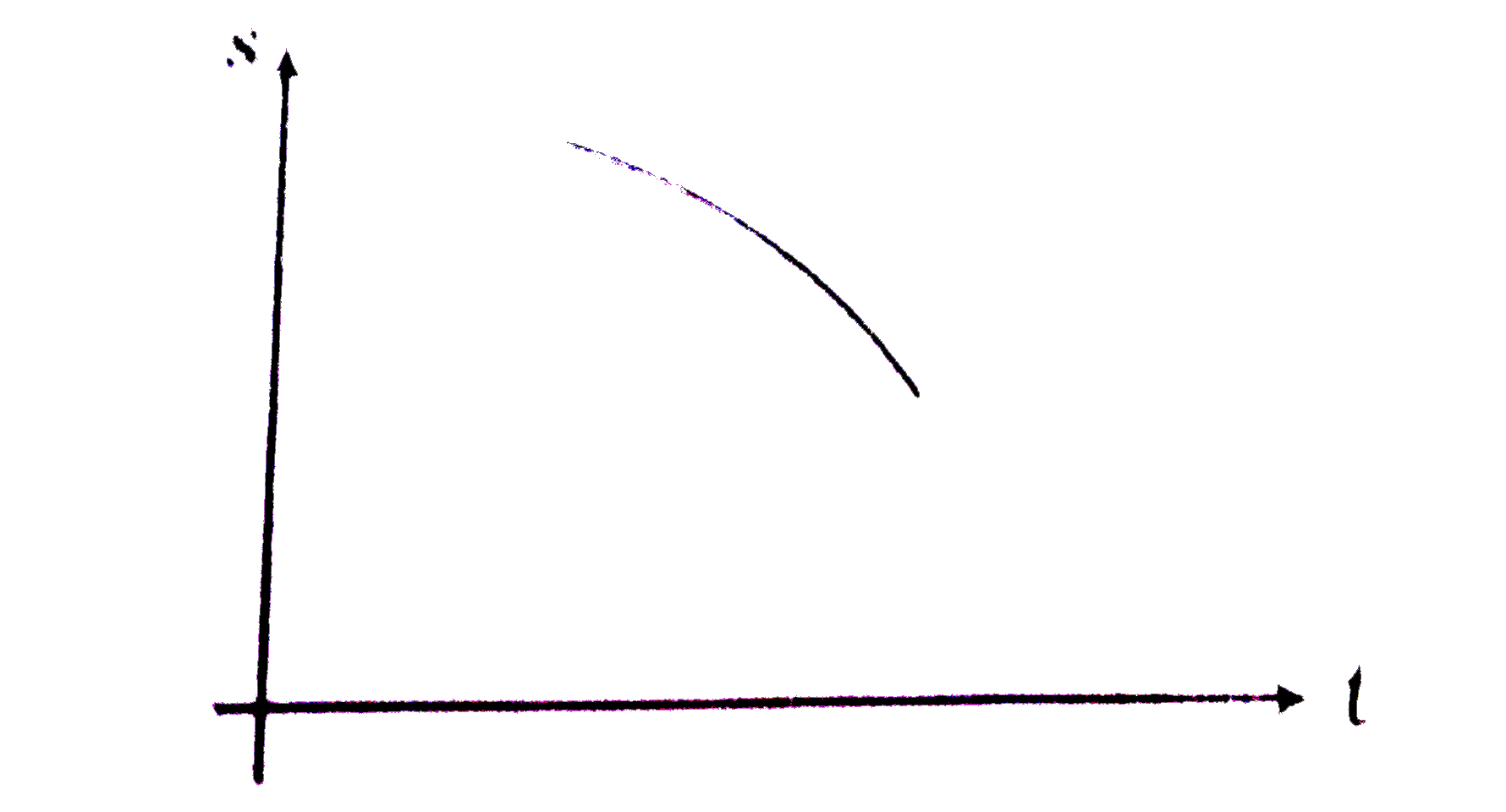
Reason : Slope of s-t graph is negative and increasing in magnitude.
View SolutionFor Question , find maximum velocity and maximum acceleration
Hint : Maximum velocity =Aω
Maximum acceleration=Aω2
A particle executes SHM on a straight line path. The amplitude of oscillation is 3cm . magnitude of its acceleration is equal to that of its velocity when its displacement from the mean position is 1cm.
View Solution
