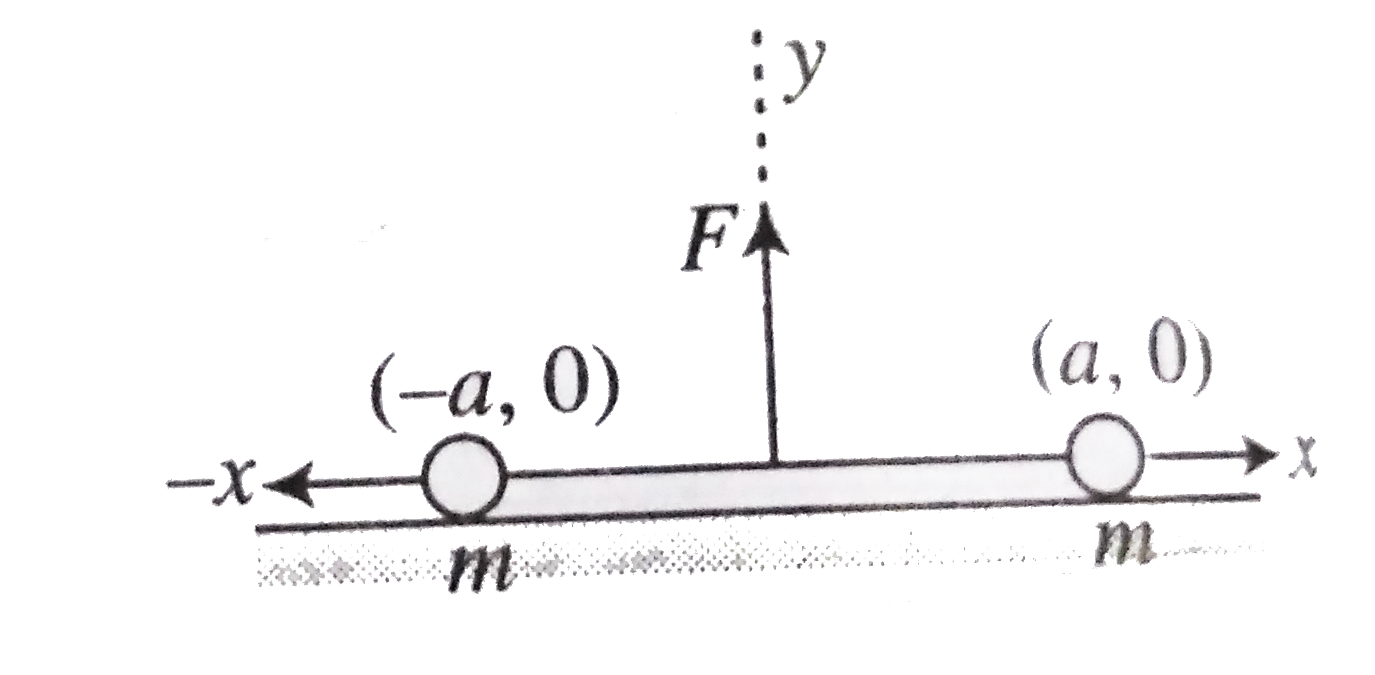
Two masses each equal to m are lying on x-axis at (−a,0)(+a,0) respectively as shown in figure They are connected by a light string A force F is applied at the origin along vertical direction As a result the masses move toward each other without loosing contact with ground What is the acceleration of each mass? Assume the instantanceous position of the masses as(−x,0)and (x,0)
a. 2Fm√a2−x2x
b. 2Fm.x√a2−x2
c, F2m.x√a2−x2
d. Fmx√a2−x2
The correct Answer is:c
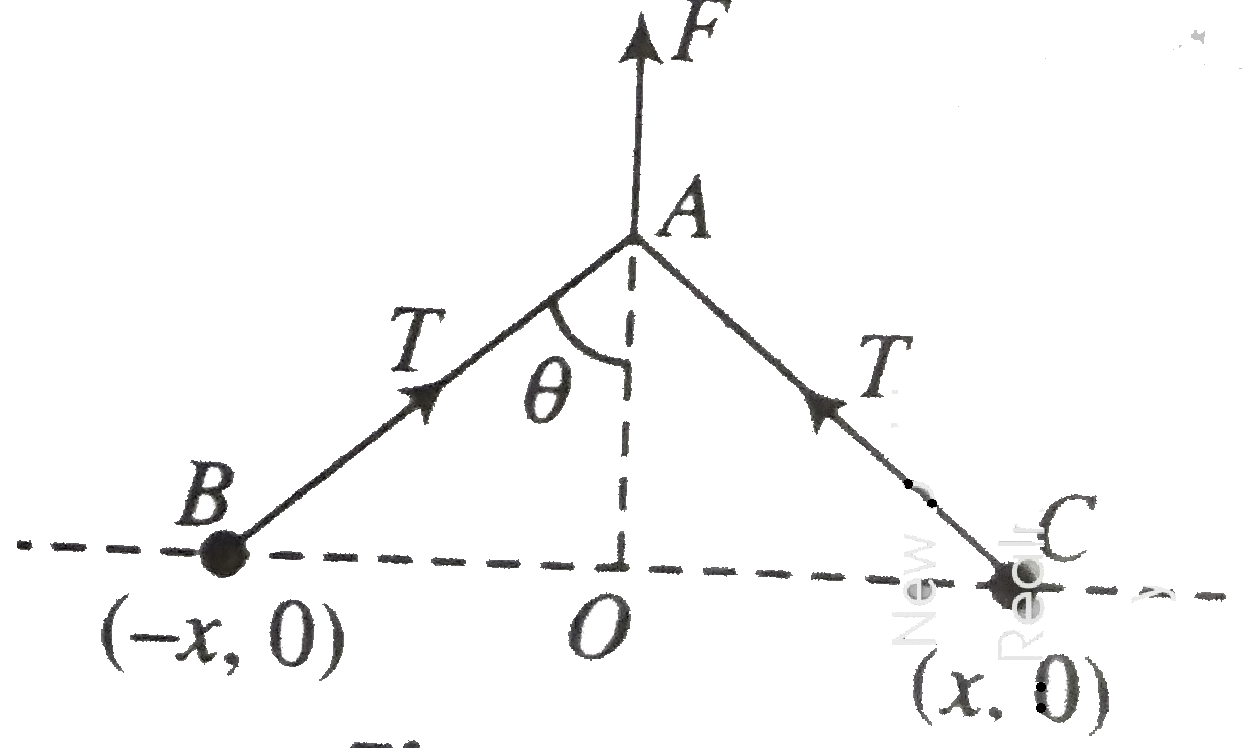
From figure F=2Tcosθ
T=F/2cosθ
The force responsible for motion of masses m x-axis is Tsinθ
ma=Tsinθ=F2sinθ×sinθ
=F2tanθ=F2×OBOA=F2×x√(a2−x2)
So a=F2m=x√a2−x2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Multiple correct answer type
Explore 3 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Assertion -reasoning
Explore 2 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:True And False
Explore 4 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
Two masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is

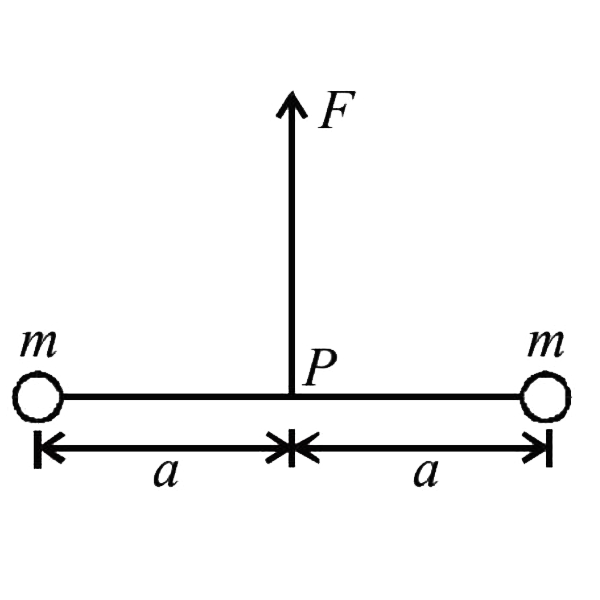
View SolutionTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
View Solution
Knowledge Check
Two identical small masses each of mass m are connected by a light inextensible string on a smooth horizontal floor. A constant force F is applied at the mid point of the string as shown in fig. find the acceleration of each mass towards each other.
 AF2ma√a2−x2BF2m−x√a2−x2CF2mxaDF2m√a2−x2x
AF2ma√a2−x2BF2m−x√a2−x2CF2mxaDF2m√a2−x2x
Three blocks with masses m , 2m and 3m are connected by strings, as shown in the figure. After an upward force F is applied on block m , the masses move upward at costant speed v . What is the net force on the block of mass 2m ? (g is the acceleration due to gravity). ltBrgt

View SolutionThree blocks with masses m , 2m and 3m are connected by strings, as shown in the figure. After an upward force F is applied on block m , the masses move upward at costant speed v . What is the net force on the block of mass 2m ? (g is the acceleration due to gravity). ltBrgt

View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
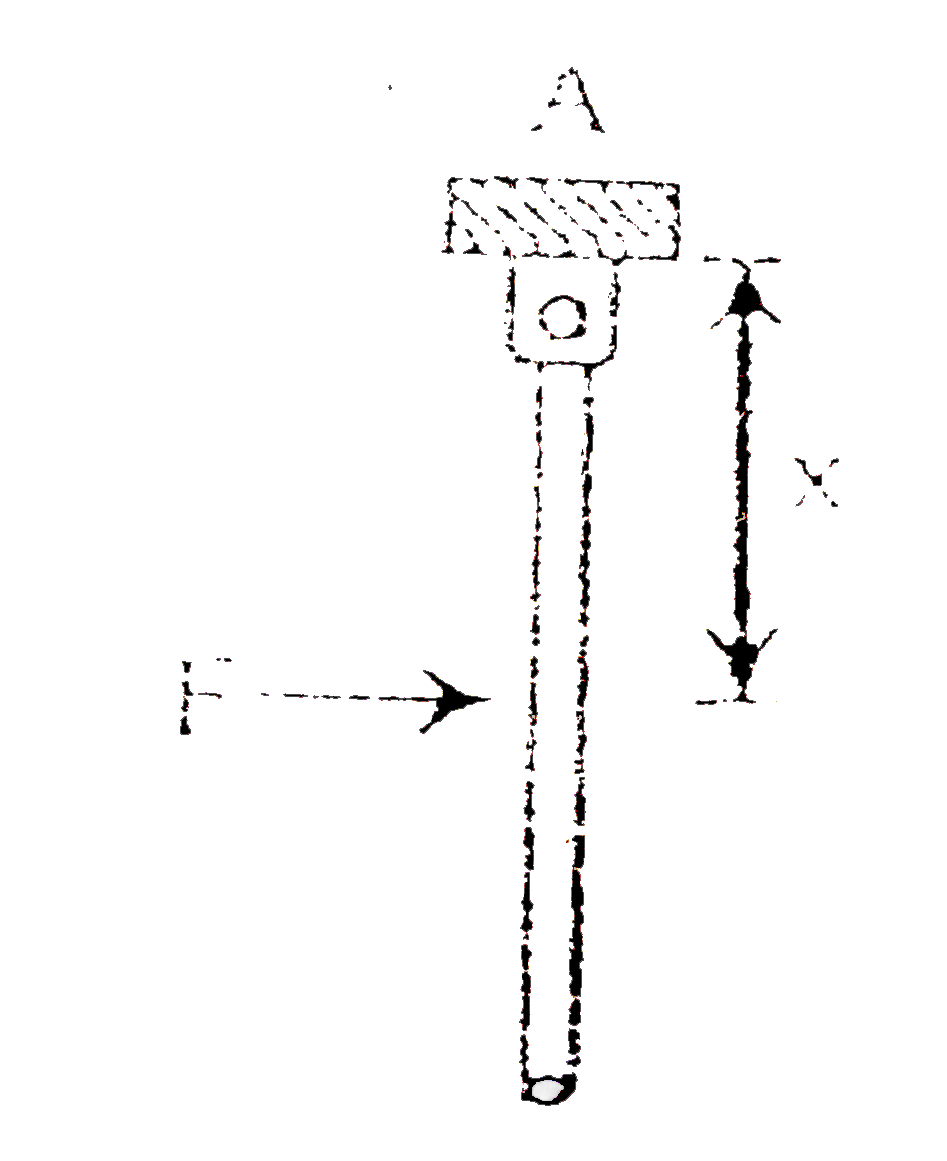
View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
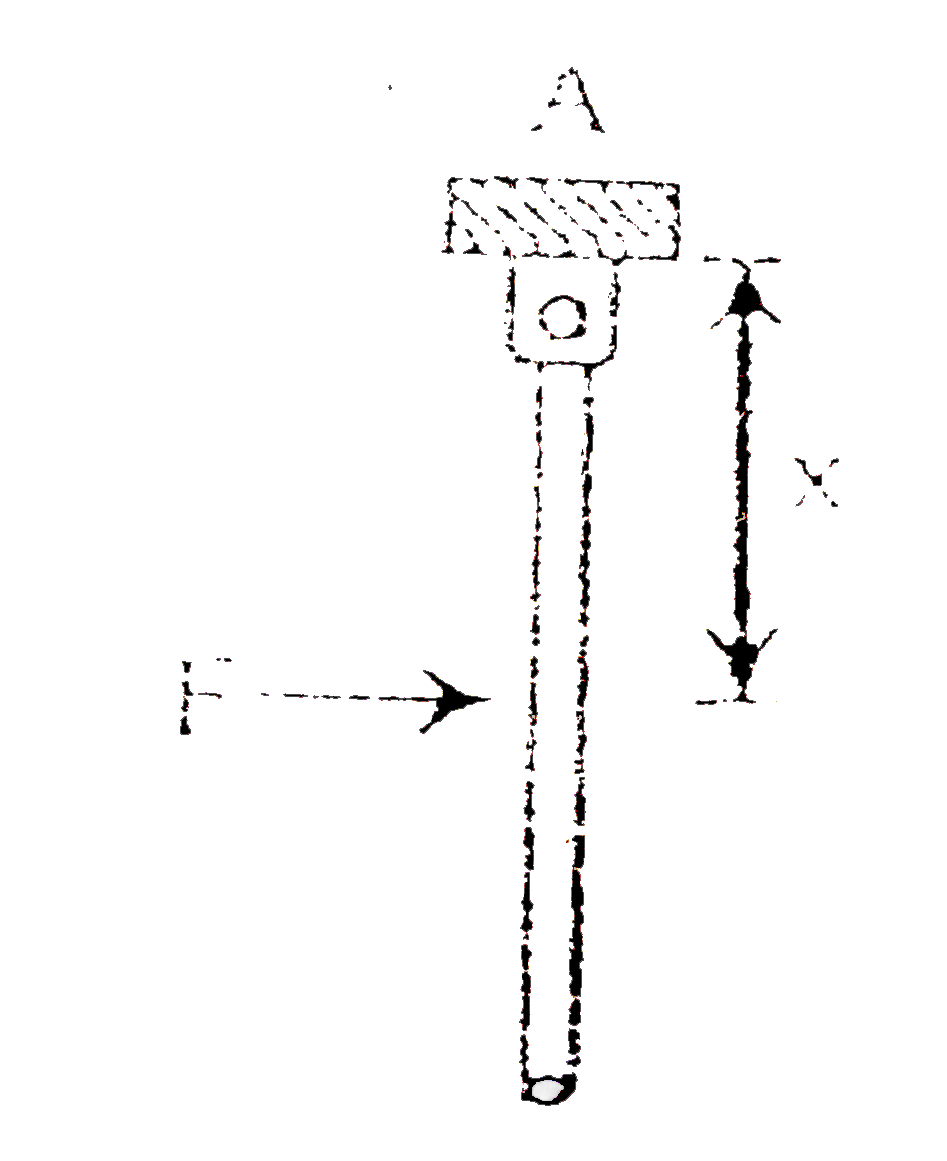
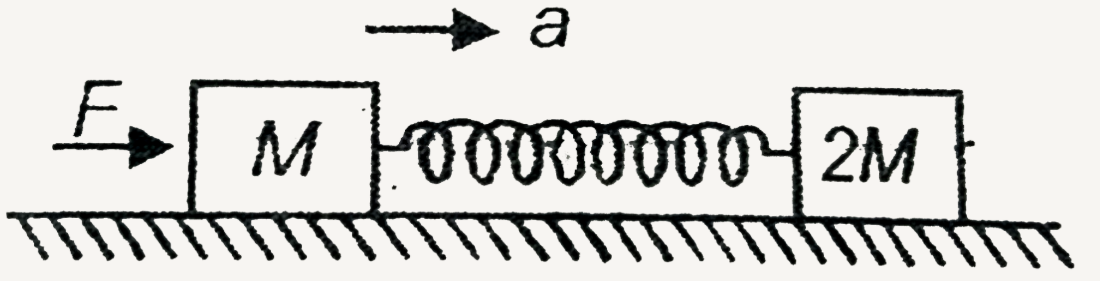
View SolutionTwo blocks of masses M and 2M are connected to each other through a light spring as shown in figure . If we push the mass M with a force F which cause acceleration a in mass M. what will the acceleration in 2M?
View SolutionTwo charges, each equal to q, aer kept at x=−a and x=a on the x-axis. A particle of mass m and charge q0=q2 is placed at the origin. If charge q0 is given a small displacement (ylt lt a) along the y-axis, the net force acting on the particle is proportional to
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as

View Solution
