A point mass m connected to one end of inextensible string of length l and other end of string is fixed at peg. String is free to rotate in vertical plane. Find the minimum velocity given to the mass in horizontal direction so that it hits the peg in its subsequent motion.
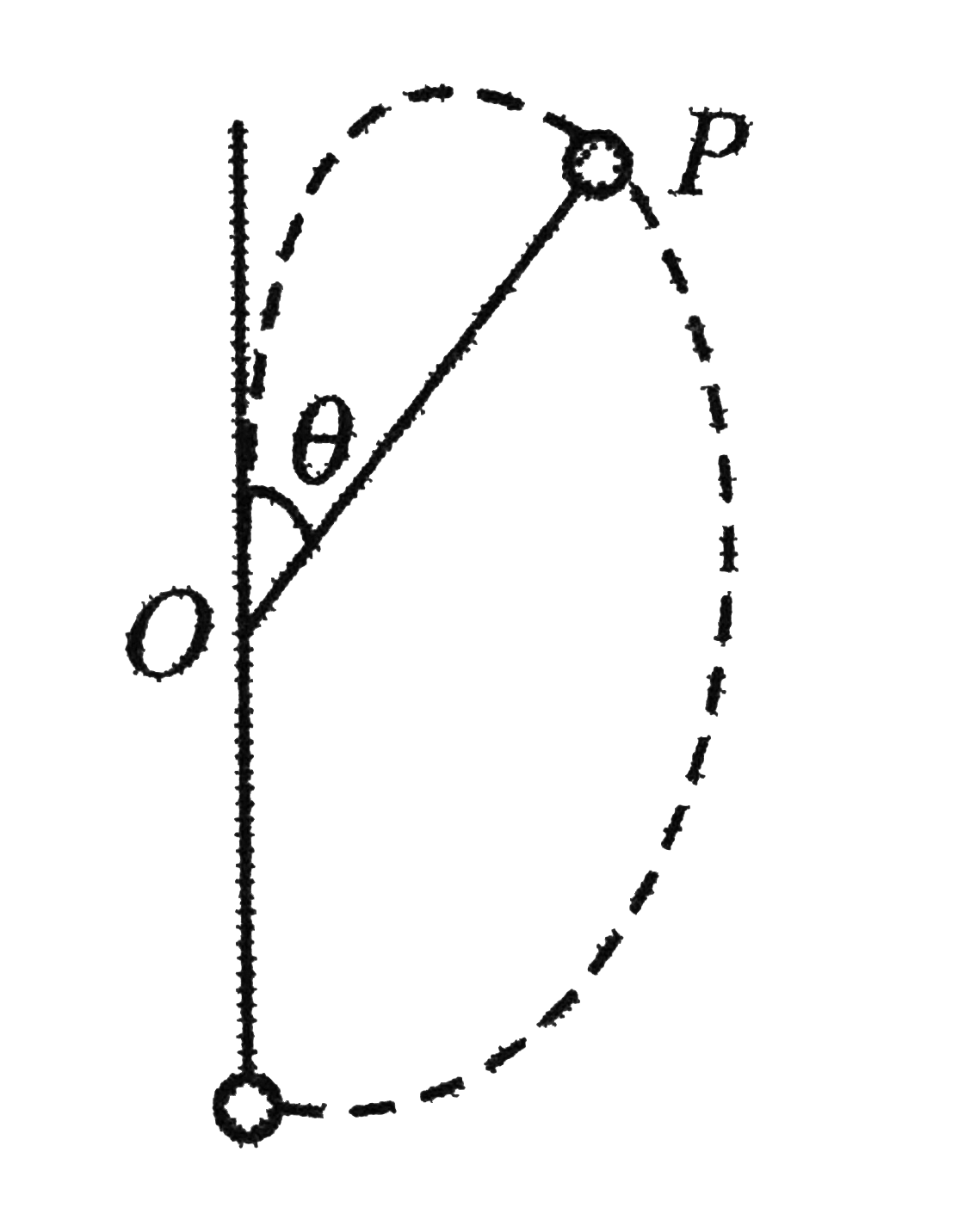
Tension in string is zero at point P in its subsequent motion, after this point its motion is projectile. Velocity at point P, T=0.
⇒mgcosθ=mv2lv=√glcosθ
Assume its projectile motion start at point P and it passes through point C. So that equation of trajectory satisfy the co-ordinate of C(lsinθ,−lcosθ)

Equation of trajectory,
y=xtanθ−gx22v2cos2θ
=(lsinθ)tanθ−g(lsinθ)22(glcosθ)cos2θ
=−cosθ=sin2θcosθ−12sin2θ2cos3θ
⇒−2cos4θ=2sin2θcos2θ−sin2θ
⇒sin2θ=2sin2θcos2θ+2cos4θ
=2cos2θ(sin2θ+cos2θ)
⇒tan2θ=2
⇒tanθ=√2 hence, cosθ=1√3, sinθ=√23
From energy conservation between point P and A,
12mu2=12mv2+mg(1+cosθ)
⇒u2=v2+2gl(1+cosθ)
=2gl+3glcosθ=2gl+3gl1√3
⇒u=[(2+√3)gl]1/2
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Solved Examples
Explore 15 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
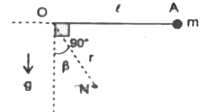
A point mass m is connected with ideal inextensible string of length l and other end of string is tied at point O as shown in the figure. The string is made horizontal and mass is released from point A to perform vertical circular motion. There is a nail at point N such that ON =r . Find the value of r so that mass m is able to just perform complete vertical circular motion about point N.
View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
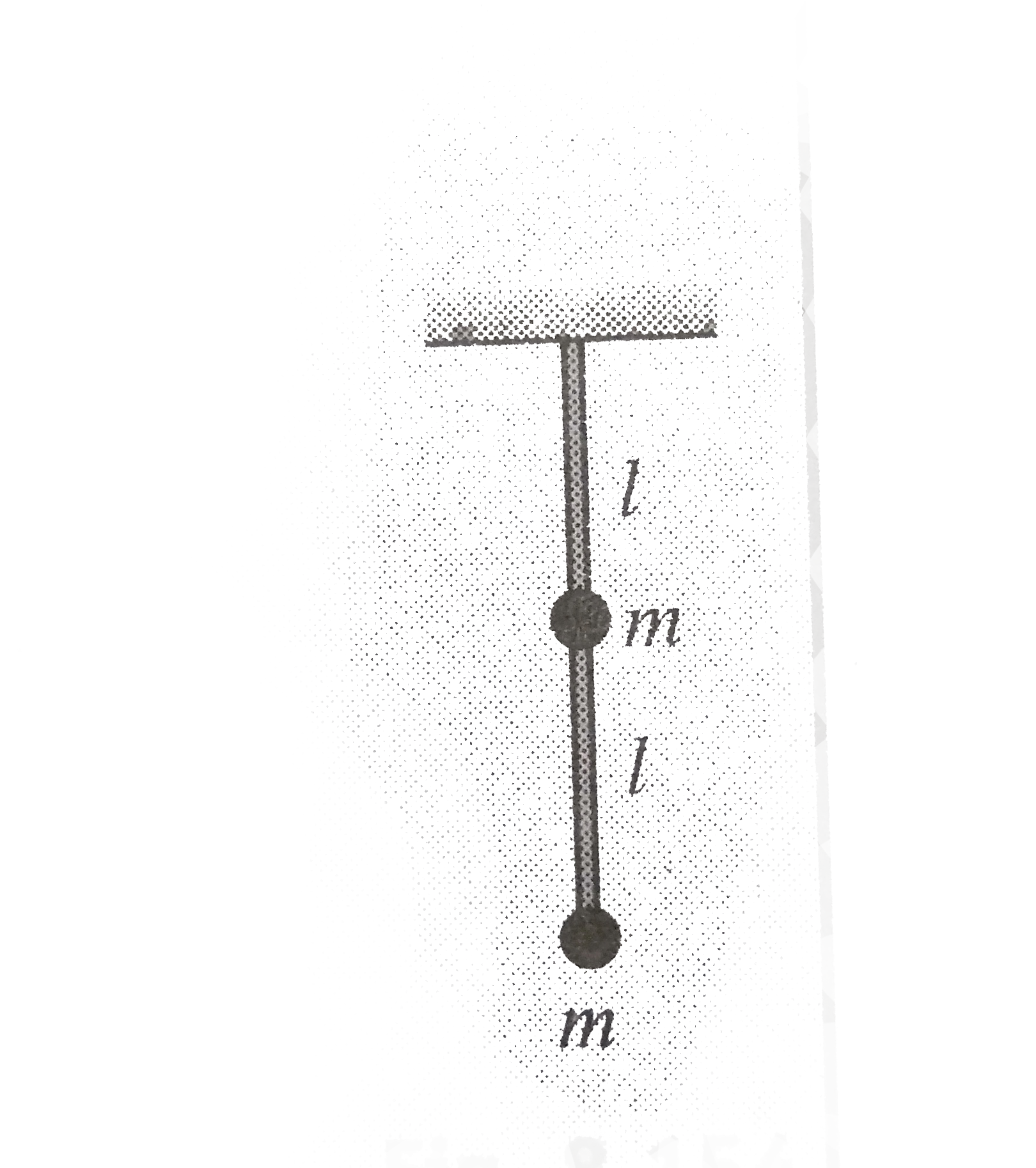
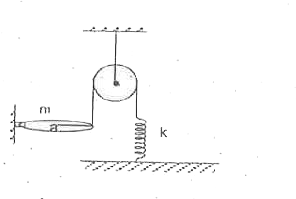
View SolutionA ring of mass m and radius a is connected to an inextensible string which passes over a frictionless pulley. The other end of string is connected to upper end of a massless spring of spring constant k. The lower end of the spring is fixed. The ring can rotate in the vertical plane about hinge without any friction. If horizontal position of ring is equilibrium position then find time period of small in oscillations of the ring.
View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical is
View SolutionA ball of mass m is attached to a string whose other end is fixed. The system is free to rotate in vertical plane. When the ball swings, no work is done on the ball by the tension in the string. Which of the following statement is the correct explanation?
View SolutionA particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then

View SolutionA particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then

View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
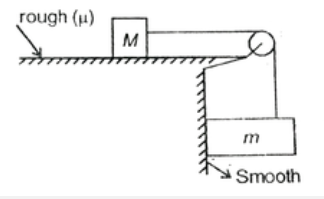
The minimum value of coefficient of friction μ such that system remains at rest , is
View SolutionOne end of a light rod of length 1m is attached with a string of length 1m. Other end of the rod is attached at point O such that rod can move in a vertical circle. Other end of the string is attached with a block of mass 2kg. The minimum velocity that must be given to the block in horizontal direction so that it can complete the vertical is (g=10m/s2)
View Solution
