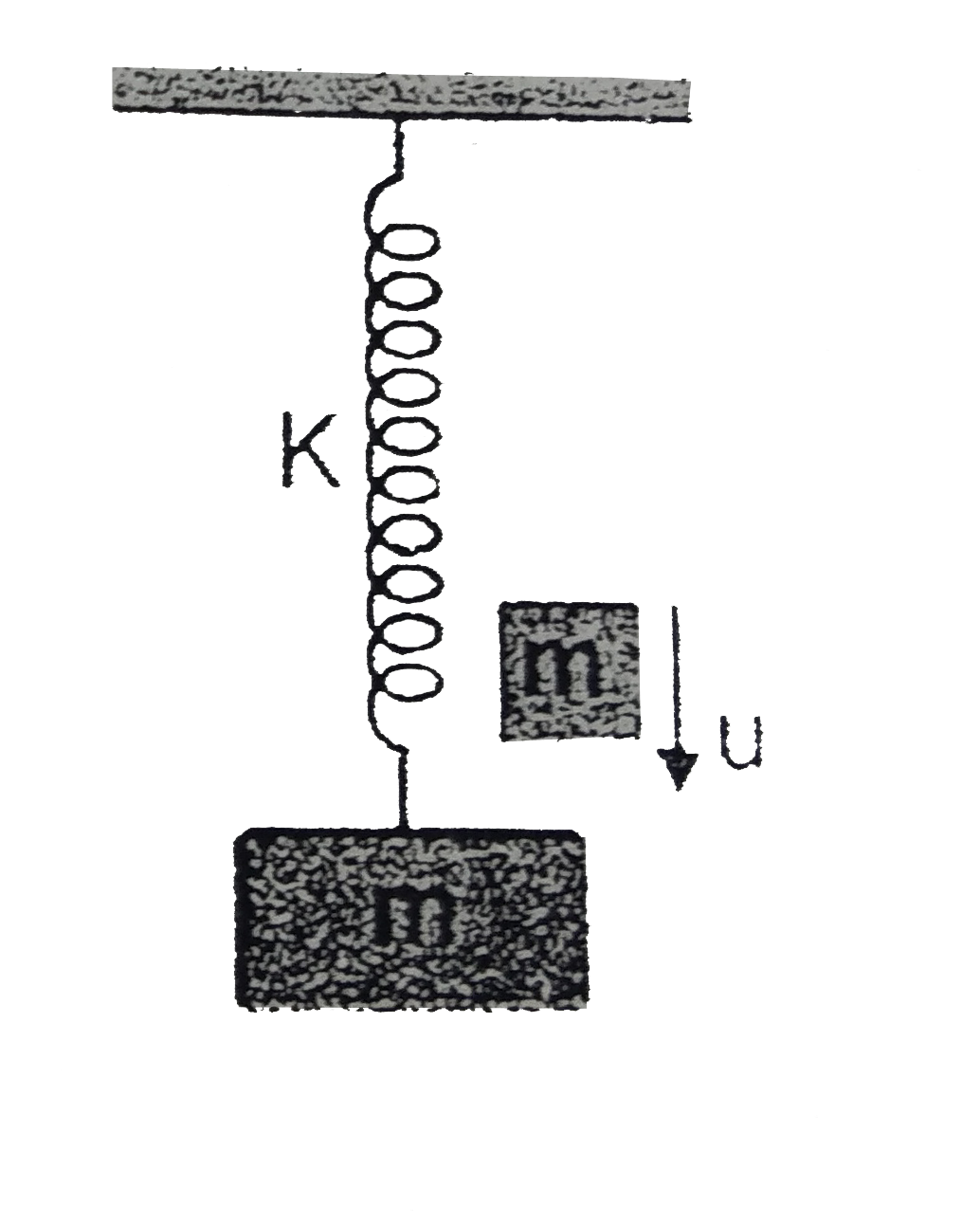
Block A is hanging from vertical spring of spring constant K and is rest. Block B strikes block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is
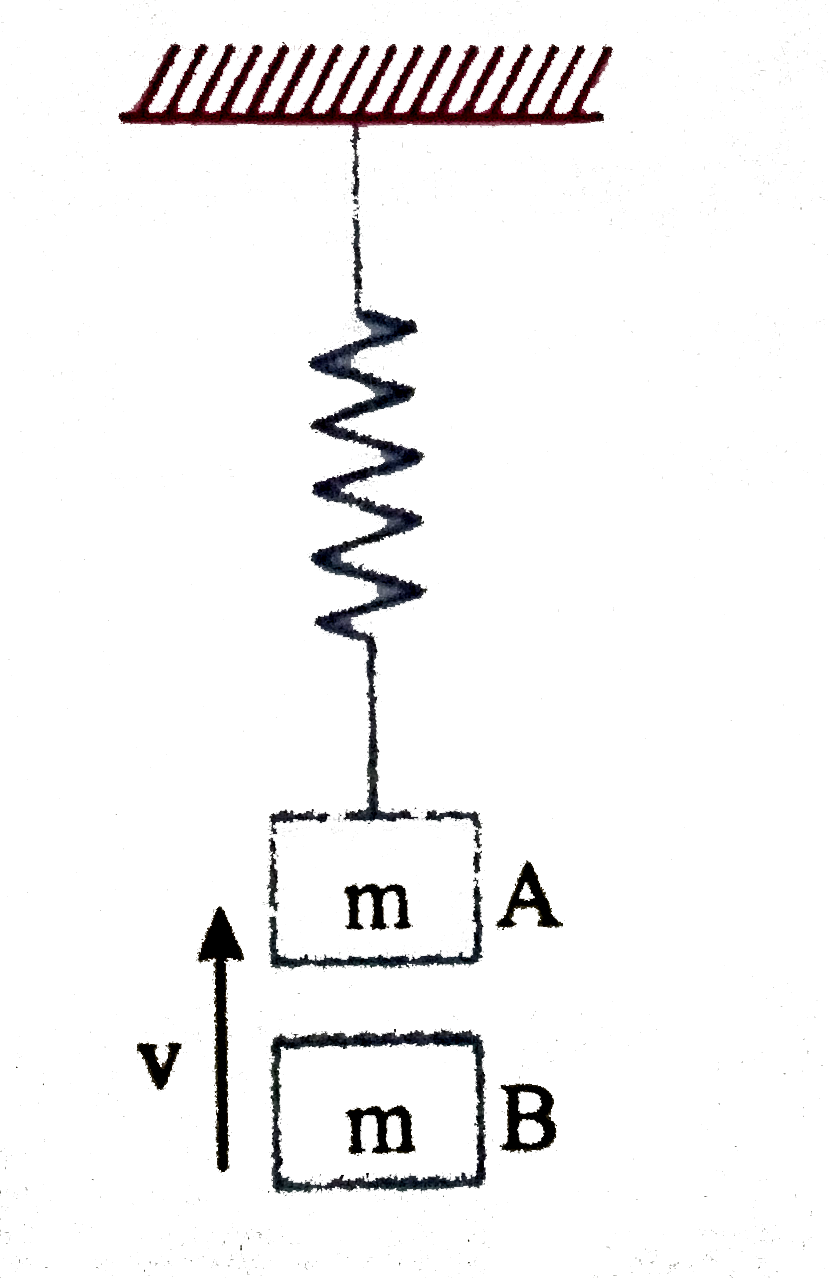
(a) √60mg2k
(b) √6mg2k
(c) √10mg2k
(d) None of the above
The correct Answer is:B
The initial extension in spring is x0=mg/k
Just after collision of B with A, the speed of the combined mass is v/2. For the spring to just attain natural length, the combined mass must rise up by x0=mg/k and come to rest.

Applying conservation of energy between initial and final states,
122m(v2)2+12k(mgk)2=2mg(mgk)
Solving, we get v=√6mg2k
टॉपर्स ने हल किए ये सवाल
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
समान प्रश्न
Block A is hanging from a vertical spring and is at rest. Block B strikes the block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is

View SolutionBlock A is hanging from a vertical spring and is at rest. Block B strikes the block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is

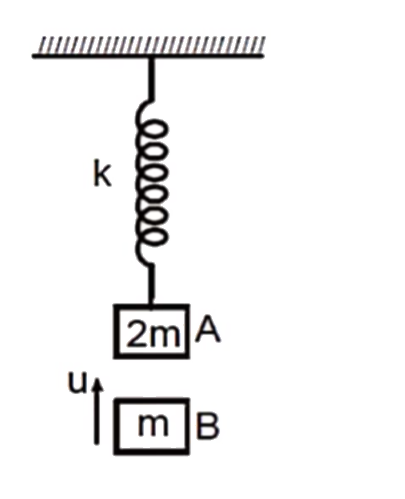
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
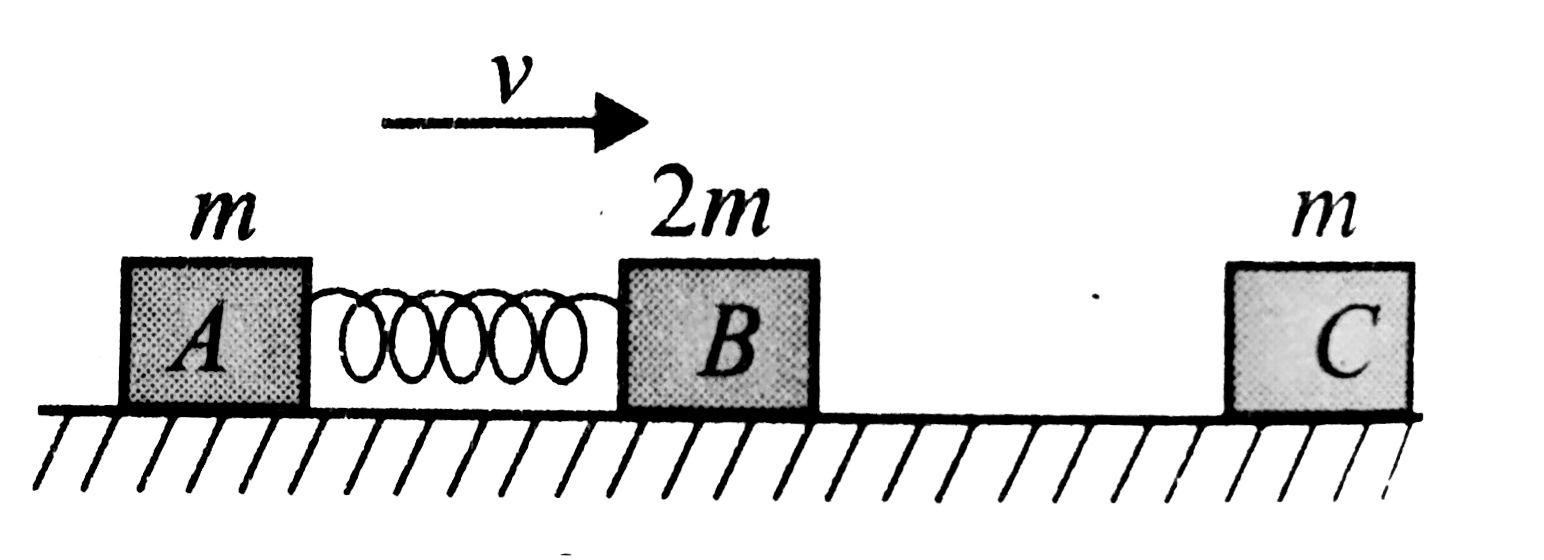
View SolutionTwo blocks A and B of masses in and 2m, respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1/2. The maximum compression in the spring is
View SolutionA block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
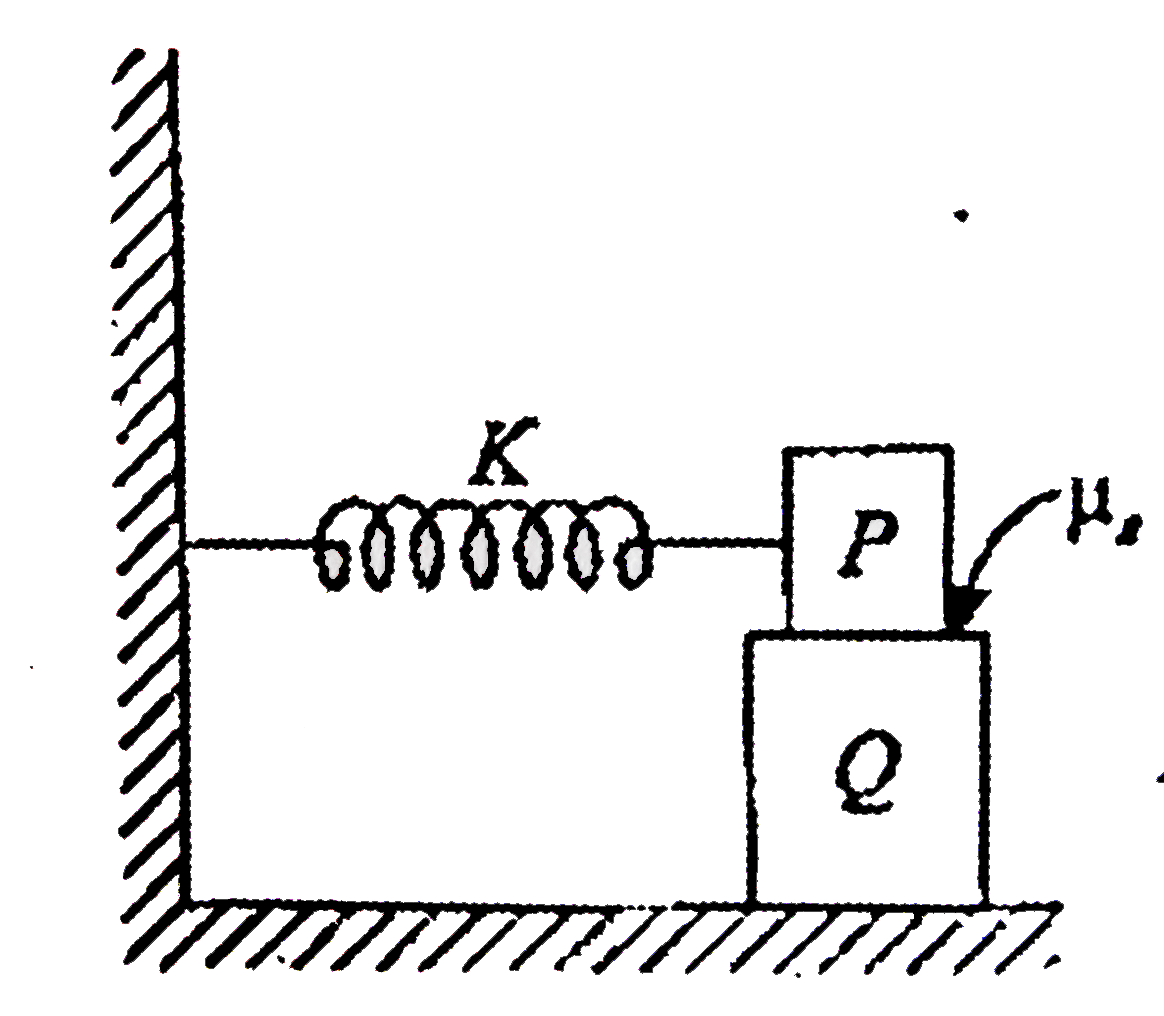
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionTwo block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.

The velocity of block B just after collision is -
View SolutionConsider a block of mass 'm' attached to a spring of spring constant 'K' as shown. Now a block of same mass 'm' moving with velocity 'u' strikes the other block and stick to it. Both blocks collectively start performing SHM.
Choose the correct option(s) :
View Solution

