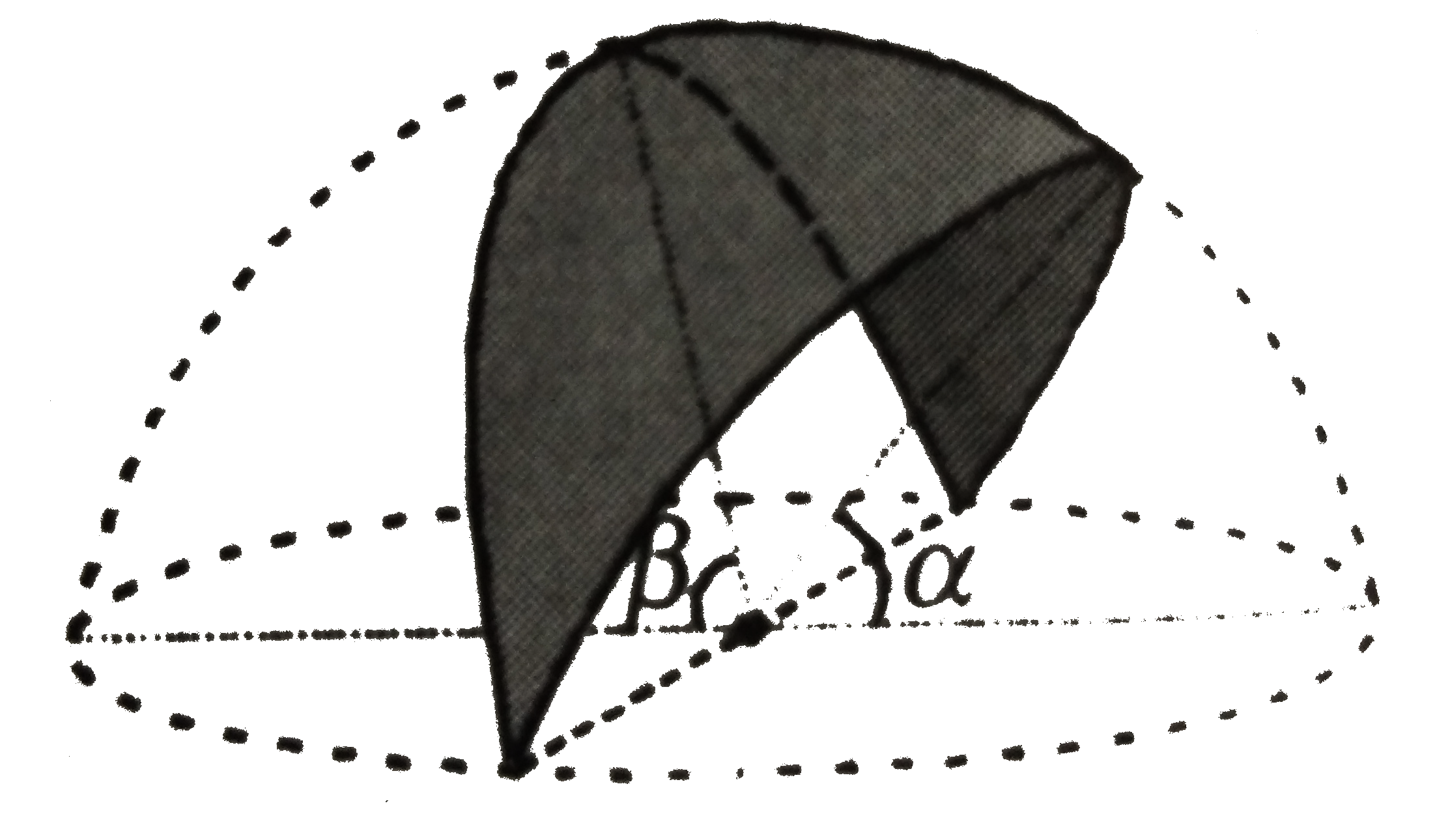
The electric field intensity at the center of a uniformly charged hemispherical shell is E0. Now two portions of the hemisphere are cut from either side, and the remaining portion is shown in fig. If α=β=π/3, then the electric field intesity at the center due to the remaining portion is
E0/3
E0/6
E0/2
information insufficient
The magnitude of electric field intensity due to each part of the hemisherical surface at the center 'O' is same. Suppose it is E.

E=E2+E2=E0
or, 2E=E0
or E=E02.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Comprehension
Explore 25 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Subjective
Explore 32 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:single correct type
Explore 14 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
Similar Questions
Knowledge Check
Electric field intensity (E) due to an electric dipole varies with distance (r ) from the point of the center of dipole as :
A1rand1r2B1r2and1rC1r3and1r3D1r3and1r2
The electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionTwo charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
View Solution
A small part of dl length is removed from a ring having charge per unit length λ. Find electric field at centre due to remaining ring.
View SolutionFind the electric field potential and strength at the center of a hemisphere of radius R charged uniformly with the the surface density σ.
View SolutionA uniform rectangular thin sheet ABCD of mass M has length a and breadth b, as shown in the figure. If the shaded portion HBGO is cut-off, the coordinates of the center of mass of the remaining portion will be:

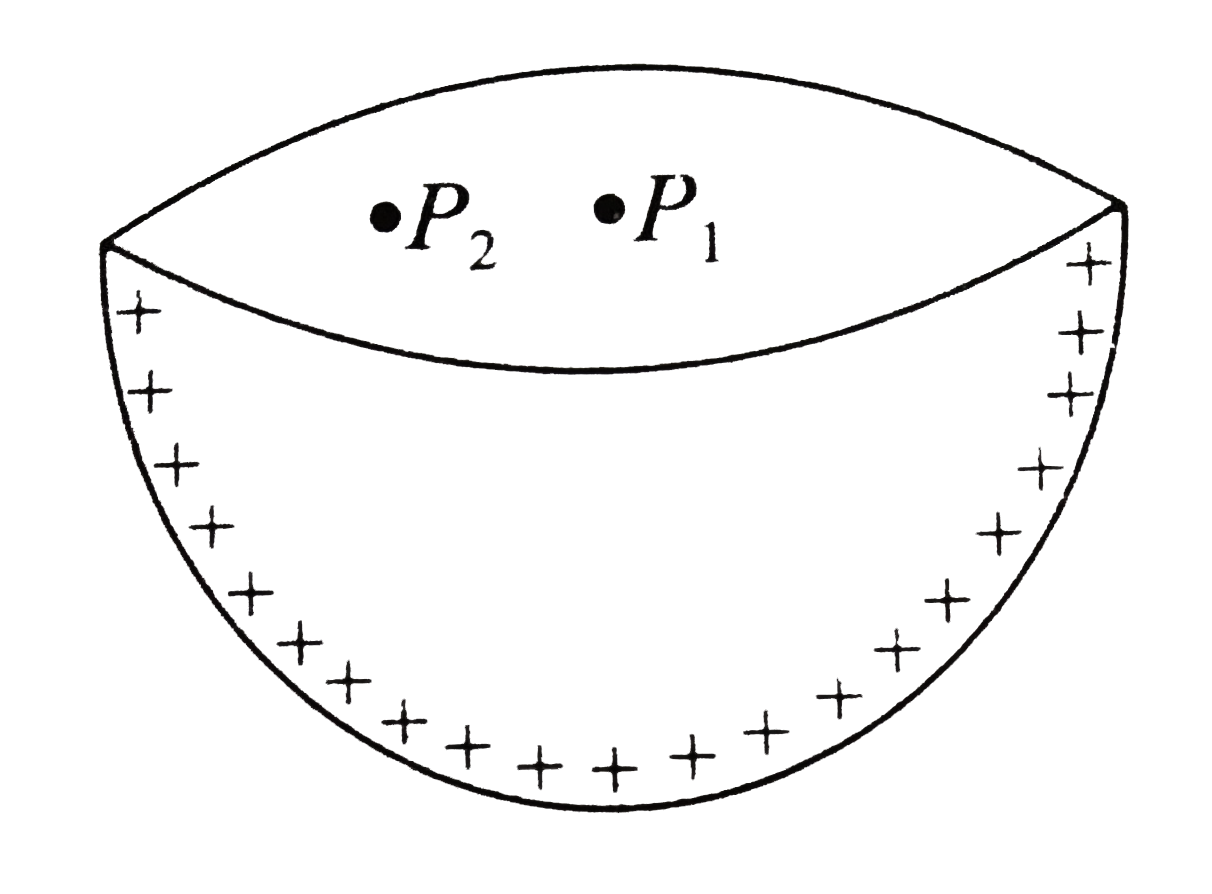
View SolutionConsider a uniformly charged hemispherical shell shown in figure. Indicate the directions (not magnitude) of the electric field at the central point P1 and an off-center point P2 on the drum-head of the shell.
View Solution