An iron tyre is to be fitted onto a wooden wheel 1.0 m in diameter. The diameter of the tyre is 6 mm smaller than that of wheel the tyre should be heated so that its temperature increases by a minimum of (coefficient of volume expansion of iron is 3.6×10−5/∘C)
167∘C
334∘C
500∘C
1000∘C
The correct Answer is:C
To solve the problem of fitting an iron tyre onto a wooden wheel, we need to determine the minimum temperature increase required for the tyre to fit properly. Here’s a step-by-step solution:
Step 1: Identify the diameters
The diameter of the wooden wheel is given as 1.0 m. To convert this to millimeters:
Diameter of the wheel=1.0m=1000mm
The diameter of the tyre is 6 mm smaller than that of the wheel:
Diameter of the tyre=1000mm−6mm=994mm
Step 2: Calculate the radius of the tyre
The radius of the tyre can be calculated as:
Radius of the tyre=Diameter of the tyre2=994mm2=497mm
Step 3: Determine the change in diameter required
To fit the tyre onto the wheel, we need to increase the diameter of the tyre by 6 mm. Therefore, the change in diameter (ΔD) is:
ΔD=6mm
Step 4: Calculate the change in radius
The change in radius (Δr) is half of the change in diameter:
Δr=ΔD2=6mm2=3mm
Step 5: Relate the change in radius to temperature change
The change in radius due to thermal expansion can be expressed as:
Δr=r⋅α⋅ΔT
where:
- r is the original radius (497 mm),
- α is the coefficient of linear expansion (which is γ3 for volume expansion, where γ=3.6×10−5°C−1),
- ΔT is the change in temperature.
Step 6: Substitute the values
First, calculate α:
α=γ3=3.6×10−53=1.2×10−5°C−1
Now substitute into the equation:
3mm=497mm⋅(1.2×10−5°C−1)⋅ΔT
Step 7: Solve for ΔT
Rearranging the equation gives:
ΔT=3mm497mm⋅1.2×10−5°C−1
Calculating this:
ΔT=3497⋅1.2×10−5≈35.964×10−3≈502.5°C
Final Answer
The minimum temperature increase required for the iron tyre to fit onto the wooden wheel is approximately:
ΔT≈500°C
The diameter of the wooden wheel is given as 1.0 m. To convert this to millimeters:
Diameter of the wheel=1.0m=1000mm
Diameter of the tyre=1000mm−6mm=994mm
The radius of the tyre can be calculated as:
Radius of the tyre=Diameter of the tyre2=994mm2=497mm
To fit the tyre onto the wheel, we need to increase the diameter of the tyre by 6 mm. Therefore, the change in diameter (ΔD) is:
ΔD=6mm
The change in radius (Δr) is half of the change in diameter:
Δr=ΔD2=6mm2=3mm
The change in radius due to thermal expansion can be expressed as:
Δr=r⋅α⋅ΔT
where:
- r is the original radius (497 mm),
- α is the coefficient of linear expansion (which is γ3 for volume expansion, where γ=3.6×10−5°C−1),
- ΔT is the change in temperature.
First, calculate α:
α=γ3=3.6×10−53=1.2×10−5°C−1
3mm=497mm⋅(1.2×10−5°C−1)⋅ΔT
Rearranging the equation gives:
ΔT=3mm497mm⋅1.2×10−5°C−1
ΔT=3497⋅1.2×10−5≈35.964×10−3≈502.5°C
The minimum temperature increase required for the iron tyre to fit onto the wooden wheel is approximately:
ΔT≈500°C
टॉपर्स ने हल किए ये सवाल
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Video
समान प्रश्न
Due to thermal expansion with rise in temperature:
View SolutionA body cools in a surrounding of constant temperature 30∘C Its heat capacity is 2J/∘C. Initial temperature of cooling is valid. The body of mass 1 kg cools to 38∘C in 10 min
When the body temperature has reached 38∘C, it is heated again so that it reaches 40∘C in 10 min. The heat required from a heater by the body is
View SolutionA lead ball at 25∘C is dropped from a height of 2 km. It is heated due to air resistance and it is assumed that all of its kinetic energy is used in increasing the temperature of ball. Find the final temperature of the ball.
View SolutionThe displacement of a particle is given by y=(6t2+3t+4)m, where t is in seconds. Calculate the instantaneous speed of the particle.
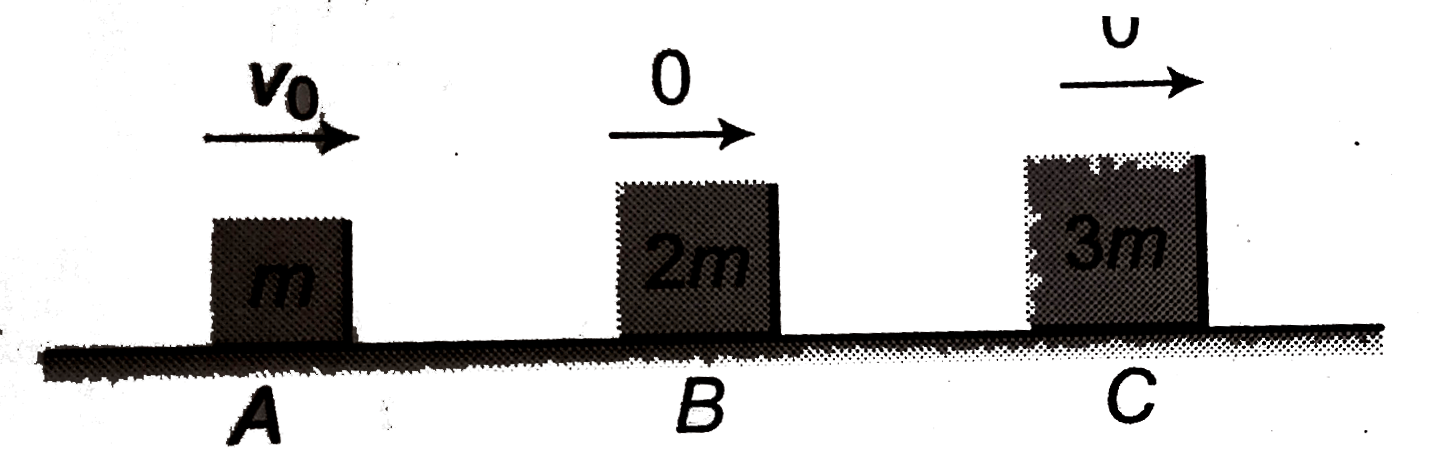
View SolutionThree objects A ,B and C are kept in a straight line on a smooth horizontal surface. These have masses m, 2m and 3m , respectively . The head - on elastic collision takes place between A and B and then B makes completely inelastic collision with C. All motions occur on the same straight line. The final speed of C will be
View SolutionAn iron tyre is to be fitted onto a wooden wheel 1.0 m in diameter. The diameter of the tyre is 6 mm smaller than that of wheel the tyre should be heated so that its temperature increases by a minimum of (coefficient of volume expansion of iron is 3.6xx10^-5//^@C )
View SolutionAn iron tyre of diameter 2 m is to be fitted on to a wooden wheel of diameter 2.01 m. The temperature to which the tyre must be heated , if alpha=11xx10^(-6).^@C^(-1) and room temperature is 20^@C , will be
View SolutionAn iron tyre is to be fitted on a wooden wheel 0.1m in diameter. The miameter of the tyre is 6 mm smaller than that of the wheel. The tyre should be heated by a temperature of (coefficient of volume expansion or iron is 3.6xx10^(-5)//^(@)C )………….. .
View SolutionAn iron wheel has to be fitted into a wooden wheel of 1 meter diameter. The diameter of the tire is 6 mm less than the wooden wheel. If the volume diffusion coefficient of iron 3.6xx10^(-5) //""^@C If the temperature of the tire is increased by a minimum of how many degrees Celsius?
View SolutionAn iron tyre is to be fitted onto a wooden wheel 1m in diameter. The diameter of the tyre is 5 mm smaller than wheel. How much should the temperature of the tyre be increased for this purpose? alpha for iron = 12 xx 10^(-6) per celsius degree.
View SolutionAn iron ring 1.20 m in diameter is to be put on a wooden cart wheel. The diameter of this wheel is 1.0 cm greater than that of the ring. The temperature of the ring that must be raised before it slips on the wooden wheel is (Coefficient of linear expansion of iron = 12 xx 10^(-6)//^(@) C ).
View SolutionA steel tyre of 1.2 m inner diameter at 20∘C is to be fitted on a cartwheel of 120.33 cm diameter of the tyre. Calculate the temperature to which the steel tyre is to be raised so that it will just slip on the wheel.(αSteel=11×10−6/∘C)
View SolutionHow is the tyre of iron of a bullock cart so tightly fitted to the wooden wheel ?
View SolutionIron tyres are mounted on the wooden wheels of a tonga. Initially the diameter of the iron tyre is:
View SolutionWhy is the diameter of an iron tyre kept slightly smaller than the wooden wheel on which this tyre is to be mounted? Explain.
View Solution

