find the minimum attainable pressure of an ideal gs in the process T=t0+∝V2, where T0n and α are positive constants and (V) is the volume of one mole of gas.
Given,
T=T0+αV2 (i)
For 1 mol of a gas, PV=RT
or V=RTP
Substituting this value in Eq. (i) we get
T=T0+α(RTP)2=T0+αR2T2P2
or TP2=T0P2+αR2T2
or P=√αRT(T−T0)−1/2
After differenating, we get
dPdT=√αR[(T−T0)−1/212T(T−T0)−3/2]
For minimum pressure,
dPdT=0
∴0=√αR[(T−T0)−1/212T(T−T0)−3/2]
After solving, T=2T0
Form Eq. (ii),
Pmin=√αR2T0(2T0−T0)−3/2
=2R√αT0
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Single Correct
140 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
28 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.2
28 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
The temperature of a gas is raised while its volume remains constant, the pressure exerted by the gas on the walls of the container increases because its molecules
View SolutionFor an ideal gas
View SolutionExplain why the temperature of a gas drops in an adiabatic expansion, on basis of the kinetic theory of gases,
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
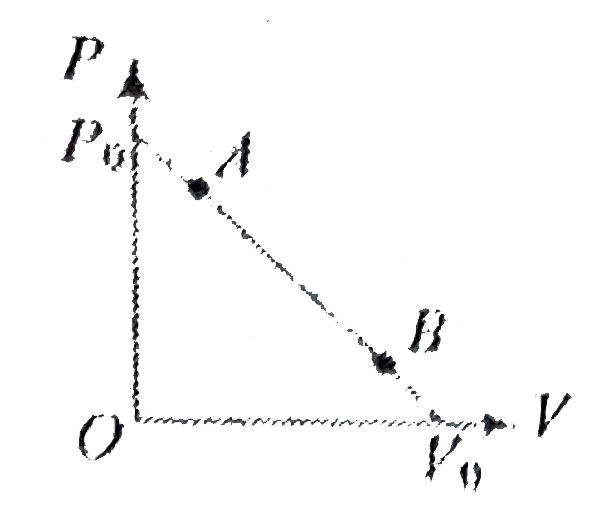
The absolute temperature T versus volume V for the given process is
View SolutionThe period of a simple pendulum whose bob is hollow metallic sphere is T. The period is T1 when the bob is filled with sand, T2 where it is filled with mercury and T3 when it is half filled with mercury Which of the following is true?
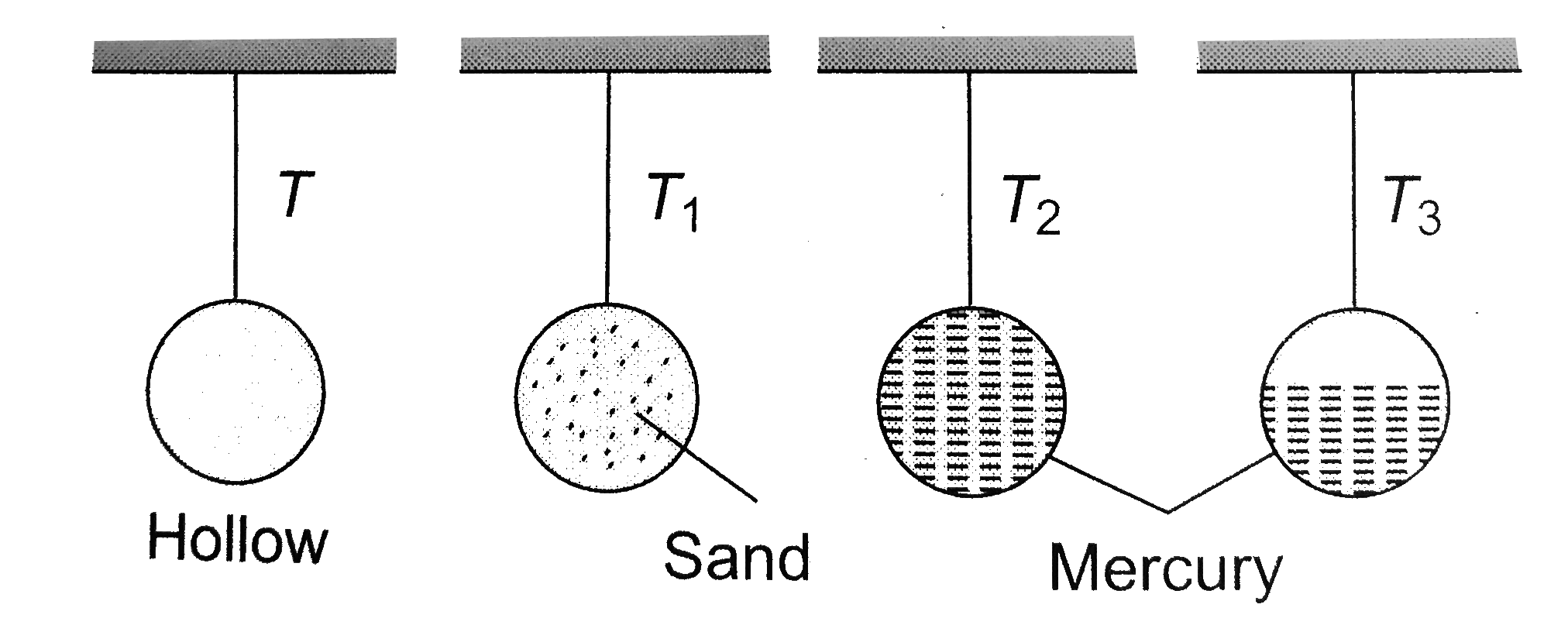
View Solutionfind the minimum attainable pressure of an ideal gs in the process T = t_0 + prop V^2 , where T_(0)n and alpha are positive constants and (V) is the volume of one mole of gas.
View SolutionFind the minimum attainable pressure of an ideal gas in the process T = T_(0) + alpha V^(2) , Where T_(0) and alpha are positive constant and V is the volume of one mole of gas. Draw the approximate T -V plot of this process.
View SolutionOne mole of an ideal gas undergoes a process in which T=T0+aV3, where T0 and a are positive constants and V is molar volume. The volume for which pressure with be minimum is
View SolutionFind the minimum attainable pressure of ideal gas in the process T = T_0 + alpha V^2 , where T_0 and alpha positive constants, and V is the volume of one mole of gas. Draw the approximate p vs V plot of this process.
View SolutionFind the minimum attainabel pressure of one mole of an ideal gas. If during its expansion its temprature and volume are related as T=T0+αV2 where T0&α are positive constants
View SolutionThe temperature (T) of one mole of an ideal gas varies with its volume (V) as T= - alpha V^(3) + beta V^(2) , where alpha and beta are positive constants. The maximum pressure of gas during this process is
View SolutionFind the minimum attainable pressure of one mole of an ideal gas, if during its expansion its temperature and volume are related as T=T0+αV2 where T0andα are positive constants.
View SolutionIf the minimum attainable pressure of ideal gas in the process T=T0+αV2 where T, and α are positive constants and V is the volume of one mole of gas is √NR2αT0 where N is an integer. Then N is equal to
View SolutionFind the minimum attainable pressure of one mole of an ideal gas if during its expansion its temperature and volume are related as T=T_(0)+alphaV^(2) where T_(0)" and "alpha are positive constants.
View SolutionOne mole of an ideal gas with heat capacity at constant pressure C_p undergoes the process T=T_0 + alpha V, where T_0 and ' alpha ' are constant. Find heat capacity of the gas as function of its volume,
View SolutionFind the minimum attainable pressure of one mole of an ideal gas, if during its expansion its temperature and volume are related as T = T_(0) + alpha V^(2) where T_(0) and alpha are positive constants.
View Solution

